From Fairness to Infinity: Outcome-Indistinguishable (Omni)Prediction in Evolving Graphs

Professional networks provide invaluable entree to opportunity through referrals and introductions. A rich literature shows they also serve to entrench and even exacerbate a status quo of privilege and disadvantage. Hiring platforms, equipped with the ability to nudge link formation, provide a tantalizing opening for beneficial structural change. We anticipate that key to this prospect will be the ability to estimate the likelihood of edge formation in an evolving graph. Outcome-indistinguishable prediction algorithms ensure that the modeled world is indistinguishable from the real world by a family of statistical tests. Omnipredictors ensure that predictions can be post-processed to yield loss minimization competitive with respect to a benchmark class of predictors for many losses simultaneously, with appropriate post-processing. We begin by observing that, by combining a slightly modified form of the online K29 star algorithm of Vovk (2007) with basic facts from the theory of reproducing kernel Hilbert spaces, one can derive simple and efficient online algorithms satisfying outcome indistinguishability and omniprediction, with guarantees that improve upon, or are complementary to, those currently known. This is of independent interest. We apply these techniques to evolving graphs, obtaining online outcome-indistinguishable omnipredictors for rich -- possibly infinite -- sets of distinguishers that capture properties of pairs of nodes, and their neighborhoods. This yields, inter alia, multicalibrated predictions of edge formation with respect to pairs of demographic groups, and the ability to simultaneously optimize loss as measured by a variety of social welfare functions.

Large Scale Transfer Learning for Tabular Data via Language Modeling

Tabular data -- structured, heterogeneous, spreadsheet-style data with rows and columns -- is widely used in practice across many domains. However, while recent foundation models have reduced the need for developing task-specific datasets and predictors in domains such as language modeling and computer vision, this transfer learning paradigm has not had similar impact in the tabular domain. In this work, we seek to narrow this gap and present TabuLa-8B, a language model for tabular prediction. We define a process for extracting a large, high-quality training dataset from the TabLib corpus, proposing methods for tabular data filtering and quality control. Using the resulting dataset, which comprises over 1.6B rows from 3.1M unique tables, we fine-tune a Llama 3-8B large language model (LLM) for tabular data prediction (classification and binned regression) using a novel packing and attention scheme for tabular prediction. Through evaluation across a test suite of 329 datasets, we find that TabuLa-8B has zero-shot accuracy on unseen tables that is over 15 percentage points (pp) higher than random guessing, a feat that is not possible with existing state-of-the-art tabular prediction models (e.g. XGBoost, TabPFN). In the few-shot setting (1-32 shots), without any fine-tuning on the target datasets, TabuLa-8B is 5-15 pp more accurate than XGBoost and TabPFN models that are explicitly trained on equal, or even up to 16x more data. We release our model, code, and data along with the publication of this paper.

Insufficient Statistics Perturbation: Stable Estimators for Private Least Squares

We present a sample- and time-efficient differentially private algorithm for ordinary least squares, with error that depends linearly on the dimension and is independent of the condition number of $X^\top X$, where $X$ is the design matrix. All prior private algorithms for this task require either $d^{3/2}$ examples, error growing polynomially with the condition number, or exponential time. Our near-optimal accuracy guarantee holds for any dataset with bounded statistical leverage and bounded residuals. Technically, we build on the approach of Brown et al. (2023) for private mean estimation, adding scaled noise to a carefully designed stable nonprivate estimator of the empirical regression vector.

Difficult Lessons on Social Prediction from Wisconsin Public Schools

Early warning systems (EWS) are prediction algorithms that have recently taken a central role in efforts to improve graduation rates in public schools across the US. These systems assist in targeting interventions at individual students by predicting which students are at risk of dropping out. Despite significant investments and adoption, there remain significant gaps in our understanding of the efficacy of EWS. In this work, we draw on nearly a decade's worth of data from a system used throughout Wisconsin to provide the first large-scale evaluation of the long-term impact of EWS on graduation outcomes. We present evidence that risk assessments made by the prediction system are highly accurate, including for students from marginalized backgrounds. Despite the system's accuracy and widespread use, we find no evidence that it has led to improved graduation rates. We surface a robust statistical pattern that can explain why these seemingly contradictory insights hold. Namely, environmental features, measured at the level of schools, contain significant signal about dropout risk. Within each school, however, academic outcomes are essentially independent of individual student performance. This empirical observation indicates that assigning all students within the same school the same probability of graduation is a nearly optimal prediction. Our work provides an empirical backbone for the robust, qualitative understanding among education researchers and policy-makers that dropout is structurally determined. The primary barrier to improving outcomes lies not in identifying students at risk of dropping out within specific schools, but rather in overcoming structural differences across different school districts. Our findings indicate that we should carefully evaluate the decision to fund early warning systems without also devoting resources to interventions tackling structural barriers.

Making Decisions under Outcome Performativity

Decision-makers often act in response to data-driven predictions, with the goal of achieving favorable outcomes. In such settings, predictions don't passively forecast the future; instead, predictions actively shape the distribution of outcomes they are meant to predict. This performative prediction setting raises new challenges for learning "optimal" decision rules. In particular, existing solution concepts do not address the apparent tension between the goals of forecasting outcomes accurately and steering individuals to achieve desirable outcomes. To contend with this concern, we introduce a new optimality concept -- performative omniprediction -- adapted from the supervised (non-performative) learning setting. A performative omnipredictor is a single predictor that simultaneously encodes the optimal decision rule with respect to many possibly-competing objectives. Our main result demonstrates that efficient performative omnipredictors exist, under a natural restriction of performative prediction, which we call outcome performativity. On a technical level, our results follow by carefully generalizing the notion of outcome indistinguishability to the outcome performative setting. From an appropriate notion of Performative OI, we recover many consequences known to hold in the supervised setting, such as omniprediction and universal adaptability.

A Sharp Characterization of Linear Estimators for Offline Policy Evaluation

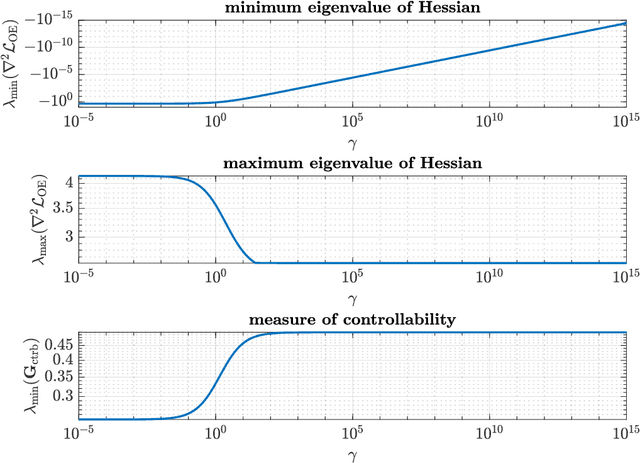
Offline policy evaluation is a fundamental statistical problem in reinforcement learning that involves estimating the value function of some decision-making policy given data collected by a potentially different policy. In order to tackle problems with complex, high-dimensional observations, there has been significant interest from theoreticians and practitioners alike in understanding the possibility of function approximation in reinforcement learning. Despite significant study, a sharp characterization of when we might expect offline policy evaluation to be tractable, even in the simplest setting of linear function approximation, has so far remained elusive, with a surprising number of strong negative results recently appearing in the literature. In this work, we identify simple control-theoretic and linear-algebraic conditions that are necessary and sufficient for classical methods, in particular Fitted Q-iteration (FQI) and least squares temporal difference learning (LSTD), to succeed at offline policy evaluation. Using this characterization, we establish a precise hierarchy of regimes under which these estimators succeed. We prove that LSTD works under strictly weaker conditions than FQI. Furthermore, we establish that if a problem is not solvable via LSTD, then it cannot be solved by a broad class of linear estimators, even in the limit of infinite data. Taken together, our results provide a complete picture of the behavior of linear estimators for offline policy evaluation (OPE), unify previously disparate analyses of canonical algorithms, and provide significantly sharper notions of the underlying statistical complexity of OPE.

Globally Convergent Policy Search over Dynamic Filters for Output Estimation

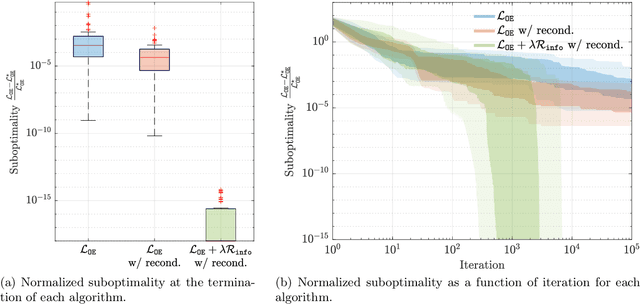
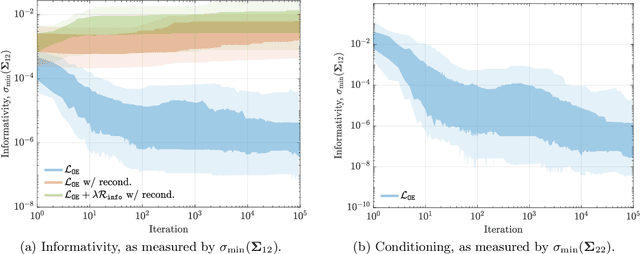
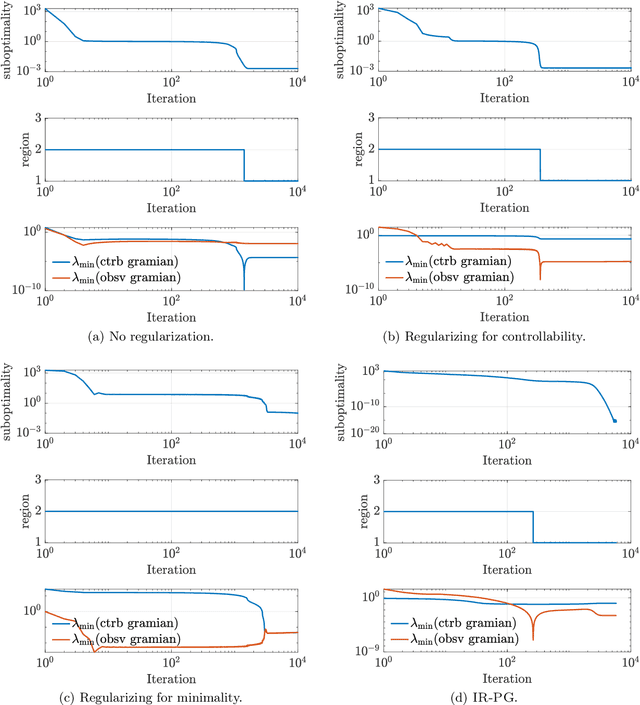
We introduce the first direct policy search algorithm which provably converges to the globally optimal $\textit{dynamic}$ filter for the classical problem of predicting the outputs of a linear dynamical system, given noisy, partial observations. Despite the ubiquity of partial observability in practice, theoretical guarantees for direct policy search algorithms, one of the backbones of modern reinforcement learning, have proven difficult to achieve. This is primarily due to the degeneracies which arise when optimizing over filters that maintain internal state. In this paper, we provide a new perspective on this challenging problem based on the notion of $\textit{informativity}$, which intuitively requires that all components of a filter's internal state are representative of the true state of the underlying dynamical system. We show that informativity overcomes the aforementioned degeneracy. Specifically, we propose a $\textit{regularizer}$ which explicitly enforces informativity, and establish that gradient descent on this regularized objective - combined with a ``reconditioning step'' - converges to the globally optimal cost a $\mathcal{O}(1/T)$ rate. Our analysis relies on several new results which may be of independent interest, including a new framework for analyzing non-convex gradient descent via convex reformulation, and novel bounds on the solution to linear Lyapunov equations in terms of (our quantitative measure of) informativity.

Stabilizing Dynamical Systems via Policy Gradient Methods

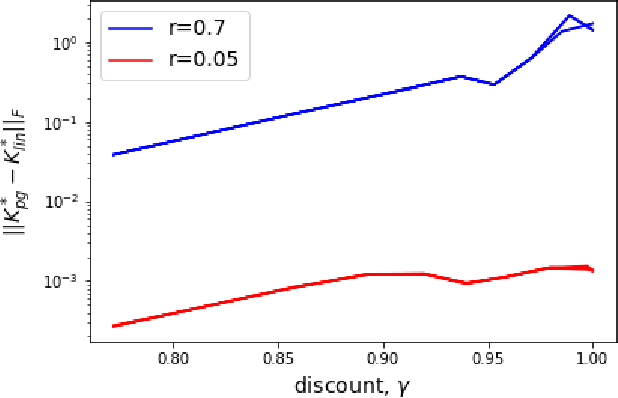
Stabilizing an unknown control system is one of the most fundamental problems in control systems engineering. In this paper, we provide a simple, model-free algorithm for stabilizing fully observed dynamical systems. While model-free methods have become increasingly popular in practice due to their simplicity and flexibility, stabilization via direct policy search has received surprisingly little attention. Our algorithm proceeds by solving a series of discounted LQR problems, where the discount factor is gradually increased. We prove that this method efficiently recovers a stabilizing controller for linear systems, and for smooth, nonlinear systems within a neighborhood of their equilibria. Our approach overcomes a significant limitation of prior work, namely the need for a pre-given stabilizing control policy. We empirically evaluate the effectiveness of our approach on common control benchmarks.

Towards a Dimension-Free Understanding of Adaptive Linear Control

We study the problem of adaptive control of the linear quadratic regulator for systems in very high, or even infinite dimension. We demonstrate that while sublinear regret requires finite dimensional inputs, the ambient state dimension of the system need not be bounded in order to perform online control. We provide the first regret bounds for LQR which hold for infinite dimensional systems, replacing dependence on ambient dimension with more natural notions of problem complexity. Our guarantees arise from a novel perturbation bound for certainty equivalence which scales with the prediction error in estimating the system parameters, without requiring consistent parameter recovery in more stringent measures like the operator norm. When specialized to finite dimensional settings, our bounds recover near optimal dimension and time horizon dependence.

Outside the Echo Chamber: Optimizing the Performative Risk

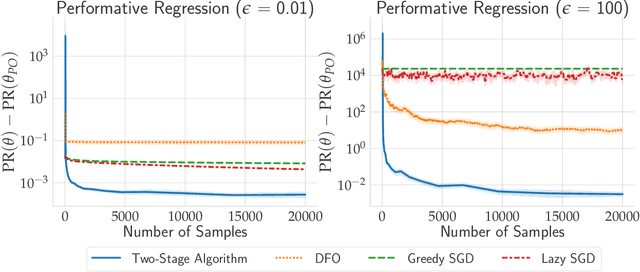
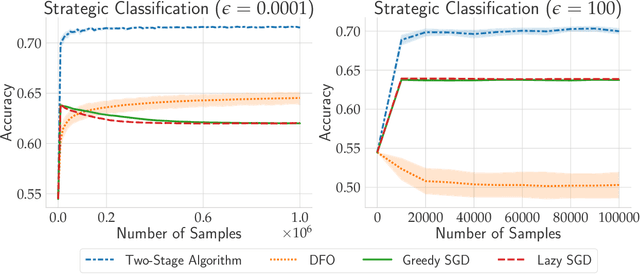
In performative prediction, predictions guide decision-making and hence can influence the distribution of future data. To date, work on performative prediction has focused on finding performatively stable models, which are the fixed points of repeated retraining. However, stable solutions can be far from optimal when evaluated in terms of the performative risk, the loss experienced by the decision maker when deploying a model. In this paper, we shift attention beyond performative stability and focus on optimizing the performative risk directly. We identify a natural set of properties of the loss function and model-induced distribution shift under which the performative risk is convex, a property which does not follow from convexity of the loss alone. Furthermore, we develop algorithms that leverage our structural assumptions to optimize the performative risk with better sample efficiency than generic methods for derivative-free convex optimization.