Learning to Decode the Surface Code with a Recurrent, Transformer-Based Neural Network

Quantum error-correction is a prerequisite for reliable quantum computation. Towards this goal, we present a recurrent, transformer-based neural network which learns to decode the surface code, the leading quantum error-correction code. Our decoder outperforms state-of-the-art algorithmic decoders on real-world data from Google's Sycamore quantum processor for distance 3 and 5 surface codes. On distances up to 11, the decoder maintains its advantage on simulated data with realistic noise including cross-talk, leakage, and analog readout signals, and sustains its accuracy far beyond the 25 cycles it was trained on. Our work illustrates the ability of machine learning to go beyond human-designed algorithms by learning from data directly, highlighting machine learning as a strong contender for decoding in quantum computers.

Nonequilibrium Monte Carlo for unfreezing variables in hard combinatorial optimization

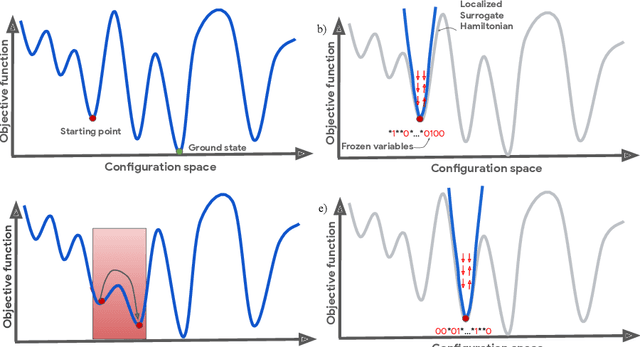
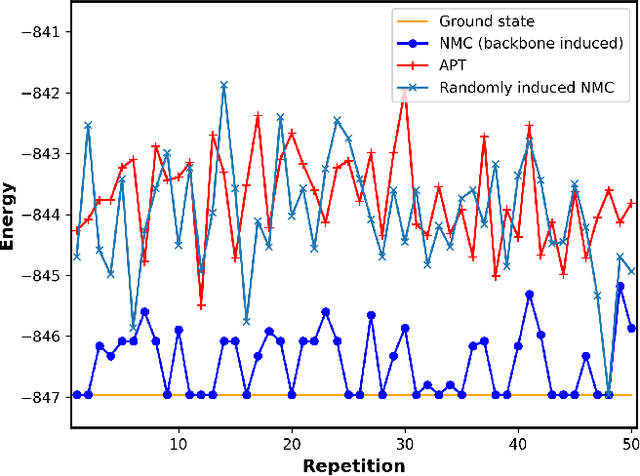
Optimizing highly complex cost/energy functions over discrete variables is at the heart of many open problems across different scientific disciplines and industries. A major obstacle is the emergence of many-body effects among certain subsets of variables in hard instances leading to critical slowing down or collective freezing for known stochastic local search strategies. An exponential computational effort is generally required to unfreeze such variables and explore other unseen regions of the configuration space. Here, we introduce a quantum-inspired family of nonlocal Nonequilibrium Monte Carlo (NMC) algorithms by developing an adaptive gradient-free strategy that can efficiently learn key instance-wise geometrical features of the cost function. That information is employed on-the-fly to construct spatially inhomogeneous thermal fluctuations for collectively unfreezing variables at various length scales, circumventing costly exploration versus exploitation trade-offs. We apply our algorithm to two of the most challenging combinatorial optimization problems: random k-satisfiability (k-SAT) near the computational phase transitions and Quadratic Assignment Problems (QAP). We observe significant speedup and robustness over both specialized deterministic solvers and generic stochastic solvers. In particular, for 90% of random 4-SAT instances we find solutions that are inaccessible for the best specialized deterministic algorithm known as Survey Propagation (SP) with an order of magnitude improvement in the quality of solutions for the hardest 10% instances. We also demonstrate two orders of magnitude improvement in time-to-solution over the state-of-the-art generic stochastic solver known as Adaptive Parallel Tempering (APT).

Power of data in quantum machine learning

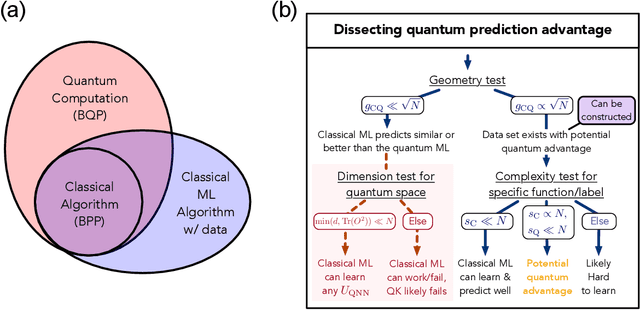
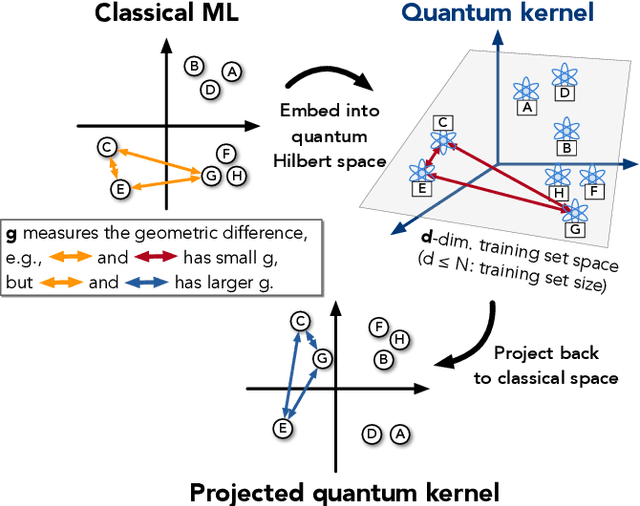
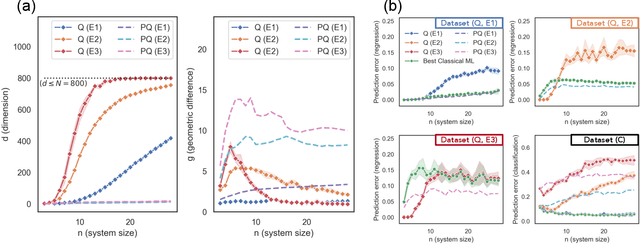
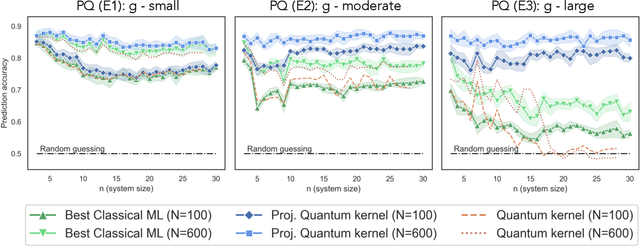
The use of quantum computing for machine learning is among the most exciting prospective applications of quantum technologies. At the crux of excitement is the potential for quantum computers to perform some computations exponentially faster than their classical counterparts. However, a machine learning task where some data is provided can be considerably different than more commonly studied computational tasks. In this work, we show that some problems that are classically hard to compute can be predicted easily with classical machines that learn from data. We find that classical machines can often compete or outperform existing quantum models even on data sets generated by quantum evolution, especially at large system sizes. Using rigorous prediction error bounds as a foundation, we develop a methodology for assessing the potential for quantum advantage in prediction on learning tasks. We show how the use of exponentially large quantum Hilbert space in existing quantum models can result in significantly inferior prediction performance compared to classical machines. To circumvent the observed setbacks, we propose an improvement by projecting all quantum states to an approximate classical representation. The projected quantum model provides a simple and rigorous quantum speed-up for a recently proposed learning problem in the fault-tolerant regime. For more near-term quantum models, the projected versions demonstrate a significant prediction advantage over some classical models on engineered data sets in one of the largest numerical tests for gate-based quantum machine learning to date, up to 30 qubits.

Learnability and Complexity of Quantum Samples

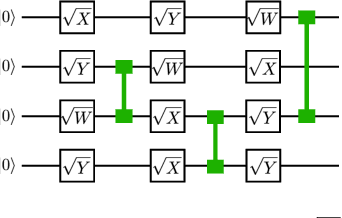
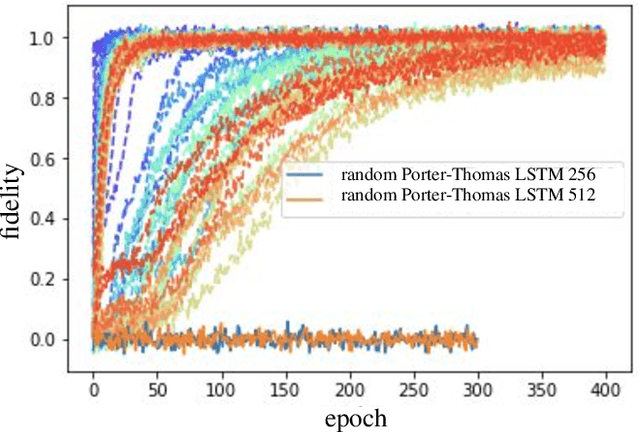
Given a quantum circuit, a quantum computer can sample the output distribution exponentially faster in the number of bits than classical computers. A similar exponential separation has yet to be established in generative models through quantum sample learning: given samples from an n-qubit computation, can we learn the underlying quantum distribution using models with training parameters that scale polynomial in n under a fixed training time? We study four kinds of generative models: Deep Boltzmann machine (DBM), Generative Adversarial Networks (GANs), Long Short-Term Memory (LSTM) and Autoregressive GAN, on learning quantum data set generated by deep random circuits. We demonstrate the leading performance of LSTM in learning quantum samples, and thus the autoregressive structure present in the underlying quantum distribution from random quantum circuits. Both numerical experiments and a theoretical proof in the case of the DBM show exponentially growing complexity of learning-agent parameters required for achieving a fixed accuracy as n increases. Finally, we establish a connection between learnability and the complexity of generative models by benchmarking learnability against different sets of samples drawn from probability distributions of variable degrees of complexities in their quantum and classical representations.

TensorFlow Quantum: A Software Framework for Quantum Machine Learning

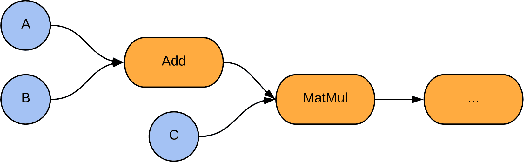
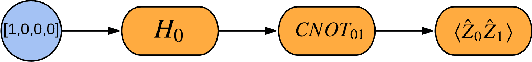
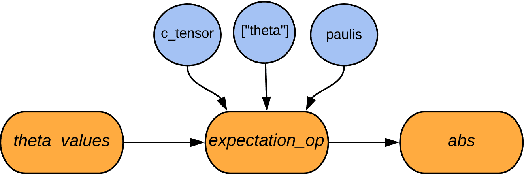
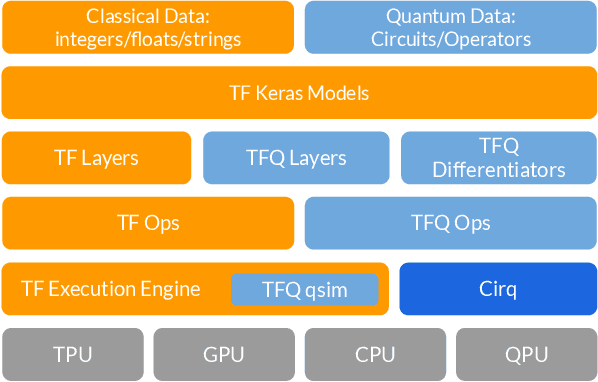
We introduce TensorFlow Quantum (TFQ), an open source library for the rapid prototyping of hybrid quantum-classical models for classical or quantum data. This framework offers high-level abstractions for the design and training of both discriminative and generative quantum models under TensorFlow and supports high-performance quantum circuit simulators. We provide an overview of the software architecture and building blocks through several examples and review the theory of hybrid quantum-classical neural networks. We illustrate TFQ functionalities via several basic applications including supervised learning for quantum classification, quantum control, and quantum approximate optimization. Moreover, we demonstrate how one can apply TFQ to tackle advanced quantum learning tasks including meta-learning, Hamiltonian learning, and sampling thermal states. We hope this framework provides the necessary tools for the quantum computing and machine learning research communities to explore models of both natural and artificial quantum systems, and ultimately discover new quantum algorithms which could potentially yield a quantum advantage.

Learning Non-Markovian Quantum Noise from Moiré-Enhanced Swap Spectroscopy with Deep Evolutionary Algorithm

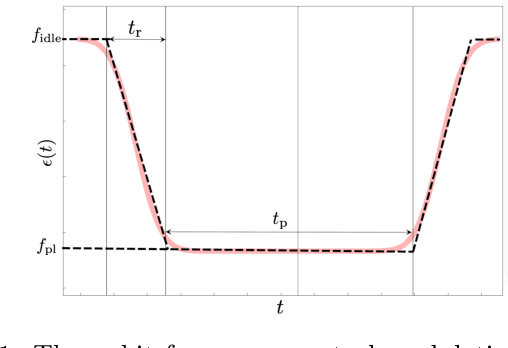
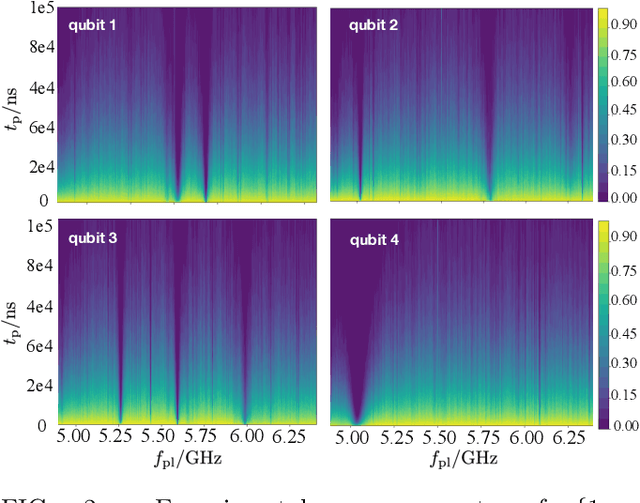
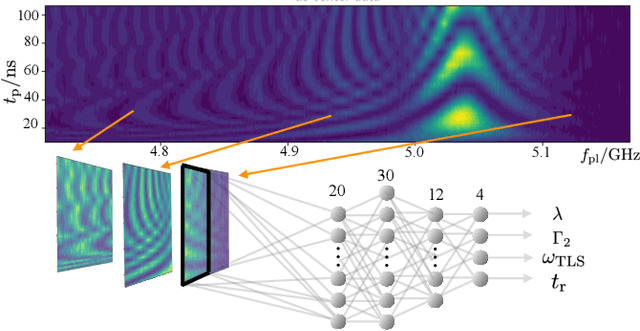
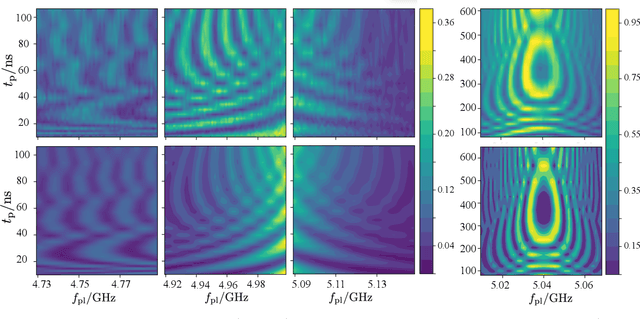
Two-level-system (TLS) defects in amorphous dielectrics are a major source of noise and decoherence in solid-state qubits. Gate-dependent non-Markovian errors caused by TLS-qubit coupling are detrimental to fault-tolerant quantum computation and have not been rigorously treated in the existing literature. In this work, we derive the non-Markovian dynamics between TLS and qubits during a SWAP-like two-qubit gate and the associated average gate fidelity for frequency-tunable Transmon qubits. This gate dependent error model facilitates using qubits as sensors to simultaneously learn practical imperfections in both the qubit's environment and control waveforms. We combine the-state-of-art machine learning algorithm with Moir\'{e}-enhanced swap spectroscopy to achieve robust learning using noisy experimental data. Deep neural networks are used to represent the functional map from experimental data to TLS parameters and are trained through an evolutionary algorithm. Our method achieves the highest learning efficiency and robustness against experimental imperfections to-date, representing an important step towards in-situ quantum control optimization over environmental and control defects.

Barren plateaus in quantum neural network training landscapes

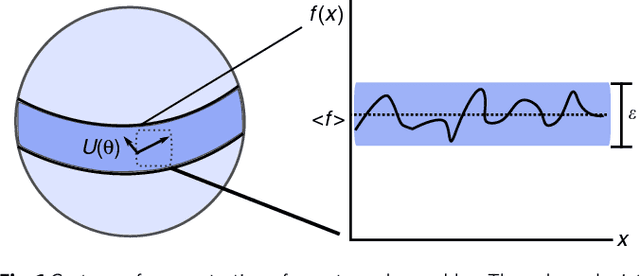
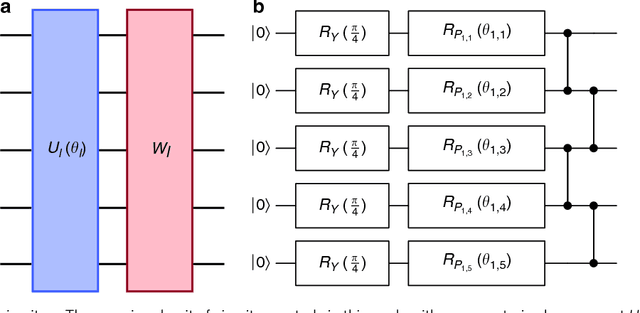
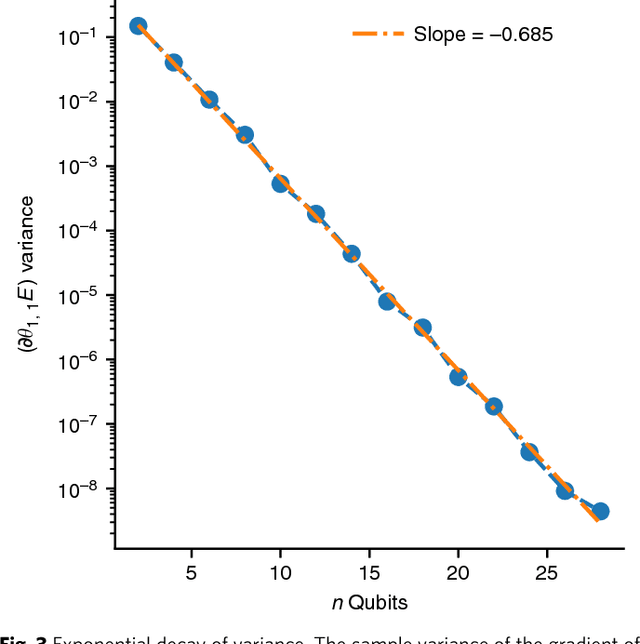
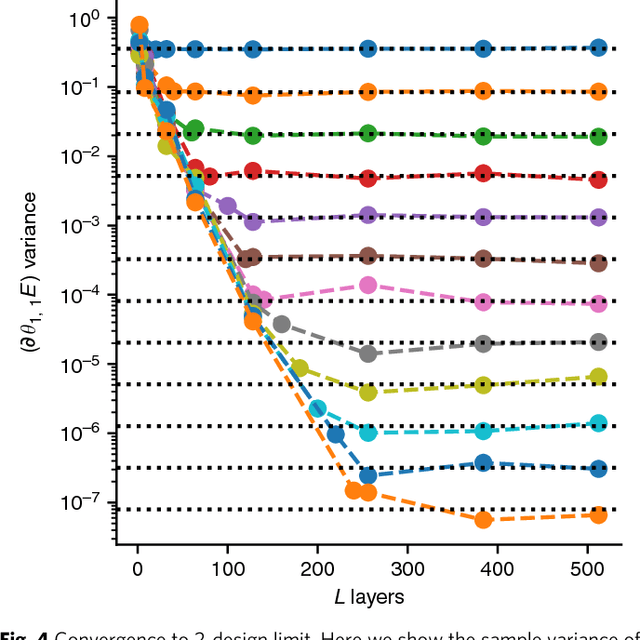
Many experimental proposals for noisy intermediate scale quantum devices involve training a parameterized quantum circuit with a classical optimization loop. Such hybrid quantum-classical algorithms are popular for applications in quantum simulation, optimization, and machine learning. Due to its simplicity and hardware efficiency, random circuits are often proposed as initial guesses for exploring the space of quantum states. We show that the exponential dimension of Hilbert space and the gradient estimation complexity make this choice unsuitable for hybrid quantum-classical algorithms run on more than a few qubits. Specifically, we show that for a wide class of reasonable parameterized quantum circuits, the probability that the gradient along any reasonable direction is non-zero to some fixed precision is exponentially small as a function of the number of qubits. We argue that this is related to the 2-design characteristic of random circuits, and that solutions to this problem must be studied.