Challenges and Opportunities in Quantum Machine Learning

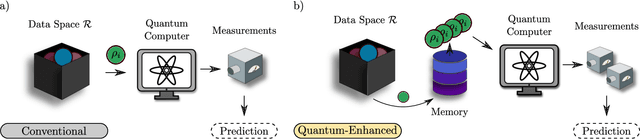
At the intersection of machine learning and quantum computing, Quantum Machine Learning (QML) has the potential of accelerating data analysis, especially for quantum data, with applications for quantum materials, biochemistry, and high-energy physics. Nevertheless, challenges remain regarding the trainability of QML models. Here we review current methods and applications for QML. We highlight differences between quantum and classical machine learning, with a focus on quantum neural networks and quantum deep learning. Finally, we discuss opportunities for quantum advantage with QML.

Provably efficient variational generative modeling of quantum many-body systems via quantum-probabilistic information geometry

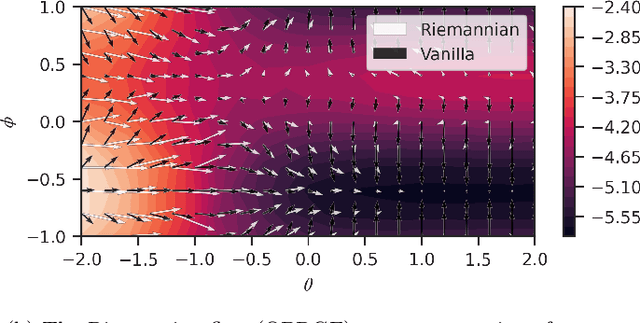
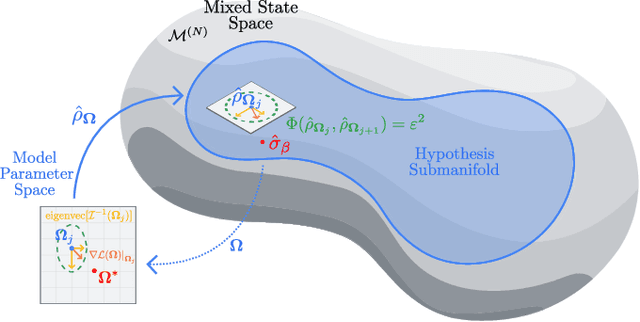
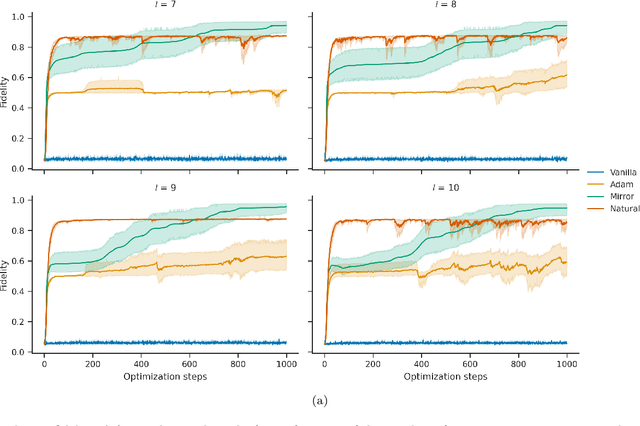
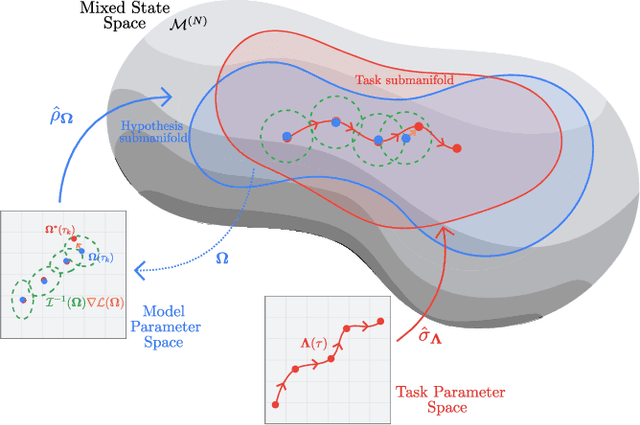
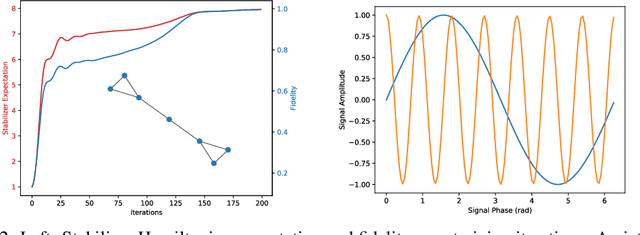
The dual tasks of quantum Hamiltonian learning and quantum Gibbs sampling are relevant to many important problems in physics and chemistry. In the low temperature regime, algorithms for these tasks often suffer from intractabilities, for example from poor sample- or time-complexity. With the aim of addressing such intractabilities, we introduce a generalization of quantum natural gradient descent to parameterized mixed states, as well as provide a robust first-order approximating algorithm, Quantum-Probabilistic Mirror Descent. We prove data sample efficiency for the dual tasks using tools from information geometry and quantum metrology, thus generalizing the seminal result of classical Fisher efficiency to a variational quantum algorithm for the first time. Our approaches extend previously sample-efficient techniques to allow for flexibility in model choice, including to spectrally-decomposed models like Quantum Hamiltonian-Based Models, which may circumvent intractable time complexities. Our first-order algorithm is derived using a novel quantum generalization of the classical mirror descent duality. Both results require a special choice of metric, namely, the Bogoliubov-Kubo-Mori metric. To test our proposed algorithms numerically, we compare their performance to existing baselines on the task of quantum Gibbs sampling for the transverse field Ising model. Finally, we propose an initialization strategy leveraging geometric locality for the modelling of sequences of states such as those arising from quantum-stochastic processes. We demonstrate its effectiveness empirically for both real and imaginary time evolution while defining a broader class of potential applications.

Group-Invariant Quantum Machine Learning

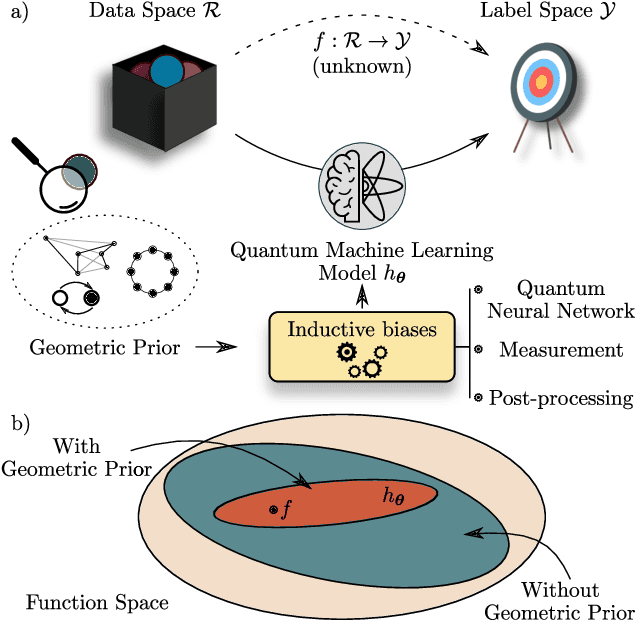
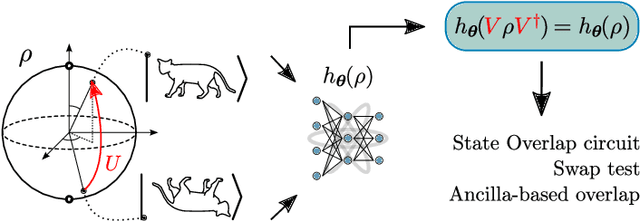
Quantum Machine Learning (QML) models are aimed at learning from data encoded in quantum states. Recently, it has been shown that models with little to no inductive biases (i.e., with no assumptions about the problem embedded in the model) are likely to have trainability and generalization issues, especially for large problem sizes. As such, it is fundamental to develop schemes that encode as much information as available about the problem at hand. In this work we present a simple, yet powerful, framework where the underlying invariances in the data are used to build QML models that, by construction, respect those symmetries. These so-called group-invariant models produce outputs that remain invariant under the action of any element of the symmetry group $\mathfrak{G}$ associated to the dataset. We present theoretical results underpinning the design of $\mathfrak{G}$-invariant models, and exemplify their application through several paradigmatic QML classification tasks including cases when $\mathfrak{G}$ is a continuous Lie group and also when it is a discrete symmetry group. Notably, our framework allows us to recover, in an elegant way, several well known algorithms for the literature, as well as to discover new ones. Taken together, we expect that our results will help pave the way towards a more geometric and group-theoretic approach to QML model design.

A semi-agnostic ansatz with variable structure for quantum machine learning

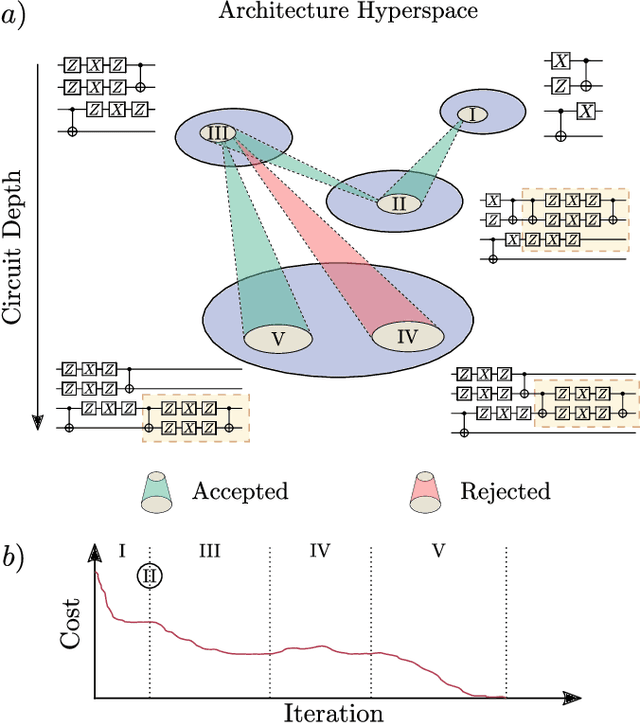
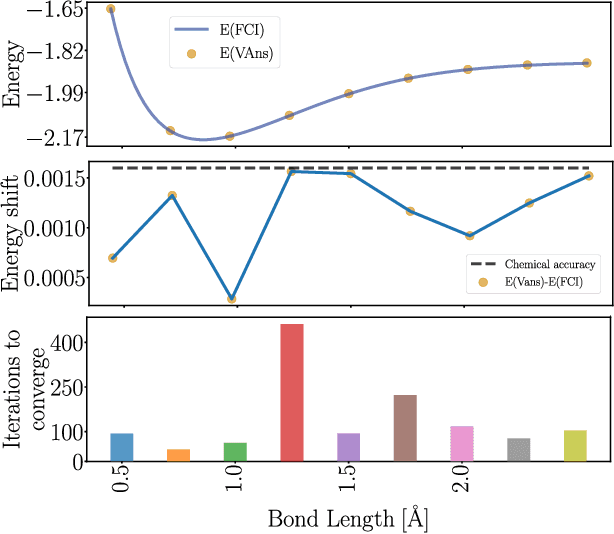
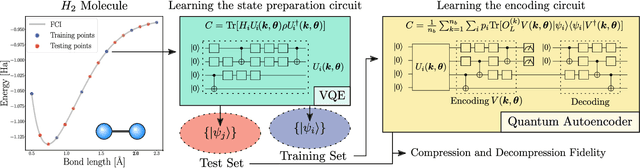
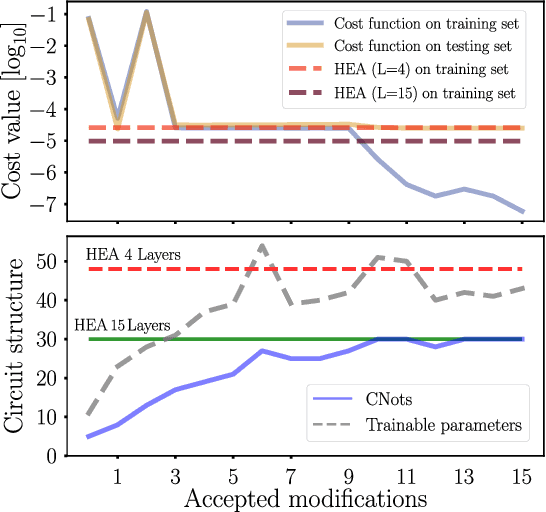
Quantum machine learning (QML) offers a powerful, flexible paradigm for programming near-term quantum computers, with applications in chemistry, metrology, materials science, data science, and mathematics. Here, one trains an ansatz, in the form of a parameterized quantum circuit, to accomplish a task of interest. However, challenges have recently emerged suggesting that deep ansatzes are difficult to train, due to flat training landscapes caused by randomness or by hardware noise. This motivates our work, where we present a variable structure approach to build ansatzes for QML. Our approach, called VAns (Variable Ansatz), applies a set of rules to both grow and (crucially) remove quantum gates in an informed manner during the optimization. Consequently, VAns is ideally suited to mitigate trainability and noise-related issues by keeping the ansatz shallow. We employ VAns in the variational quantum eigensolver for condensed matter and quantum chemistry applications and also in the quantum autoencoder for data compression, showing successful results in all cases.

TensorFlow Quantum: A Software Framework for Quantum Machine Learning

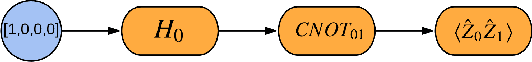
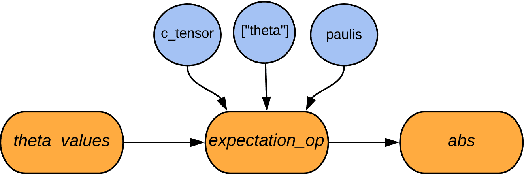
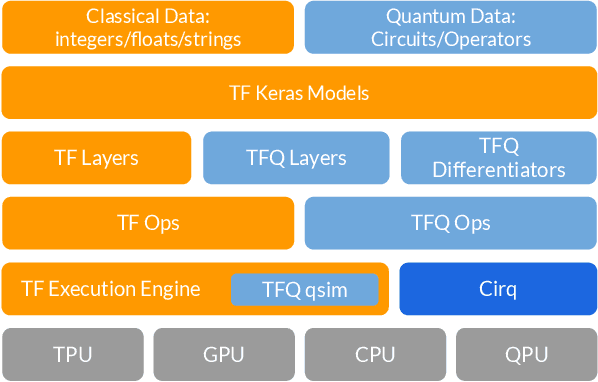
We introduce TensorFlow Quantum (TFQ), an open source library for the rapid prototyping of hybrid quantum-classical models for classical or quantum data. This framework offers high-level abstractions for the design and training of both discriminative and generative quantum models under TensorFlow and supports high-performance quantum circuit simulators. We provide an overview of the software architecture and building blocks through several examples and review the theory of hybrid quantum-classical neural networks. We illustrate TFQ functionalities via several basic applications including supervised learning for quantum classification, quantum control, and quantum approximate optimization. Moreover, we demonstrate how one can apply TFQ to tackle advanced quantum learning tasks including meta-learning, Hamiltonian learning, and sampling thermal states. We hope this framework provides the necessary tools for the quantum computing and machine learning research communities to explore models of both natural and artificial quantum systems, and ultimately discover new quantum algorithms which could potentially yield a quantum advantage.

Quantum Hamiltonian-Based Models and the Variational Quantum Thermalizer Algorithm

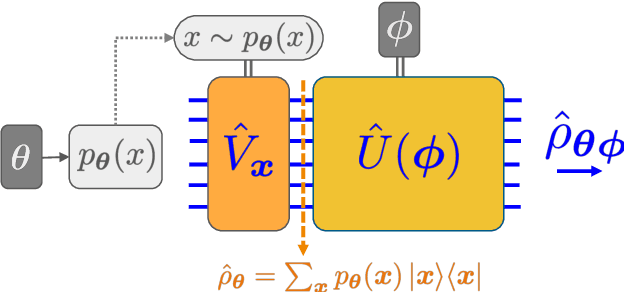
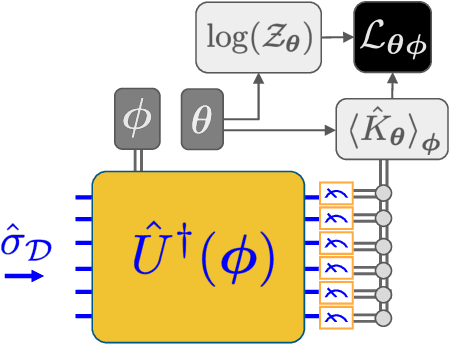
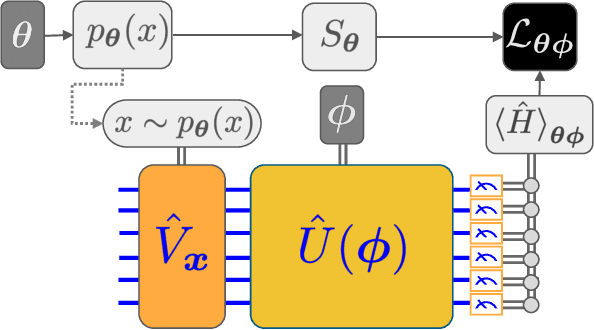
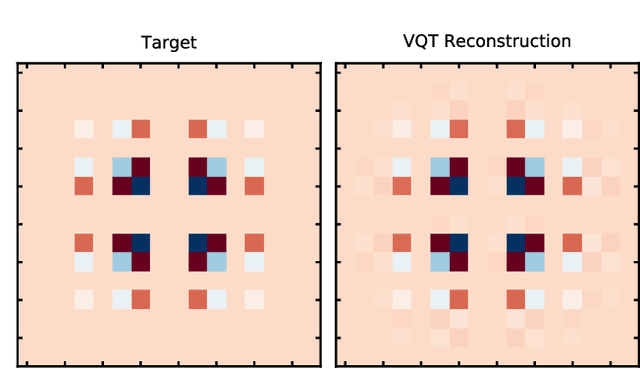
We introduce a new class of generative quantum-neural-network-based models called Quantum Hamiltonian-Based Models (QHBMs). In doing so, we establish a paradigmatic approach for quantum-probabilistic hybrid variational learning, where we efficiently decompose the tasks of learning classical and quantum correlations in a way which maximizes the utility of both classical and quantum processors. In addition, we introduce the Variational Quantum Thermalizer (VQT) for generating the thermal state of a given Hamiltonian and target temperature, a task for which QHBMs are naturally well-suited. The VQT can be seen as a generalization of the Variational Quantum Eigensolver (VQE) to thermal states: we show that the VQT converges to the VQE in the zero temperature limit. We provide numerical results demonstrating the efficacy of these techniques in illustrative examples. We use QHBMs and the VQT on Heisenberg spin systems, we apply QHBMs to learn entanglement Hamiltonians and compression codes in simulated free Bosonic systems, and finally we use the VQT to prepare thermal Fermionic Gaussian states for quantum simulation.

Quantum Graph Neural Networks

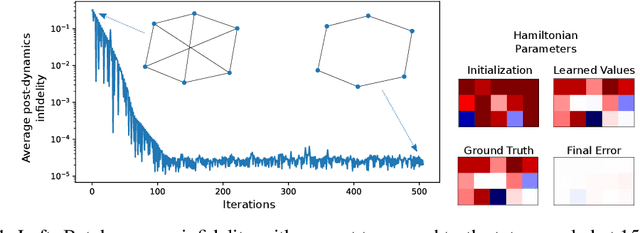
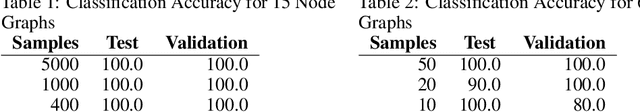
We introduce Quantum Graph Neural Networks (QGNN), a new class of quantum neural network ansatze which are tailored to represent quantum processes which have a graph structure, and are particularly suitable to be executed on distributed quantum systems over a quantum network. Along with this general class of ansatze, we introduce further specialized architectures, namely, Quantum Graph Recurrent Neural Networks (QGRNN) and Quantum Graph Convolutional Neural Networks (QGCNN). We provide four example applications of QGNNs: learning Hamiltonian dynamics of quantum systems, learning how to create multipartite entanglement in a quantum network, unsupervised learning for spectral clustering, and supervised learning for graph isomorphism classification.

Learning to learn with quantum neural networks via classical neural networks

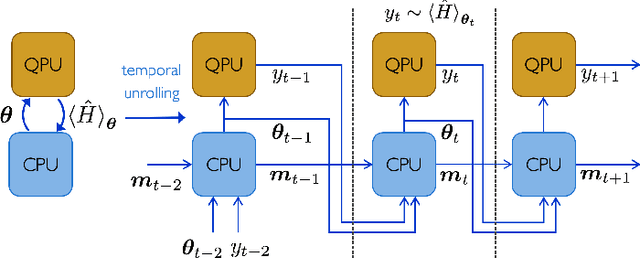
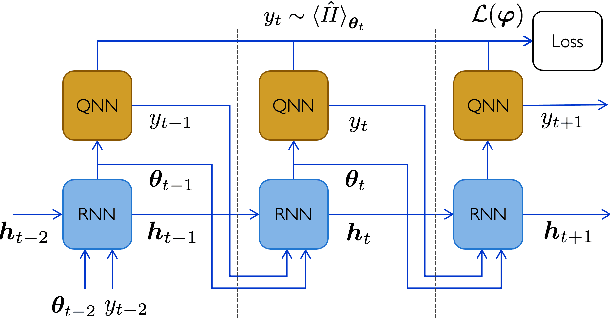
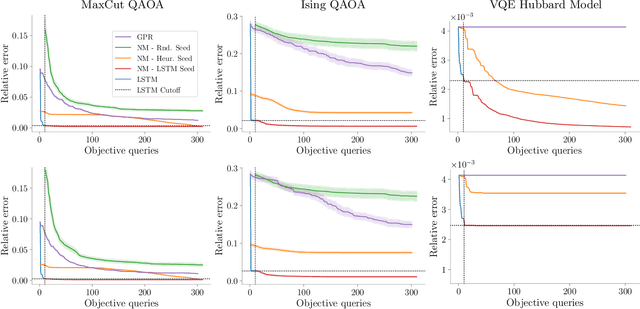
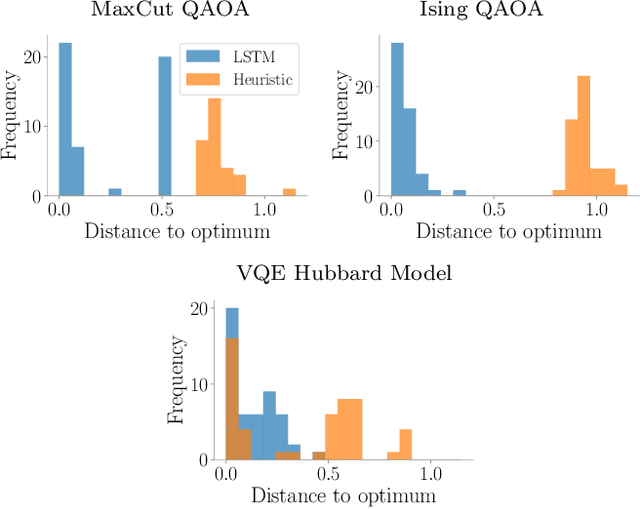
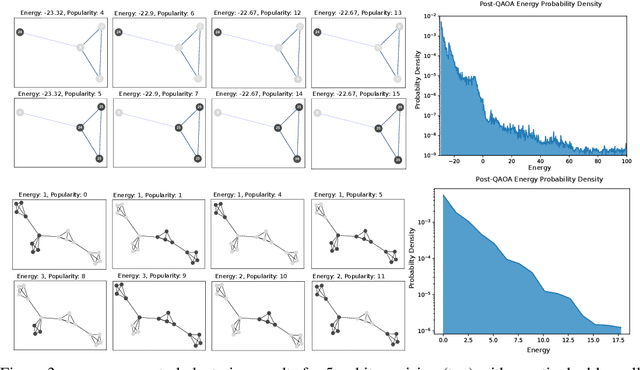
Quantum Neural Networks (QNNs) are a promising variational learning paradigm with applications to near-term quantum processors, however they still face some significant challenges. One such challenge is finding good parameter initialization heuristics that ensure rapid and consistent convergence to local minima of the parameterized quantum circuit landscape. In this work, we train classical neural networks to assist in the quantum learning process, also know as meta-learning, to rapidly find approximate optima in the parameter landscape for several classes of quantum variational algorithms. Specifically, we train classical recurrent neural networks to find approximately optimal parameters within a small number of queries of the cost function for the Quantum Approximate Optimization Algorithm (QAOA) for MaxCut, QAOA for Sherrington-Kirkpatrick Ising model, and for a Variational Quantum Eigensolver for the Hubbard model. By initializing other optimizers at parameter values suggested by the classical neural network, we demonstrate a significant improvement in the total number of optimization iterations required to reach a given accuracy. We further demonstrate that the optimization strategies learned by the neural network generalize well across a range of problem instance sizes. This opens up the possibility of training on small, classically simulatable problem instances, in order to initialize larger, classically intractably simulatable problem instances on quantum devices, thereby significantly reducing the number of required quantum-classical optimization iterations.