Combinatorial Reasoning: Selecting Reasons in Generative AI Pipelines via Combinatorial Optimization

Recent Large Language Models (LLMs) have demonstrated impressive capabilities at tasks that require human intelligence and are a significant step towards human-like artificial intelligence (AI). Yet the performance of LLMs at reasoning tasks have been subpar and the reasoning capability of LLMs is a matter of significant debate. While it has been shown that the choice of the prompting technique to the LLM can alter its performance on a multitude of tasks, including reasoning, the best performing techniques require human-made prompts with the knowledge of the tasks at hand. We introduce a framework for what we call Combinatorial Reasoning (CR), a fully-automated prompting method, where reasons are sampled from an LLM pipeline and mapped into a Quadratic Unconstrained Binary Optimization (QUBO) problem. The framework investigates whether QUBO solutions can be profitably used to select a useful subset of the reasons to construct a Chain-of-Thought style prompt. We explore the acceleration of CR with specialized solvers. We also investigate the performance of simpler zero-shot strategies such as linear majority rule or random selection of reasons. Our preliminary study indicates that coupling a combinatorial solver to generative AI pipelines is an interesting avenue for AI reasoning and elucidates design principles for future CR methods.

Training Deep Boltzmann Networks with Sparse Ising Machines

The slowing down of Moore's law has driven the development of unconventional computing paradigms, such as specialized Ising machines tailored to solve combinatorial optimization problems. In this paper, we show a new application domain for probabilistic bit (p-bit) based Ising machines by training deep generative AI models with them. Using sparse, asynchronous, and massively parallel Ising machines we train deep Boltzmann networks in a hybrid probabilistic-classical computing setup. We use the full MNIST dataset without any downsampling or reduction in hardware-aware network topologies implemented in moderately sized Field Programmable Gate Arrays (FPGA). Our machine, which uses only 4,264 nodes (p-bits) and about 30,000 parameters, achieves the same classification accuracy (90%) as an optimized software-based restricted Boltzmann Machine (RBM) with approximately 3.25 million parameters. Additionally, the sparse deep Boltzmann network can generate new handwritten digits, a task the 3.25 million parameter RBM fails at despite achieving the same accuracy. Our hybrid computer takes a measured 50 to 64 billion probabilistic flips per second, which is at least an order of magnitude faster than superficially similar Graphics and Tensor Processing Unit (GPU/TPU) based implementations. The massively parallel architecture can comfortably perform the contrastive divergence algorithm (CD-n) with up to n = 10 million sweeps per update, beyond the capabilities of existing software implementations. These results demonstrate the potential of using Ising machines for traditionally hard-to-train deep generative Boltzmann networks, with further possible improvement in nanodevice-based realizations.

Quantum advantage in learning from experiments

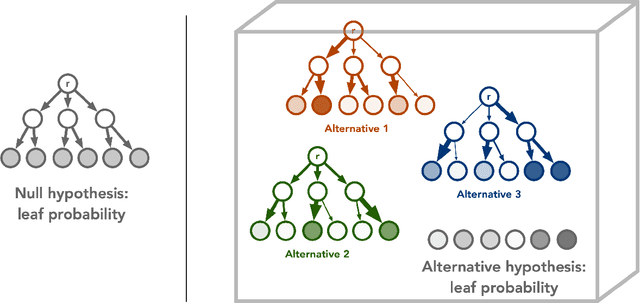
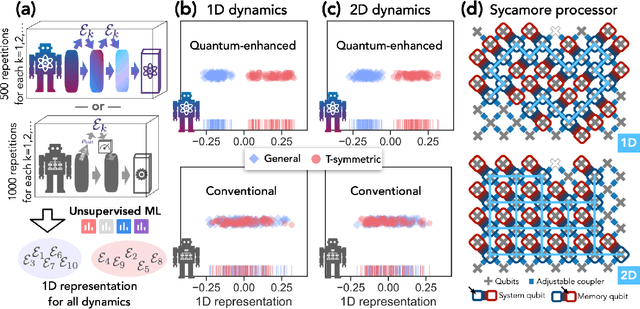
Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.

Nonequilibrium Monte Carlo for unfreezing variables in hard combinatorial optimization

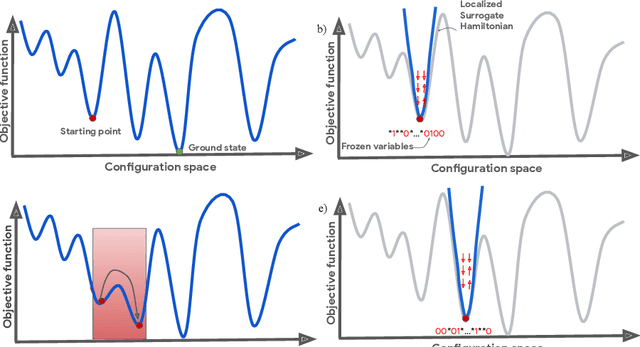
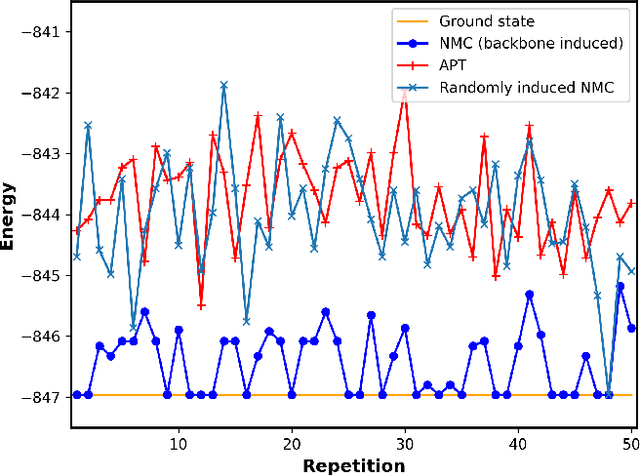
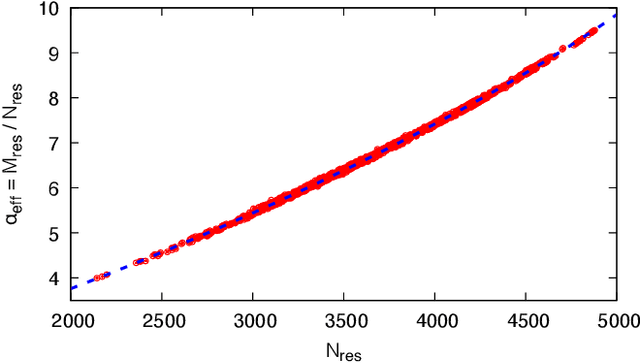
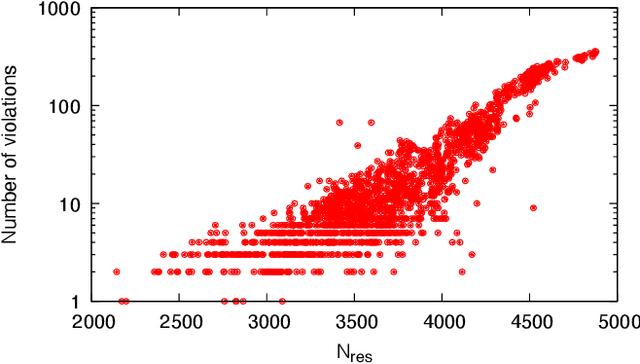
Optimizing highly complex cost/energy functions over discrete variables is at the heart of many open problems across different scientific disciplines and industries. A major obstacle is the emergence of many-body effects among certain subsets of variables in hard instances leading to critical slowing down or collective freezing for known stochastic local search strategies. An exponential computational effort is generally required to unfreeze such variables and explore other unseen regions of the configuration space. Here, we introduce a quantum-inspired family of nonlocal Nonequilibrium Monte Carlo (NMC) algorithms by developing an adaptive gradient-free strategy that can efficiently learn key instance-wise geometrical features of the cost function. That information is employed on-the-fly to construct spatially inhomogeneous thermal fluctuations for collectively unfreezing variables at various length scales, circumventing costly exploration versus exploitation trade-offs. We apply our algorithm to two of the most challenging combinatorial optimization problems: random k-satisfiability (k-SAT) near the computational phase transitions and Quadratic Assignment Problems (QAP). We observe significant speedup and robustness over both specialized deterministic solvers and generic stochastic solvers. In particular, for 90% of random 4-SAT instances we find solutions that are inaccessible for the best specialized deterministic algorithm known as Survey Propagation (SP) with an order of magnitude improvement in the quality of solutions for the hardest 10% instances. We also demonstrate two orders of magnitude improvement in time-to-solution over the state-of-the-art generic stochastic solver known as Adaptive Parallel Tempering (APT).

Power of data in quantum machine learning

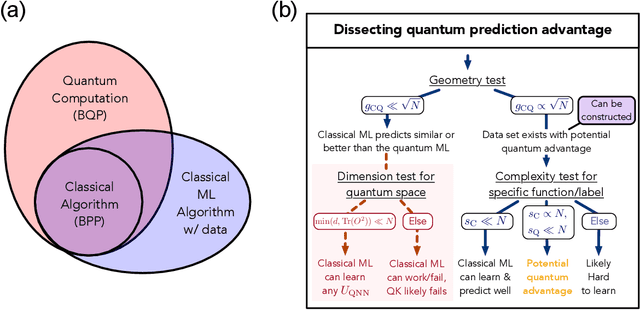
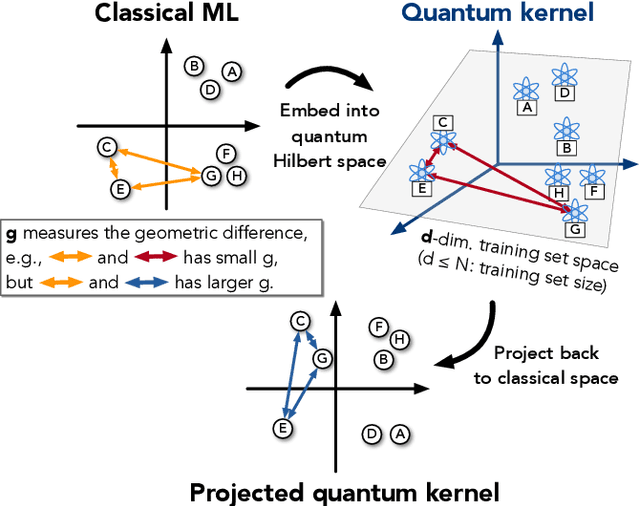
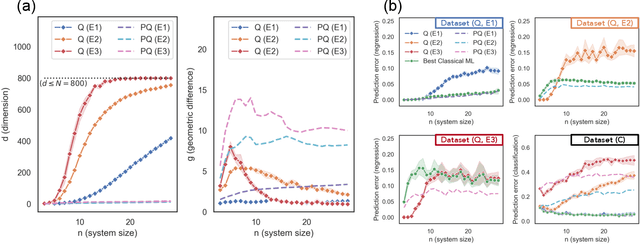
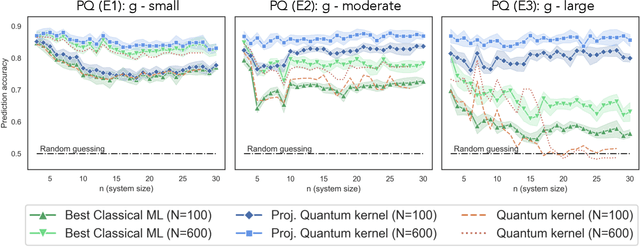
The use of quantum computing for machine learning is among the most exciting prospective applications of quantum technologies. At the crux of excitement is the potential for quantum computers to perform some computations exponentially faster than their classical counterparts. However, a machine learning task where some data is provided can be considerably different than more commonly studied computational tasks. In this work, we show that some problems that are classically hard to compute can be predicted easily with classical machines that learn from data. We find that classical machines can often compete or outperform existing quantum models even on data sets generated by quantum evolution, especially at large system sizes. Using rigorous prediction error bounds as a foundation, we develop a methodology for assessing the potential for quantum advantage in prediction on learning tasks. We show how the use of exponentially large quantum Hilbert space in existing quantum models can result in significantly inferior prediction performance compared to classical machines. To circumvent the observed setbacks, we propose an improvement by projecting all quantum states to an approximate classical representation. The projected quantum model provides a simple and rigorous quantum speed-up for a recently proposed learning problem in the fault-tolerant regime. For more near-term quantum models, the projected versions demonstrate a significant prediction advantage over some classical models on engineered data sets in one of the largest numerical tests for gate-based quantum machine learning to date, up to 30 qubits.

Layerwise learning for quantum neural networks

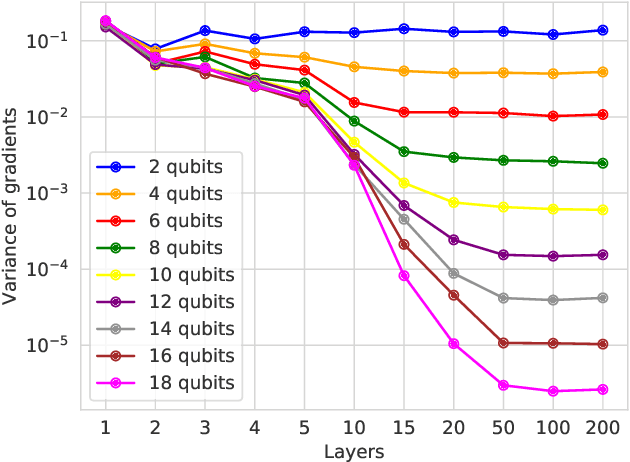
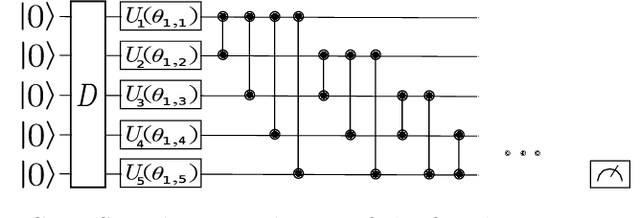
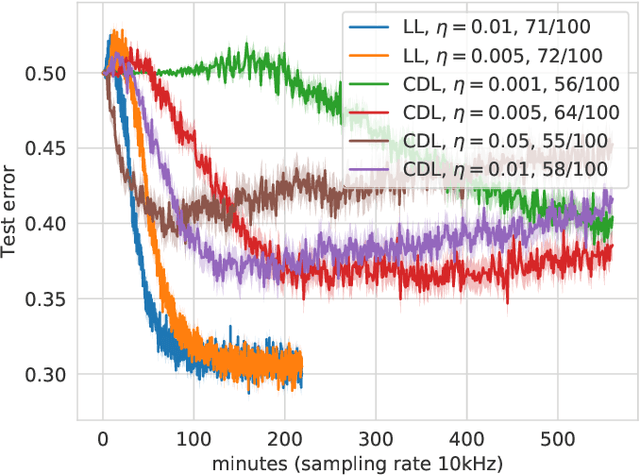
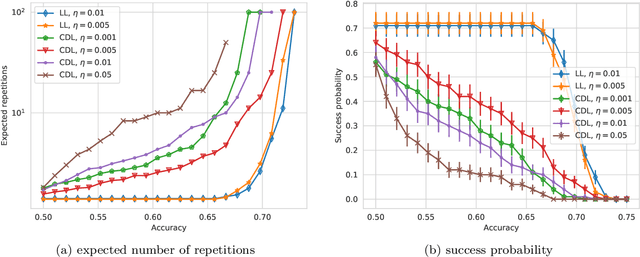
With the increased focus on quantum circuit learning for near-term applications on quantum devices, in conjunction with unique challenges presented by cost function landscapes of parametrized quantum circuits, strategies for effective training are becoming increasingly important. In order to ameliorate some of these challenges, we investigate a layerwise learning strategy for parametrized quantum circuits. The circuit depth is incrementally grown during optimization, and only subsets of parameters are updated in each training step. We show that when considering sampling noise, this strategy can help avoid the problem of barren plateaus of the error surface due to the low depth of circuits, low number of parameters trained in one step, and larger magnitude of gradients compared to training the full circuit. These properties make our algorithm preferable for execution on noisy intermediate-scale quantum devices. We demonstrate our approach on an image-classification task on handwritten digits, and show that layerwise learning attains an 8% lower generalization error on average in comparison to standard learning schemes for training quantum circuits of the same size. Additionally, the percentage of runs that reach lower test errors is up to 40% larger compared to training the full circuit, which is susceptible to creeping onto a plateau during training.

TensorFlow Quantum: A Software Framework for Quantum Machine Learning

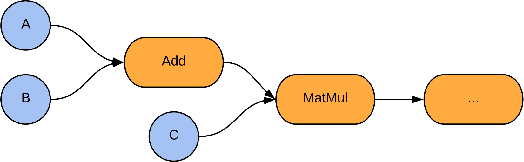
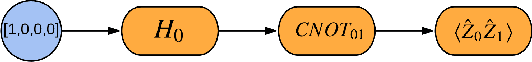
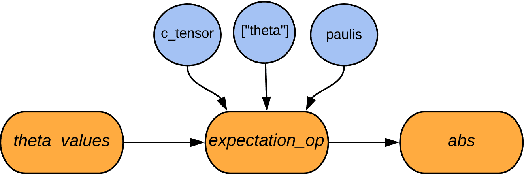
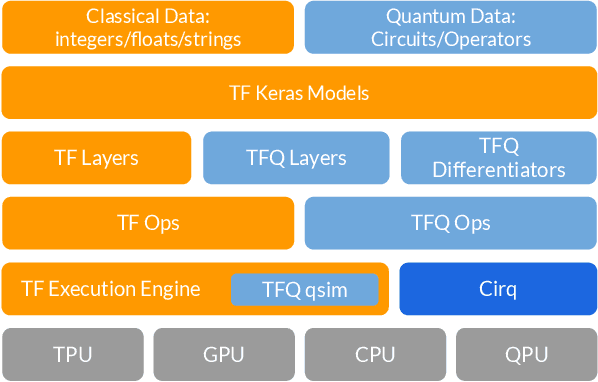
We introduce TensorFlow Quantum (TFQ), an open source library for the rapid prototyping of hybrid quantum-classical models for classical or quantum data. This framework offers high-level abstractions for the design and training of both discriminative and generative quantum models under TensorFlow and supports high-performance quantum circuit simulators. We provide an overview of the software architecture and building blocks through several examples and review the theory of hybrid quantum-classical neural networks. We illustrate TFQ functionalities via several basic applications including supervised learning for quantum classification, quantum control, and quantum approximate optimization. Moreover, we demonstrate how one can apply TFQ to tackle advanced quantum learning tasks including meta-learning, Hamiltonian learning, and sampling thermal states. We hope this framework provides the necessary tools for the quantum computing and machine learning research communities to explore models of both natural and artificial quantum systems, and ultimately discover new quantum algorithms which could potentially yield a quantum advantage.

A Probability Density Theory for Spin-Glass Systems

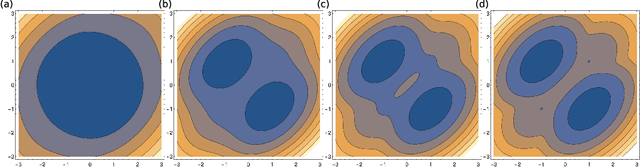
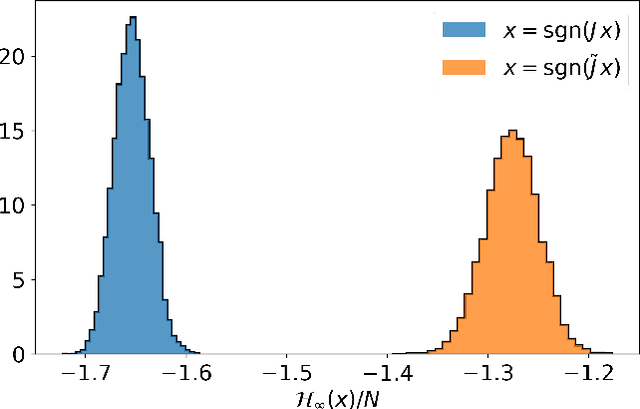
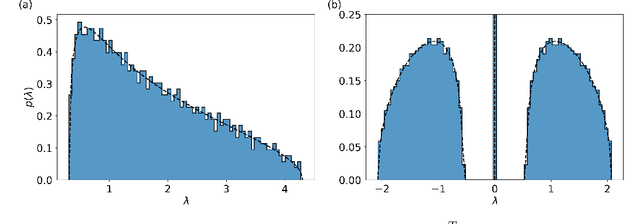
Spin-glass systems are universal models for representing many-body phenomena in statistical physics and computer science. High quality solutions of NP-hard combinatorial optimization problems can be encoded into low energy states of spin-glass systems. In general, evaluating the relevant physical and computational properties of such models is difficult due to critical slowing down near a phase transition. Ideally, one could use recent advances in deep learning for characterizing the low-energy properties of these complex systems. Unfortunately, many of the most promising machine learning approaches are only valid for distributions over continuous variables and thus cannot be directly applied to discrete spin-glass models. To this end, we develop a continuous probability density theory for spin-glass systems with arbitrary dimensions, interactions, and local fields. We show how our formulation geometrically encodes key physical and computational properties of the spin-glass in an instance-wise fashion without the need for quenched disorder averaging. We show that our approach is beyond the mean-field theory and identify a transition from a convex to non-convex energy landscape as the temperature is lowered past a critical temperature. We apply our formalism to a number of spin-glass models including the Sherrington-Kirkpatrick (SK) model, spins on random Erd\H{o}s-R\'enyi graphs, and random restricted Boltzmann machines.

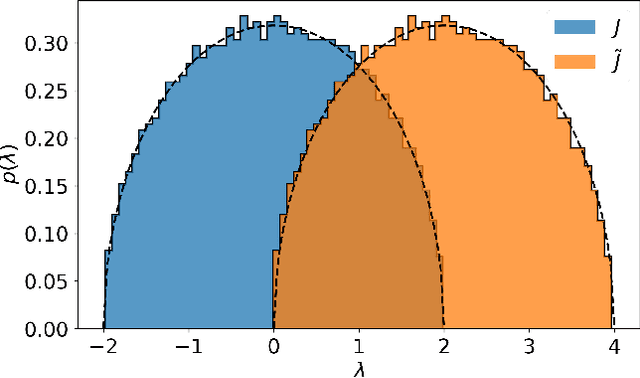
Self-Supervised Learning of Generative Spin-Glasses with Normalizing Flows

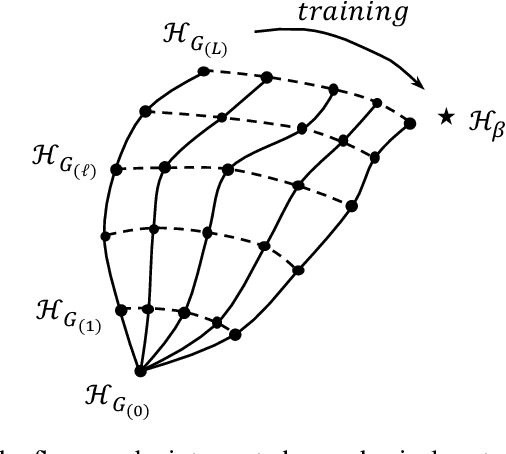
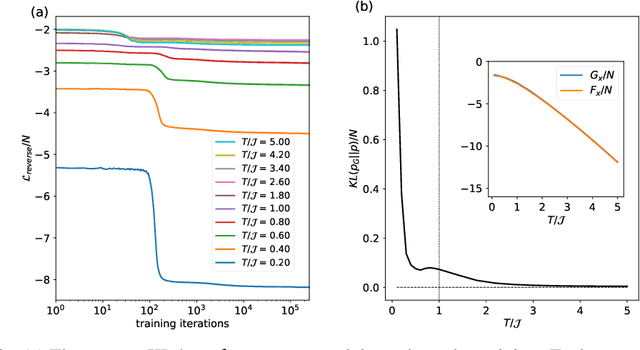
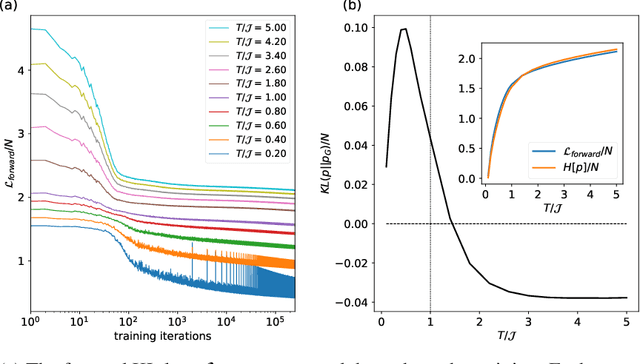
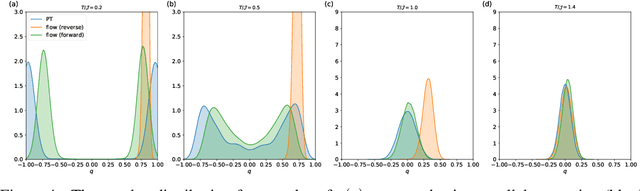
Spin-glasses are universal models that can capture complex behavior of many-body systems at the interface of statistical physics and computer science including discrete optimization, inference in graphical models, and automated reasoning. Computing the underlying structure and dynamics of such complex systems is extremely difficult due to the combinatorial explosion of their state space. Here, we develop deep generative continuous spin-glass distributions with normalizing flows to model correlations in generic discrete problems. We use a self-supervised learning paradigm by automatically generating the data from the spin-glass itself. We demonstrate that key physical and computational properties of the spin-glass phase can be successfully learned, including multi-modal steady-state distributions and topological structures among metastable states. Remarkably, we observe that the learning itself corresponds to a spin-glass phase transition within the layers of the trained normalizing flows. The inverse normalizing flows learns to perform reversible multi-scale coarse-graining operations which are very different from the typical irreversible renormalization group techniques.

Learning to learn with quantum neural networks via classical neural networks

Quantum Neural Networks (QNNs) are a promising variational learning paradigm with applications to near-term quantum processors, however they still face some significant challenges. One such challenge is finding good parameter initialization heuristics that ensure rapid and consistent convergence to local minima of the parameterized quantum circuit landscape. In this work, we train classical neural networks to assist in the quantum learning process, also know as meta-learning, to rapidly find approximate optima in the parameter landscape for several classes of quantum variational algorithms. Specifically, we train classical recurrent neural networks to find approximately optimal parameters within a small number of queries of the cost function for the Quantum Approximate Optimization Algorithm (QAOA) for MaxCut, QAOA for Sherrington-Kirkpatrick Ising model, and for a Variational Quantum Eigensolver for the Hubbard model. By initializing other optimizers at parameter values suggested by the classical neural network, we demonstrate a significant improvement in the total number of optimization iterations required to reach a given accuracy. We further demonstrate that the optimization strategies learned by the neural network generalize well across a range of problem instance sizes. This opens up the possibility of training on small, classically simulatable problem instances, in order to initialize larger, classically intractably simulatable problem instances on quantum devices, thereby significantly reducing the number of required quantum-classical optimization iterations.