Finite Sample Identification of Partially Observed Bilinear Dynamical Systems

We consider the problem of learning a realization of a partially observed bilinear dynamical system (BLDS) from noisy input-output data. Given a single trajectory of input-output samples, we provide a finite time analysis for learning the system's Markov-like parameters, from which a balanced realization of the bilinear system can be obtained. Our bilinear system identification algorithm learns the system's Markov-like parameters by regressing the outputs to highly correlated, nonlinear, and heavy-tailed covariates. Moreover, the stability of BLDS depends on the sequence of inputs used to excite the system. These properties, unique to partially observed bilinear dynamical systems, pose significant challenges to the analysis of our algorithm for learning the unknown dynamics. We address these challenges and provide high probability error bounds on our identification algorithm under a uniform stability assumption. Our analysis provides insights into system theoretic quantities that affect learning accuracy and sample complexity. Lastly, we perform numerical experiments with synthetic data to reinforce these insights.

Learning Linear Dynamics from Bilinear Observations

We consider the problem of learning a realization of a partially observed dynamical system with linear state transitions and bilinear observations. Under very mild assumptions on the process and measurement noises, we provide a finite time analysis for learning the unknown dynamics matrices (up to a similarity transform). Our analysis involves a regression problem with heavy-tailed and dependent data. Moreover, each row of our design matrix contains a Kronecker product of current input with a history of inputs, making it difficult to guarantee persistence of excitation. We overcome these challenges, first providing a data-dependent high probability error bound for arbitrary but fixed inputs. Then, we derive a data-independent error bound for inputs chosen according to a simple random design. Our main results provide an upper bound on the statistical error rates and sample complexity of learning the unknown dynamics matrices from a single finite trajectory of bilinear observations.

Random Features Approximation for Control-Affine Systems

Modern data-driven control applications call for flexible nonlinear models that are amenable to principled controller synthesis and realtime feedback. Many nonlinear dynamical systems of interest are control affine. We propose two novel classes of nonlinear feature representations which capture control affine structure while allowing for arbitrary complexity in the state dependence. Our methods make use of random features (RF) approximations, inheriting the expressiveness of kernel methods at a lower computational cost. We formalize the representational capabilities of our methods by showing their relationship to the Affine Dot Product (ADP) kernel proposed by Casta\~neda et al. (2021) and a novel Affine Dense (AD) kernel that we introduce. We further illustrate the utility by presenting a case study of data-driven optimization-based control using control certificate functions (CCF). Simulation experiments on a double pendulum empirically demonstrate the advantages of our methods.

Finite Sample Identification of Bilinear Dynamical Systems

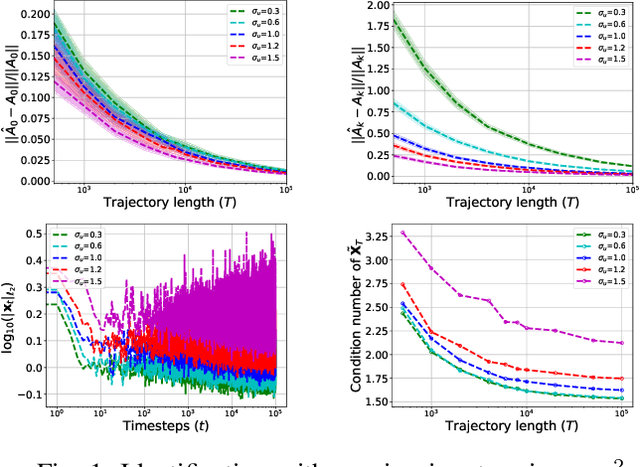
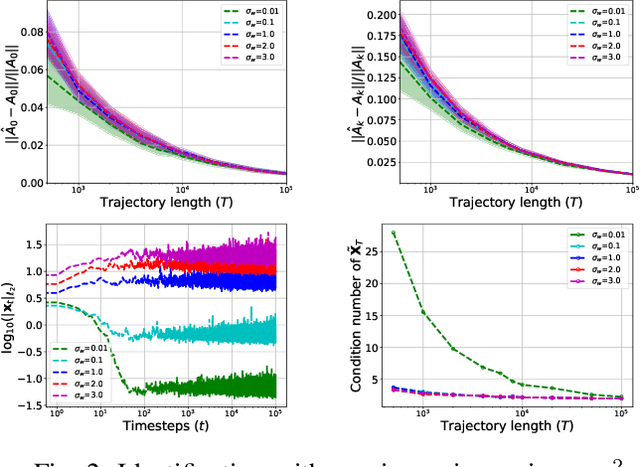
Bilinear dynamical systems are ubiquitous in many different domains and they can also be used to approximate more general control-affine systems. This motivates the problem of learning bilinear systems from a single trajectory of the system's states and inputs. Under a mild marginal mean-square stability assumption, we identify how much data is needed to estimate the unknown bilinear system up to a desired accuracy with high probability. Our sample complexity and statistical error rates are optimal in terms of the trajectory length, the dimensionality of the system and the input size. Our proof technique relies on an application of martingale small-ball condition. This enables us to correctly capture the properties of the problem, specifically our error rates do not deteriorate with increasing instability. Finally, we show that numerical experiments are well-aligned with our theoretical results.

Identification and Adaptive Control of Markov Jump Systems: Sample Complexity and Regret Bounds

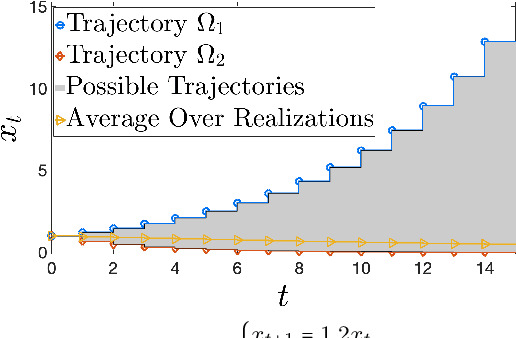
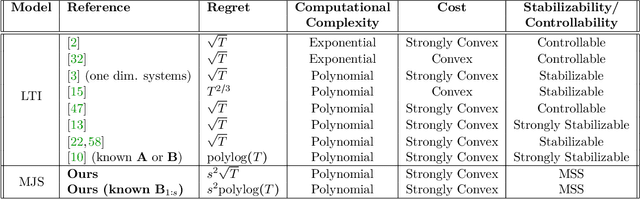
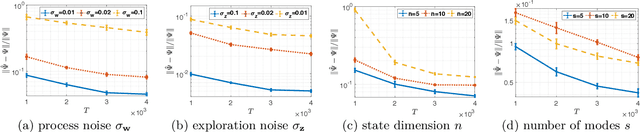
Learning how to effectively control unknown dynamical systems is crucial for intelligent autonomous systems. This task becomes a significant challenge when the underlying dynamics are changing with time. Motivated by this challenge, this paper considers the problem of controlling an unknown Markov jump linear system (MJS) to optimize a quadratic objective. By taking a model-based perspective, we consider identification-based adaptive control for MJSs. We first provide a system identification algorithm for MJS to learn the dynamics in each mode as well as the Markov transition matrix, underlying the evolution of the mode switches, from a single trajectory of the system states, inputs, and modes. Through mixing-time arguments, sample complexity of this algorithm is shown to be $\mathcal{O}(1/\sqrt{T})$. We then propose an adaptive control scheme that performs system identification together with certainty equivalent control to adapt the controllers in an episodic fashion. Combining our sample complexity results with recent perturbation results for certainty equivalent control, we prove that when the episode lengths are appropriately chosen, the proposed adaptive control scheme achieves $\mathcal{O}(\sqrt{T})$ regret, which can be improved to $\mathcal{O}(polylog(T))$ with partial knowledge of the system. Our proof strategy introduces innovations to handle Markovian jumps and a weaker notion of stability common in MJSs. Our analysis provides insights into system theoretic quantities that affect learning accuracy and control performance. Numerical simulations are presented to further reinforce these insights.

Certainty Equivalent Quadratic Control for Markov Jump Systems

Real-world control applications often involve complex dynamics subject to abrupt changes or variations. Markov jump linear systems (MJS) provide a rich framework for modeling such dynamics. Despite an extensive history, theoretical understanding of parameter sensitivities of MJS control is somewhat lacking. Motivated by this, we investigate robustness aspects of certainty equivalent model-based optimal control for MJS with quadratic cost function. Given the uncertainty in the system matrices and in the Markov transition matrix is bounded by $\epsilon$ and $\eta$ respectively, robustness results are established for (i) the solution to coupled Riccati equations and (ii) the optimal cost, by providing explicit perturbation bounds which decay as $\mathcal{O}(\epsilon + \eta)$ and $\mathcal{O}((\epsilon + \eta)^2)$ respectively.

Exploring Weight Importance and Hessian Bias in Model Pruning

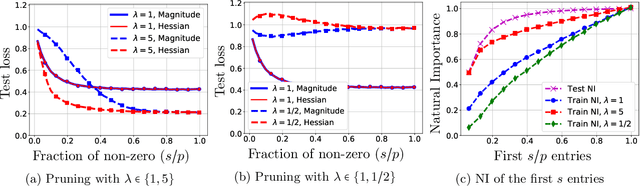
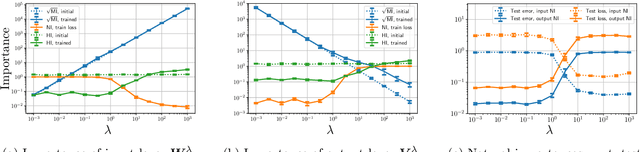
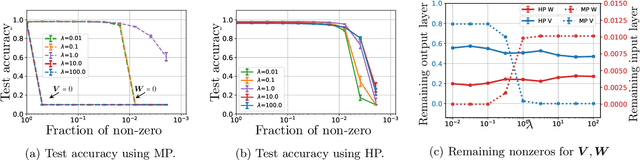
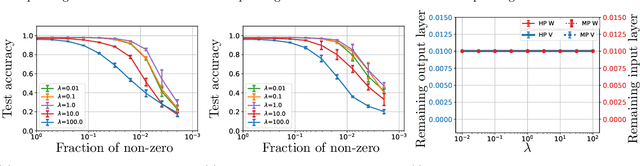
Model pruning is an essential procedure for building compact and computationally-efficient machine learning models. A key feature of a good pruning algorithm is that it accurately quantifies the relative importance of the model weights. While model pruning has a rich history, we still don't have a full grasp of the pruning mechanics even for relatively simple problems involving linear models or shallow neural nets. In this work, we provide a principled exploration of pruning by building on a natural notion of importance. For linear models, we show that this notion of importance is captured by covariance scaling which connects to the well-known Hessian-based pruning. We then derive asymptotic formulas that allow us to precisely compare the performance of different pruning methods. For neural networks, we demonstrate that the importance can be at odds with larger magnitudes and proper initialization is critical for magnitude-based pruning. Specifically, we identify settings in which weights become more important despite becoming smaller, which in turn leads to a catastrophic failure of magnitude-based pruning. Our results also elucidate that implicit regularization in the form of Hessian structure has a catalytic role in identifying the important weights, which dictate the pruning performance.

Non-asymptotic and Accurate Learning of Nonlinear Dynamical Systems

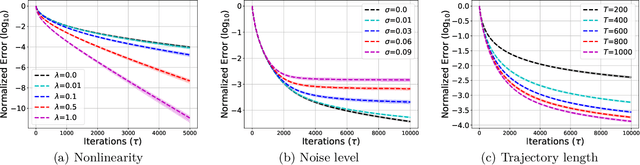
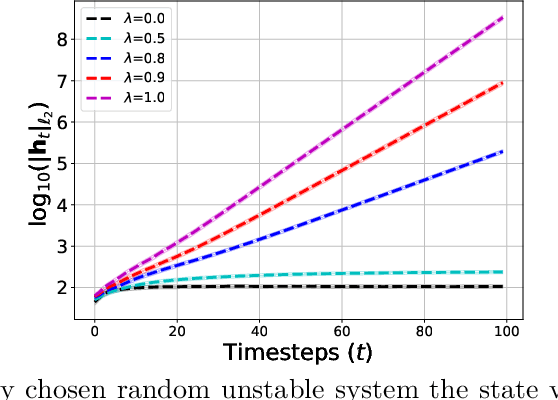
We consider the problem of learning stabilizable systems governed by nonlinear state equation $h_{t+1}=\phi(h_t,u_t;\theta)+w_t$. Here $\theta$ is the unknown system dynamics, $h_t $ is the state, $u_t$ is the input and $w_t$ is the additive noise vector. We study gradient based algorithms to learn the system dynamics $\theta$ from samples obtained from a single finite trajectory. If the system is run by a stabilizing input policy, we show that temporally-dependent samples can be approximated by i.i.d. samples via a truncation argument by using mixing-time arguments. We then develop new guarantees for the uniform convergence of the gradients of empirical loss. Unlike existing work, our bounds are noise sensitive which allows for learning ground-truth dynamics with high accuracy and small sample complexity. Together, our results facilitate efficient learning of the general nonlinear system under stabilizing policy. We specialize our guarantees to entry-wise nonlinear activations and verify our theory in various numerical experiments

Quickly Finding the Best Linear Model in High Dimensions

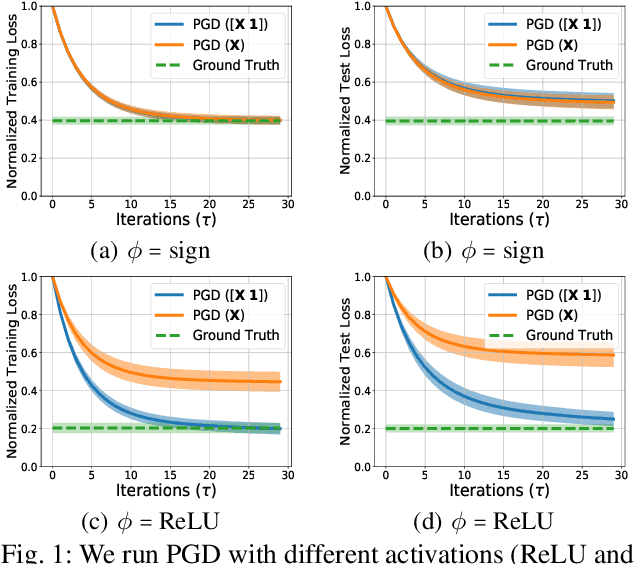
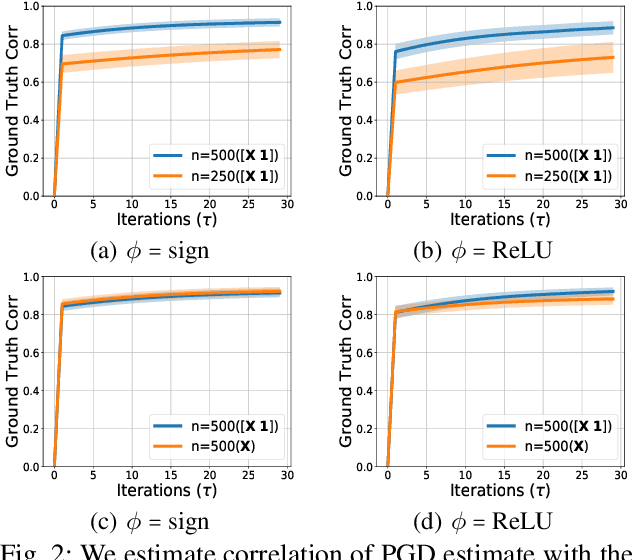
We study the problem of finding the best linear model that can minimize least-squares loss given a data-set. While this problem is trivial in the low dimensional regime, it becomes more interesting in high dimensions where the population minimizer is assumed to lie on a manifold such as sparse vectors. We propose projected gradient descent (PGD) algorithm to estimate the population minimizer in the finite sample regime. We establish linear convergence rate and data dependent estimation error bounds for PGD. Our contributions include: 1) The results are established for heavier tailed sub-exponential distributions besides sub-gaussian. 2) We directly analyze the empirical risk minimization and do not require a realizable model that connects input data and labels. 3) Our PGD algorithm is augmented to learn the bias terms which boosts the performance. The numerical experiments validate our theoretical results.