MatterGen: a generative model for inorganic materials design

The design of functional materials with desired properties is essential in driving technological advances in areas like energy storage, catalysis, and carbon capture. Generative models provide a new paradigm for materials design by directly generating entirely novel materials given desired property constraints. Despite recent progress, current generative models have low success rate in proposing stable crystals, or can only satisfy a very limited set of property constraints. Here, we present MatterGen, a model that generates stable, diverse inorganic materials across the periodic table and can further be fine-tuned to steer the generation towards a broad range of property constraints. To enable this, we introduce a new diffusion-based generative process that produces crystalline structures by gradually refining atom types, coordinates, and the periodic lattice. We further introduce adapter modules to enable fine-tuning towards any given property constraints with a labeled dataset. Compared to prior generative models, structures produced by MatterGen are more than twice as likely to be novel and stable, and more than 15 times closer to the local energy minimum. After fine-tuning, MatterGen successfully generates stable, novel materials with desired chemistry, symmetry, as well as mechanical, electronic and magnetic properties. Finally, we demonstrate multi-property materials design capabilities by proposing structures that have both high magnetic density and a chemical composition with low supply-chain risk. We believe that the quality of generated materials and the breadth of MatterGen's capabilities represent a major advancement towards creating a universal generative model for materials design.

Latent Representation and Simulation of Markov Processes via Time-Lagged Information Bottleneck

Markov processes are widely used mathematical models for describing dynamic systems in various fields. However, accurately simulating large-scale systems at long time scales is computationally expensive due to the short time steps required for accurate integration. In this paper, we introduce an inference process that maps complex systems into a simplified representational space and models large jumps in time. To achieve this, we propose Time-lagged Information Bottleneck (T-IB), a principled objective rooted in information theory, which aims to capture relevant temporal features while discarding high-frequency information to simplify the simulation task and minimize the inference error. Our experiments demonstrate that T-IB learns information-optimal representations for accurately modeling the statistical properties and dynamics of the original process at a selected time lag, outperforming existing time-lagged dimensionality reduction methods.

Timewarp: Transferable Acceleration of Molecular Dynamics by Learning Time-Coarsened Dynamics

Molecular dynamics (MD) simulation is a widely used technique to simulate molecular systems, most commonly at the all-atom resolution where the equations of motion are integrated with timesteps on the order of femtoseconds ($1\textrm{fs}=10^{-15}\textrm{s}$). MD is often used to compute equilibrium properties, which requires sampling from an equilibrium distribution such as the Boltzmann distribution. However, many important processes, such as binding and folding, occur over timescales of milliseconds or beyond, and cannot be efficiently sampled with conventional MD. Furthermore, new MD simulations need to be performed from scratch for each molecular system studied. We present Timewarp, an enhanced sampling method which uses a normalising flow as a proposal distribution in a Markov chain Monte Carlo method targeting the Boltzmann distribution. The flow is trained offline on MD trajectories and learns to make large steps in time, simulating the molecular dynamics of $10^{5} - 10^{6}\:\textrm{fs}$. Crucially, Timewarp is transferable between molecular systems: once trained, we show that it generalises to unseen small peptides (2-4 amino acids), exploring their metastable states and providing wall-clock acceleration when sampling compared to standard MD. Our method constitutes an important step towards developing general, transferable algorithms for accelerating MD.

DistIR: An Intermediate Representation and Simulator for Efficient Neural Network Distribution

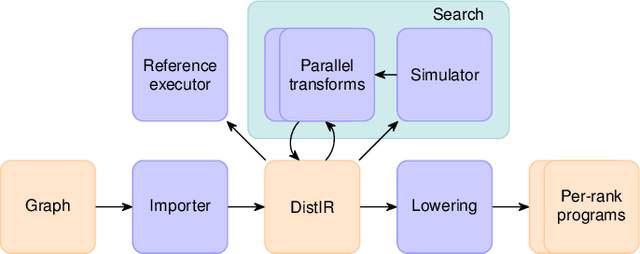
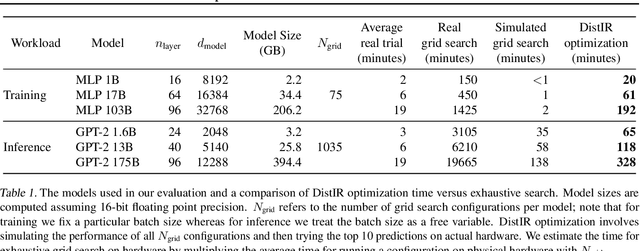
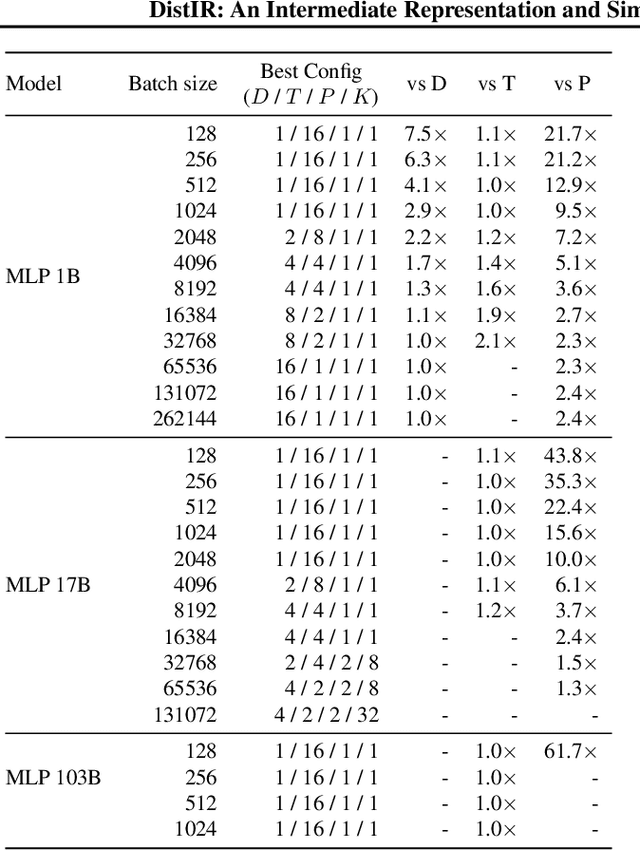
The rapidly growing size of deep neural network (DNN) models and datasets has given rise to a variety of distribution strategies such as data, tensor-model, pipeline parallelism, and hybrid combinations thereof. Each of these strategies offers its own trade-offs and exhibits optimal performance across different models and hardware topologies. Selecting the best set of strategies for a given setup is challenging because the search space grows combinatorially, and debugging and testing on clusters is expensive. In this work we propose DistIR, an expressive intermediate representation for distributed DNN computation that is tailored for efficient analyses, such as simulation. This enables automatically identifying the top-performing strategies without having to execute on physical hardware. Unlike prior work, DistIR can naturally express many distribution strategies including pipeline parallelism with arbitrary schedules. Our evaluation on MLP training and GPT-2 inference models demonstrates how DistIR and its simulator enable fast grid searches over complex distribution spaces spanning up to 1000+ configurations, reducing optimization time by an order of magnitude for certain regimes.

An Information-theoretic Approach to Distribution Shifts

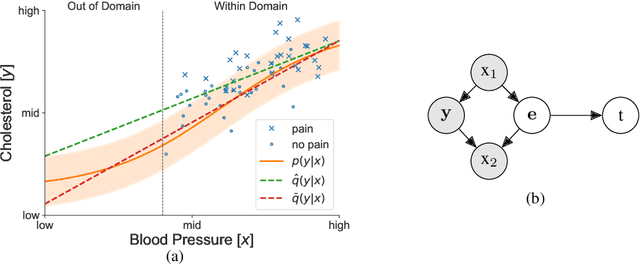
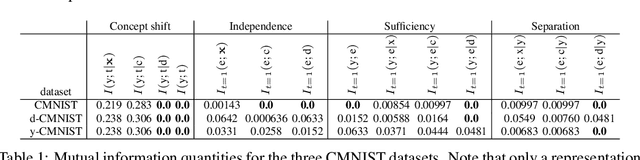
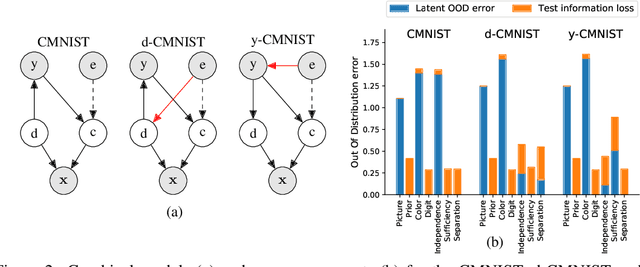
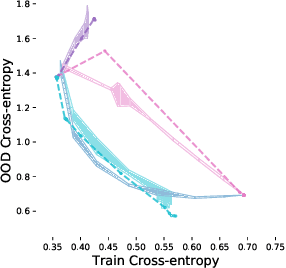
Safely deploying machine learning models to the real world is often a challenging process. Models trained with data obtained from a specific geographic location tend to fail when queried with data obtained elsewhere, agents trained in a simulation can struggle to adapt when deployed in the real world or novel environments, and neural networks that are fit to a subset of the population might carry some selection bias into their decision process. In this work, we describe the problem of data shift from a novel information-theoretic perspective by (i) identifying and describing the different sources of error, (ii) comparing some of the most promising objectives explored in the recent domain generalization, and fair classification literature. From our theoretical analysis and empirical evaluation, we conclude that the model selection procedure needs to be guided by careful considerations regarding the observed data, the factors used for correction, and the structure of the data-generating process.

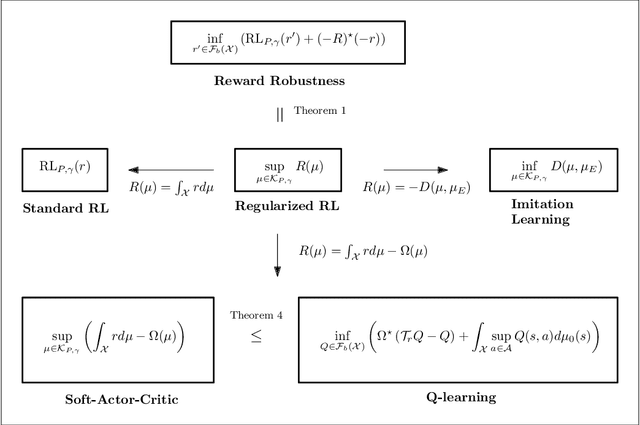
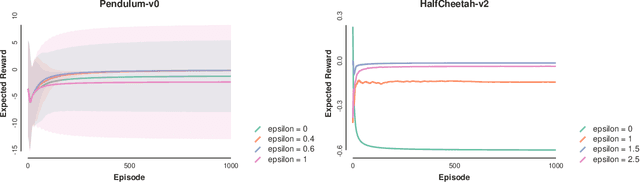
Regularized Policies are Reward Robust

Entropic regularization of policies in Reinforcement Learning (RL) is a commonly used heuristic to ensure that the learned policy explores the state-space sufficiently before overfitting to a local optimal policy. The primary motivation for using entropy is for exploration and disambiguating optimal policies; however, the theoretical effects are not entirely understood. In this work, we study the more general regularized RL objective and using Fenchel duality; we derive the dual problem which takes the form of an adversarial reward problem. In particular, we find that the optimal policy found by a regularized objective is precisely an optimal policy of a reinforcement learning problem under a worst-case adversarial reward. Our result allows us to reinterpret the popular entropic regularization scheme as a form of robustification. Furthermore, due to the generality of our results, we apply to other existing regularization schemes. Our results thus give insights into the effects of regularization of policies and deepen our understanding of exploration through robust rewards at large.

On the Loss Landscape of Adversarial Training: Identifying Challenges and How to Overcome Them

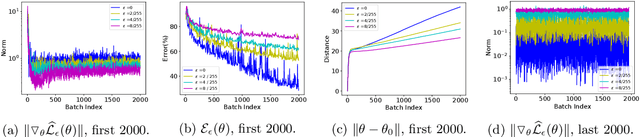
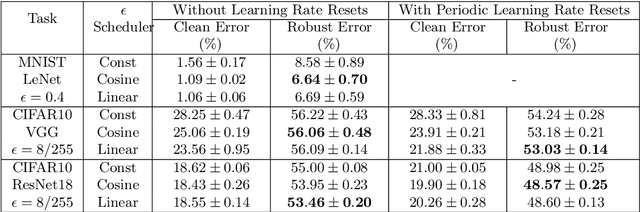
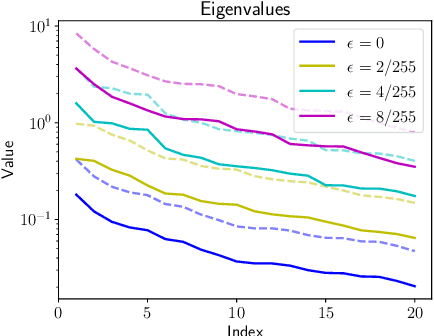
We analyze the influence of adversarial training on the loss landscape of machine learning models. To this end, we first provide analytical studies of the properties of adversarial loss functions under different adversarial budgets. We then demonstrate that the adversarial loss landscape is less favorable to optimization, due to increased curvature and more scattered gradients. Our conclusions are validated by numerical analyses, which show that training under large adversarial budgets impede the escape from suboptimal random initialization, cause non-vanishing gradients and make the model find sharper minima. Based on these observations, we show that a periodic adversarial scheduling (PAS) strategy can effectively overcome these challenges, yielding better results than vanilla adversarial training while being much less sensitive to the choice of learning rate.

On Certifying Non-uniform Bound against Adversarial Attacks

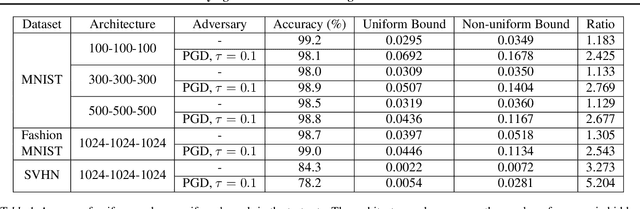
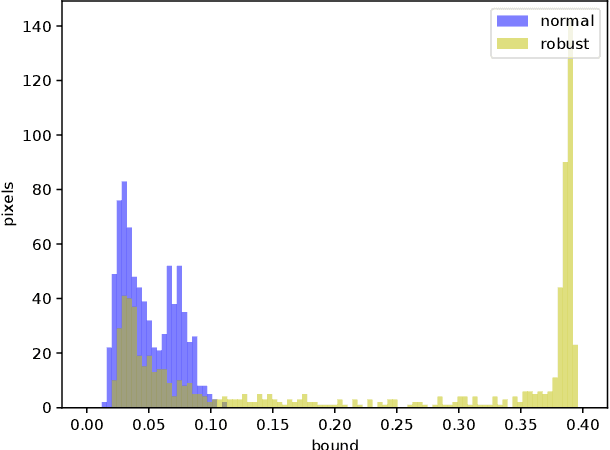
This work studies the robustness certification problem of neural network models, which aims to find certified adversary-free regions as large as possible around data points. In contrast to the existing approaches that seek regions bounded uniformly along all input features, we consider non-uniform bounds and use it to study the decision boundary of neural network models. We formulate our target as an optimization problem with nonlinear constraints. Then, a framework applicable for general feedforward neural networks is proposed to bound the output logits so that the relaxed problem can be solved by the augmented Lagrangian method. Our experiments show the non-uniform bounds have larger volumes than uniform ones. Compared with normal models, the robust models have even larger non-uniform bounds and better interpretability. Further, the geometric similarity of the non-uniform bounds gives a quantitative, data-agnostic metric of input features' robustness.

Hierarchical Representations with Poincaré Variational Auto-Encoders

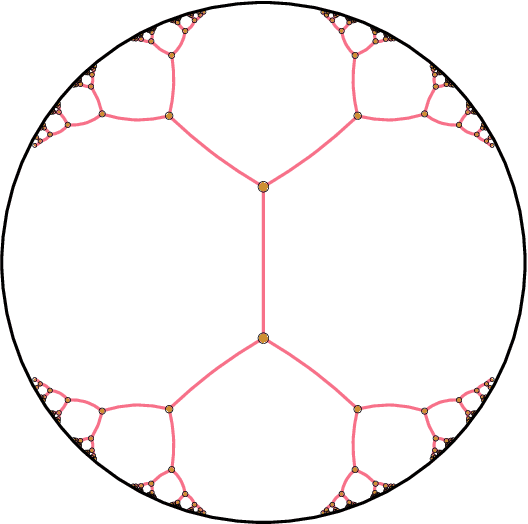
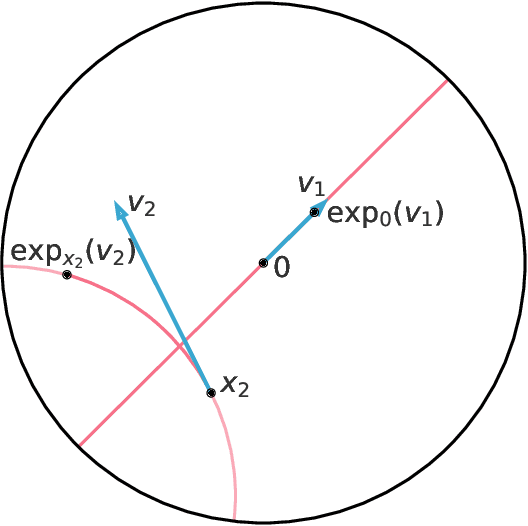
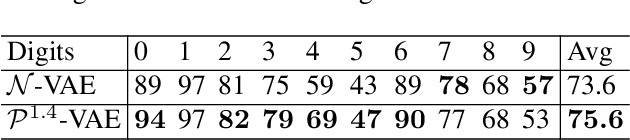
The Variational Auto-Encoder (VAE) model has become widely popular as a way to learn at once a generative model and embeddings for observations living in a high-dimensional space. In the real world, many such observations may be assumed to be hierarchically structured, such as living organisms data which are related through the evolutionary tree. Also, it has been theoretically and empirically shown that data with hierarchical structure can efficiently be embedded in hyperbolic spaces. We therefore endow the VAE with a hyperbolic geometry and empirically show that it can better generalise to unseen data than its Euclidean counterpart, and can qualitatively recover the hierarchical structure.

Depth and nonlinearity induce implicit exploration for RL

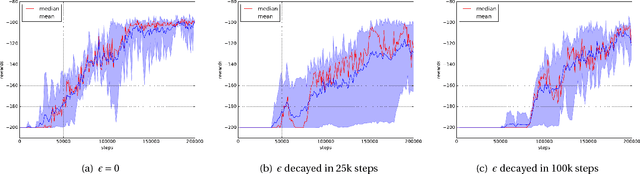
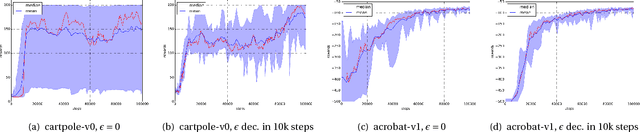
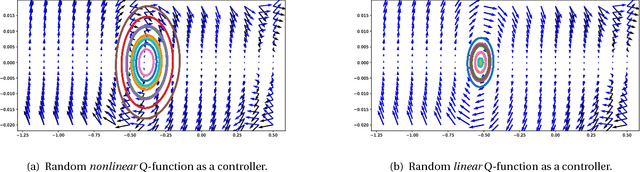
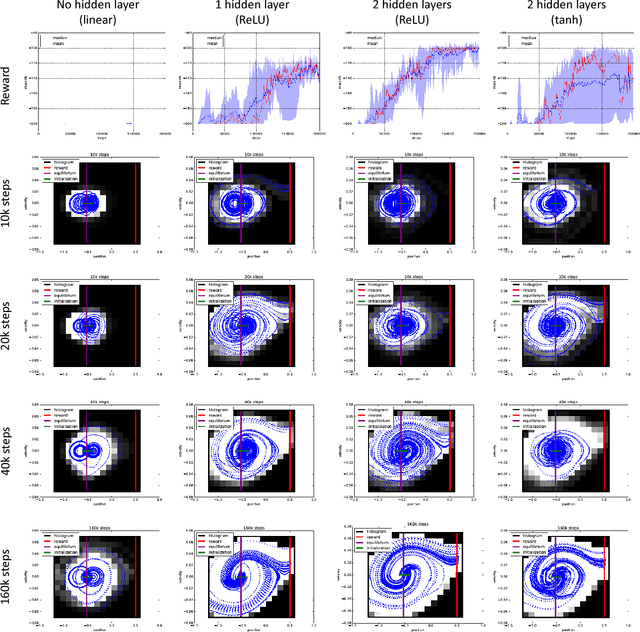
The question of how to explore, i.e., take actions with uncertain outcomes to learn about possible future rewards, is a key question in reinforcement learning (RL). Here, we show a surprising result: We show that Q-learning with nonlinear Q-function and no explicit exploration (i.e., a purely greedy policy) can learn several standard benchmark tasks, including mountain car, equally well as, or better than, the most commonly-used $\epsilon$-greedy exploration. We carefully examine this result and show that both the depth of the Q-network and the type of nonlinearity are important to induce such deterministic exploration.