Geometric Collaborative Filtering with Convergence

Latent variable collaborative filtering methods have been a standard approach to modelling user-click interactions due to their simplicity and effectiveness. However, there is limited work on analyzing the mathematical properties of these methods in particular on preventing the overfitting towards the identity, and such methods typically utilize loss functions that overlook the geometry between items. In this work, we introduce a notion of generalization gap in collaborative filtering and analyze this with respect to latent collaborative filtering models. We present a geometric upper bound that gives rise to loss functions, and a way to meaningfully utilize the geometry of item-metadata to improve recommendations. We show how these losses can be minimized and gives the recipe to a new latent collaborative filtering algorithm, which we refer to as GeoCF, due to the geometric nature of our results. We then show experimentally that our proposed GeoCF algorithm can outperform other all existing methods on the Movielens20M and Netflix datasets, as well as two large-scale internal datasets. In summary, our work proposes a theoretically sound method which paves a way to better understand generalization of collaborative filtering at large.

Self-Supervision Improves Diffusion Models for Tabular Data Imputation

The ubiquity of missing data has sparked considerable attention and focus on tabular data imputation methods. Diffusion models, recognized as the cutting-edge technique for data generation, demonstrate significant potential in tabular data imputation tasks. However, in pursuit of diversity, vanilla diffusion models often exhibit sensitivity to initialized noises, which hinders the models from generating stable and accurate imputation results. Additionally, the sparsity inherent in tabular data poses challenges for diffusion models in accurately modeling the data manifold, impacting the robustness of these models for data imputation. To tackle these challenges, this paper introduces an advanced diffusion model named Self-supervised imputation Diffusion Model (SimpDM for brevity), specifically tailored for tabular data imputation tasks. To mitigate sensitivity to noise, we introduce a self-supervised alignment mechanism that aims to regularize the model, ensuring consistent and stable imputation predictions. Furthermore, we introduce a carefully devised state-dependent data augmentation strategy within SimpDM, enhancing the robustness of the diffusion model when dealing with limited data. Extensive experiments demonstrate that SimpDM matches or outperforms state-of-the-art imputation methods across various scenarios.

Rejection via Learning Density Ratios

Classification with rejection emerges as a learning paradigm which allows models to abstain from making predictions. The predominant approach is to alter the supervised learning pipeline by augmenting typical loss functions, letting model rejection incur a lower loss than an incorrect prediction. Instead, we propose a different distributional perspective, where we seek to find an idealized data distribution which maximizes a pretrained model's performance. This can be formalized via the optimization of a loss's risk with a $ \phi$-divergence regularization term. Through this idealized distribution, a rejection decision can be made by utilizing the density ratio between this distribution and the data distribution. We focus on the setting where our $ \phi $-divergences are specified by the family of $ \alpha $-divergence. Our framework is tested empirically over clean and noisy datasets.

Distributionally Robust Bayesian Optimization with $φ$-divergences

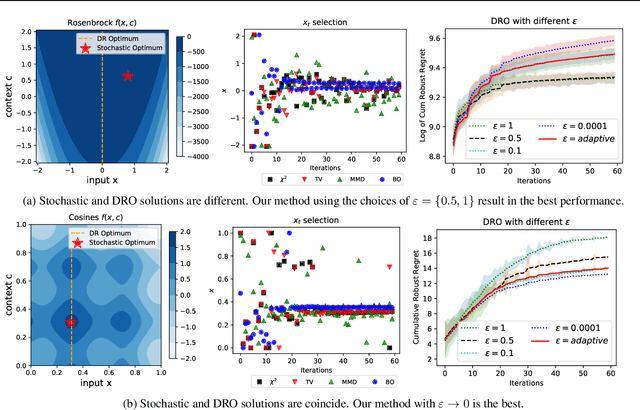
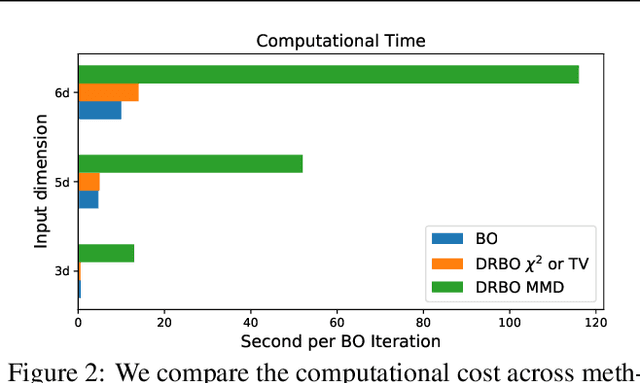
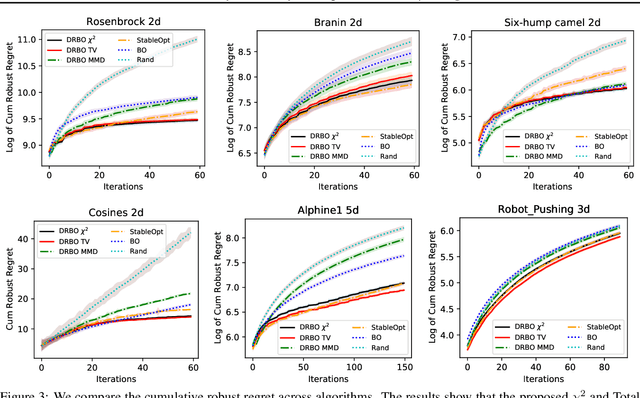
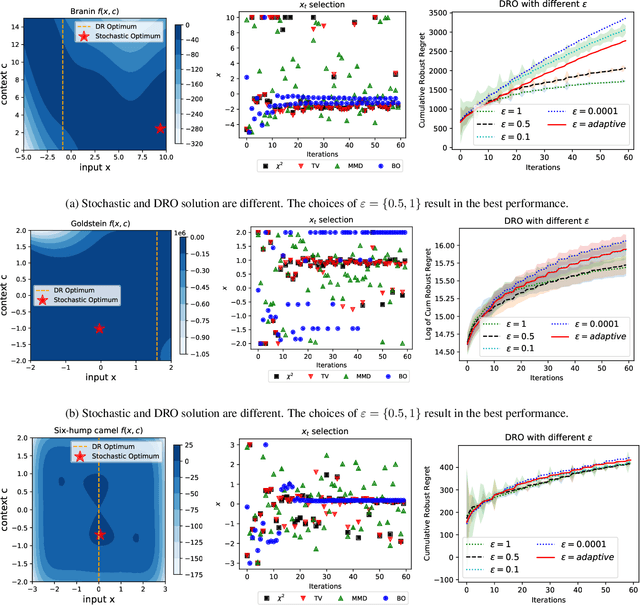
The study of robustness has received much attention due to its inevitability in data-driven settings where many systems face uncertainty. One such example of concern is Bayesian Optimization (BO), where uncertainty is multi-faceted, yet there only exists a limited number of works dedicated to this direction. In particular, there is the work of Kirschner et al. (2020), which bridges the existing literature of Distributionally Robust Optimization (DRO) by casting the BO problem from the lens of DRO. While this work is pioneering, it admittedly suffers from various practical shortcomings such as finite contexts assumptions, leaving behind the main question Can one devise a computationally tractable algorithm for solving this DRO-BO problem? In this work, we tackle this question to a large degree of generality by considering robustness against data-shift in $\phi$-divergences, which subsumes many popular choices, such as the $\chi^2$-divergence, Total Variation, and the extant Kullback-Leibler (KL) divergence. We show that the DRO-BO problem in this setting is equivalent to a finite-dimensional optimization problem which, even in the continuous context setting, can be easily implemented with provable sublinear regret bounds. We then show experimentally that our method surpasses existing methods, attesting to the theoretical results

A Law of Robustness for Weight-bounded Neural Networks

Robustness of deep neural networks against adversarial perturbations is a pressing concern motivated by recent findings showing the pervasive nature of such vulnerabilities. One method of characterizing the robustness of a neural network model is through its Lipschitz constant, which forms a robustness certificate. A natural question to ask is, for a fixed model class (such as neural networks) and a dataset of size $n$, what is the smallest achievable Lipschitz constant among all models that fit the dataset? Recently, (Bubeck et al., 2020) conjectured that when using two-layer networks with $k$ neurons to fit a generic dataset, the smallest Lipschitz constant is $\Omega(\sqrt{\frac{n}{k}})$. This implies that one would require one neuron per data point to robustly fit the data. In this work we derive a lower bound on the Lipschitz constant for any arbitrary model class with bounded Rademacher complexity. Our result coincides with that conjectured in (Bubeck et al., 2020) for two-layer networks under the assumption of bounded weights. However, due to our result's generality, we also derive bounds for multi-layer neural networks, discovering that one requires $\log n$ constant-sized layers to robustly fit the data. Thus, our work establishes a law of robustness for weight bounded neural networks and provides formal evidence on the necessity of over-parametrization in deep learning.

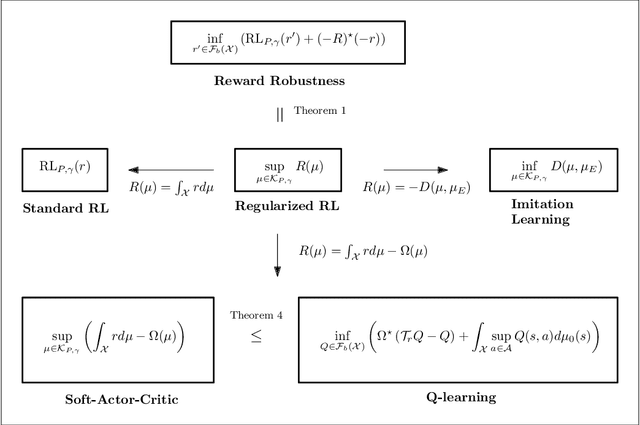
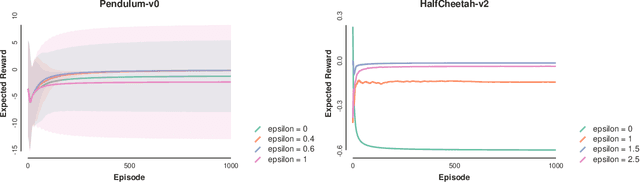
Regularized Policies are Reward Robust

Entropic regularization of policies in Reinforcement Learning (RL) is a commonly used heuristic to ensure that the learned policy explores the state-space sufficiently before overfitting to a local optimal policy. The primary motivation for using entropy is for exploration and disambiguating optimal policies; however, the theoretical effects are not entirely understood. In this work, we study the more general regularized RL objective and using Fenchel duality; we derive the dual problem which takes the form of an adversarial reward problem. In particular, we find that the optimal policy found by a regularized objective is precisely an optimal policy of a reinforcement learning problem under a worst-case adversarial reward. Our result allows us to reinterpret the popular entropic regularization scheme as a form of robustification. Furthermore, due to the generality of our results, we apply to other existing regularization schemes. Our results thus give insights into the effects of regularization of policies and deepen our understanding of exploration through robust rewards at large.

Risk-Monotonicity in Statistical Learning

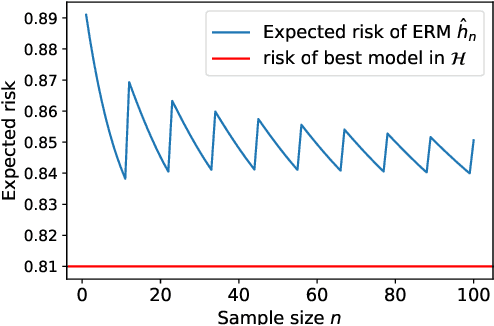
Acquisition of data is a difficult task in many applications of machine learning, and it is only natural that one hopes and expects the populating risk to decrease (better performance) monotonically with increasing data points. It turns out, somewhat surprisingly, that this is not the case even for the most standard algorithms such as empirical risk minimization. Non-monotonic behaviour of the risk and instability in training have manifested and appeared in the popular deep learning paradigm under the description of double descent. These problems highlight bewilderment in our understanding of learning algorithms and generalization. It is, therefore, crucial to pursue this concern and provide a characterization of such behaviour. In this paper, we derive the first consistent and risk-monotonic algorithms for a general statistical learning setting under weak assumptions, consequently resolving an open problem (Viering et al. 2019) on how to avoid non-monotonic behaviour of risk curves. Our work makes a significant contribution to the topic of risk-monotonicity, which may be key in resolving empirical phenomena such as double descent.

Data Preprocessing to Mitigate Bias with Boosted Fair Mollifiers

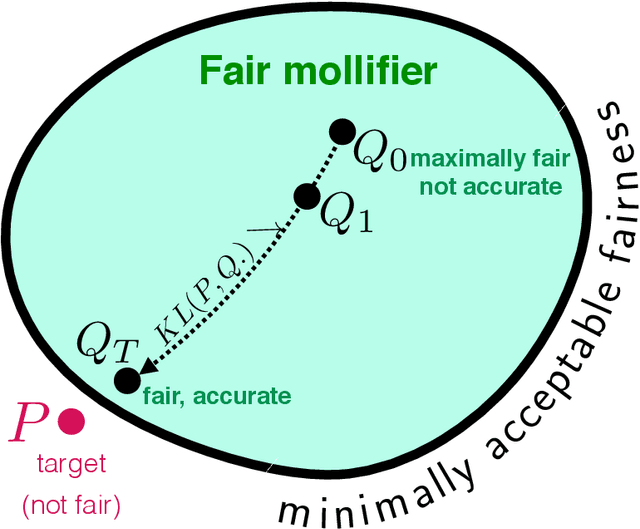
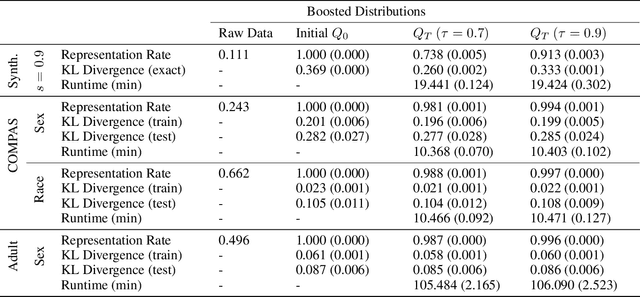
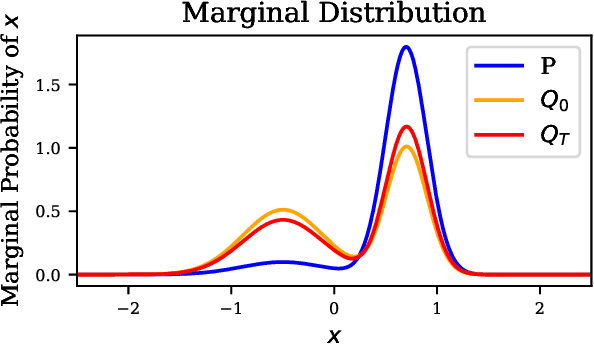
In a recent paper, Celis et al. (2020) introduced a new approach to fairness that corrects the data distribution itself. The approach is computationally appealing, but its approximation guarantees with respect to the target distribution can be quite loose as they need to rely on a (typically limited) number of constraints on data-based aggregated statistics; also resulting on a fairness guarantee which can be data dependent. Our paper makes use of a mathematical object recently introduced in privacy -- mollifiers of distributions -- and a popular approach to machine learning -- boosting -- to get an approach in the same lineage as Celis et al. but without those impediments, including in particular, better guarantees in terms of accuracy and finer guarantees in terms of fairness. The approach involves learning the sufficient statistics of an exponential family. When training data is tabular, it is defined by decision trees whose interpretability can provide clues on the source of (un)fairness. Experiments display the quality of the results obtained for simulated and real-world data.

Optimal Continual Learning has Perfect Memory and is NP-hard

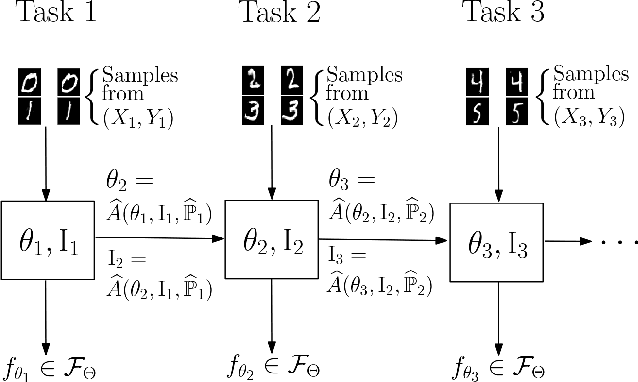
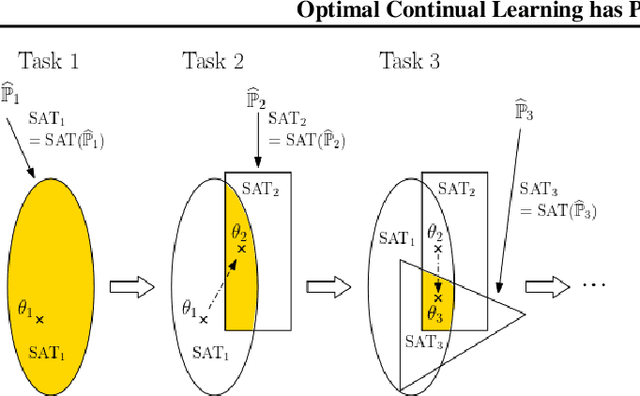
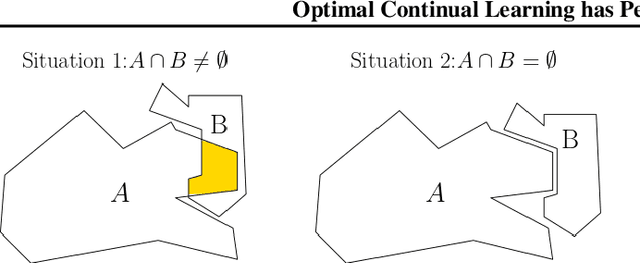
Continual Learning (CL) algorithms incrementally learn a predictor or representation across multiple sequentially observed tasks. Designing CL algorithms that perform reliably and avoid so-called catastrophic forgetting has proven a persistent challenge. The current paper develops a theoretical approach that explains why. In particular, we derive the computational properties which CL algorithms would have to possess in order to avoid catastrophic forgetting. Our main finding is that such optimal CL algorithms generally solve an NP-hard problem and will require perfect memory to do so. The findings are of theoretical interest, but also explain the excellent performance of CL algorithms using experience replay, episodic memory and core sets relative to regularization-based approaches.

Distributional Robustness with IPMs and links to Regularization and GANs

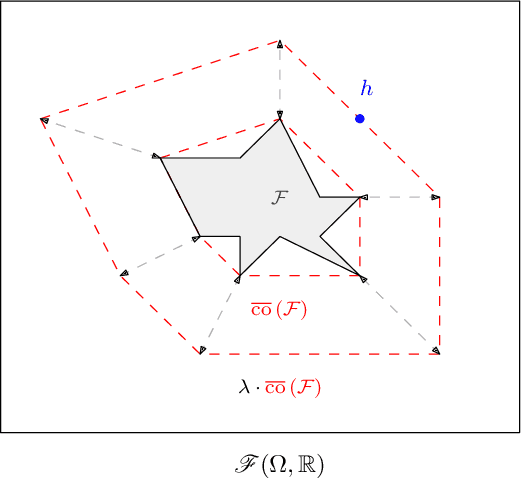
Robustness to adversarial attacks is an important concern due to the fragility of deep neural networks to small perturbations and has received an abundance of attention in recent years. Distributionally Robust Optimization (DRO), a particularly promising way of addressing this challenge, studies robustness via divergence-based uncertainty sets and has provided valuable insights into robustification strategies such as regularization. In the context of machine learning, the majority of existing results have chosen $f$-divergences, Wasserstein distances and more recently, the Maximum Mean Discrepancy (MMD) to construct uncertainty sets. We extend this line of work for the purposes of understanding robustness via regularization by studying uncertainty sets constructed with Integral Probability Metrics (IPMs) - a large family of divergences including the MMD, Total Variation and Wasserstein distances. Our main result shows that DRO under \textit{any} choice of IPM corresponds to a family of regularization penalties, which recover and improve upon existing results in the setting of MMD and Wasserstein distances. Due to the generality of our result, we show that other choices of IPMs correspond to other commonly used penalties in machine learning. Furthermore, we extend our results to shed light on adversarial generative modelling via $f$-GANs, constituting the first study of distributional robustness for the $f$-GAN objective. Our results unveil the inductive properties of the discriminator set with regards to robustness, allowing us to give positive comments for several penalty-based GAN methods such as Wasserstein-, MMD- and Sobolev-GANs. In summary, our results intimately link GANs to distributional robustness, extend previous results on DRO and contribute to our understanding of the link between regularization and robustness at large.