Generator Surgery for Compressed Sensing

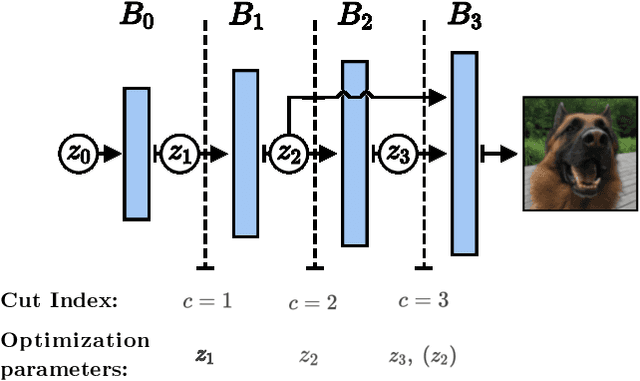
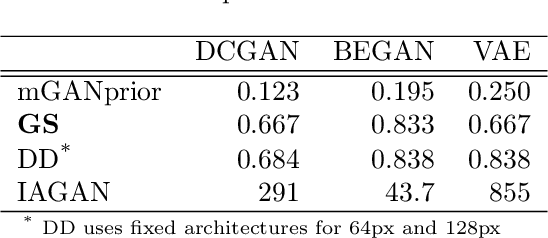
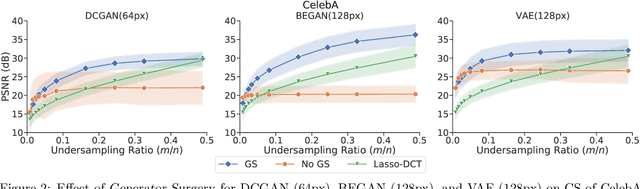
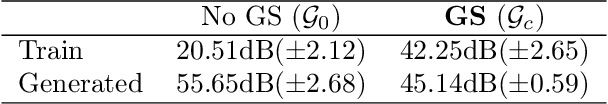
Image recovery from compressive measurements requires a signal prior for the images being reconstructed. Recent work has explored the use of deep generative models with low latent dimension as signal priors for such problems. However, their recovery performance is limited by high representation error. We introduce a method for achieving low representation error using generators as signal priors. Using a pre-trained generator, we remove one or more initial blocks at test time and optimize over the new, higher-dimensional latent space to recover a target image. Experiments demonstrate significantly improved reconstruction quality for a variety of network architectures. This approach also works well for out-of-training-distribution images and is competitive with other state-of-the-art methods. Our experiments show that test-time architectural modifications can greatly improve the recovery quality of generator signal priors for compressed sensing.

Meta-Learning Dynamics Forecasting Using Task Inference

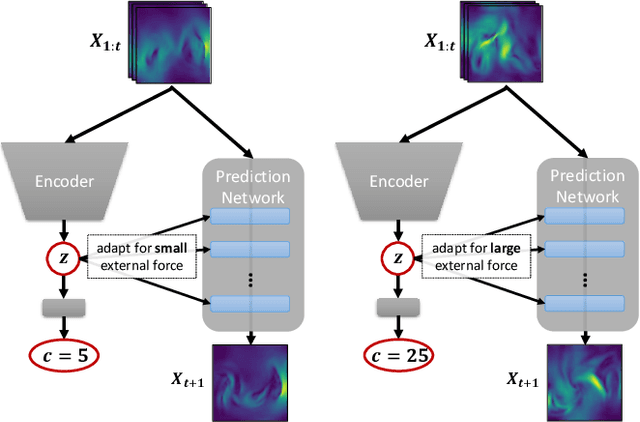
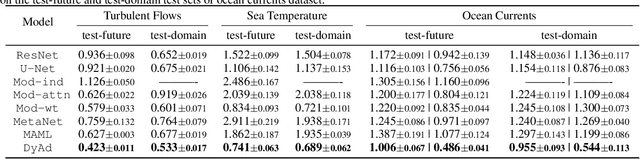
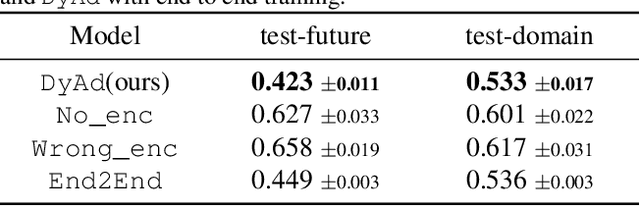
Current deep learning models for dynamics forecasting struggle with generalization. They can only forecast in a specific domain and fail when applied to systems with different parameters, external forces, or boundary conditions. We propose a model-based meta-learning method called DyAd which can generalize across heterogeneous domains by partitioning them into separate subdomains, each with a different task. DyAd has two parts: a prediction network which learns the shared dynamics of the entire domain, and an encoder that infers the parameters of the task. The encoder adapts the prediction network during inference time using adaptive instance normalization and a new layer, AdaPad, specifically designed for boundary conditions. The encoder can also use any weak supervision signals that can help distinguish different tasks, allowing the incorporation of additional domain knowledge. Our model outperforms a variety of state-of-the-art approaches on both turbulent flow and real-world ocean data forecasting tasks.

DeepGLEAM: a hybrid mechanistic and deep learning model for COVID-19 forecasting

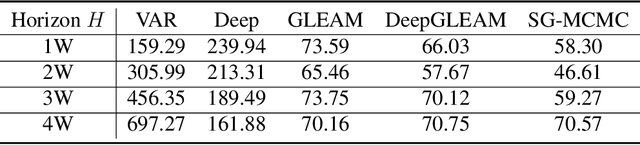
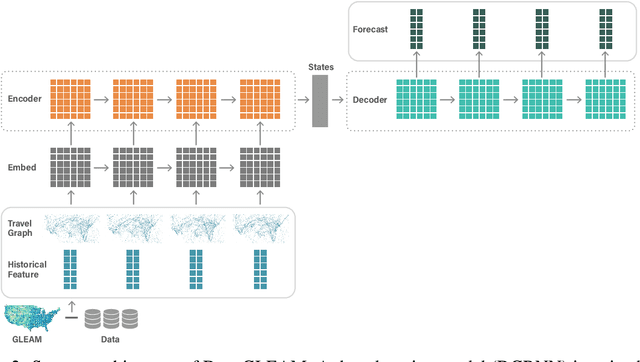
We introduce DeepGLEAM, a hybrid model for COVID-19 forecasting. DeepGLEAM combines a mechanistic stochastic simulation model GLEAM with deep learning. It uses deep learning to learn the correction terms from GLEAM, which leads to improved performance. We further integrate various uncertainty quantification methods to generate confidence intervals. We demonstrate DeepGLEAM on real-world COVID-19 mortality forecasting tasks.

Bridging Physics-based and Data-driven modeling for Learning Dynamical Systems

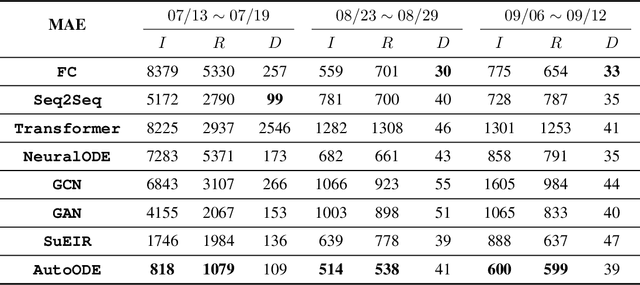
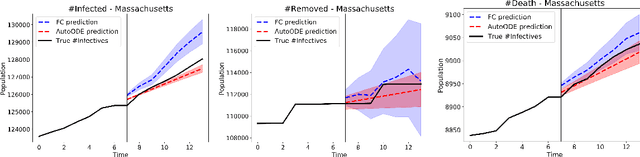
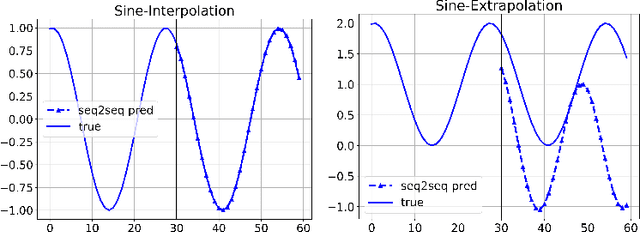
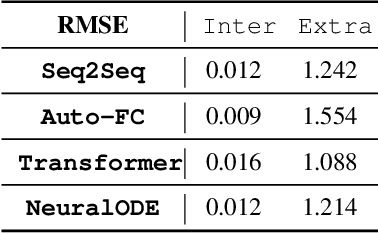
How can we learn a dynamical system to make forecasts, when some variables are unobserved? For instance, in COVID-19, we want to forecast the number of infected and death cases but we do not know the count of susceptible and exposed people. While mechanics compartment models are widely-used in epidemic modeling, data-driven models are emerging for disease forecasting. As a case study, we compare these two types of models for COVID-19 forecasting and notice that physics-based models significantly outperform deep learning models. We present a hybrid approach, AutoODE-COVID, which combines a novel compartmental model with automatic differentiation. Our method obtains a 57.4% reduction in mean absolute errors for 7-day ahead COVID-19 forecasting compared with the best deep learning competitor. To understand the inferior performance of deep learning, we investigate the generalization problem in forecasting. Through systematic experiments, we found that deep learning models fail to forecast under shifted distributions either in the data domain or the parameter domain. This calls attention to rethink generalization especially for learning dynamical systems.

Trajectory Prediction using Equivariant Continuous Convolution

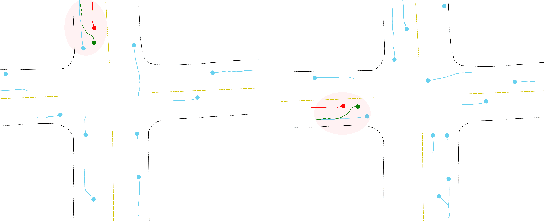
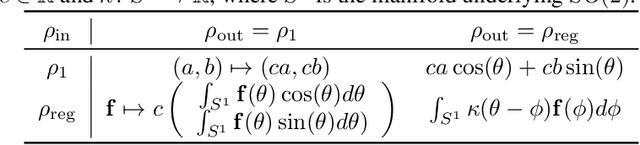
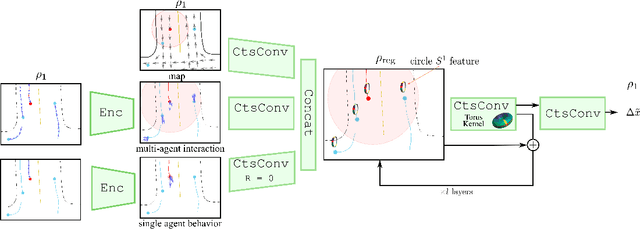
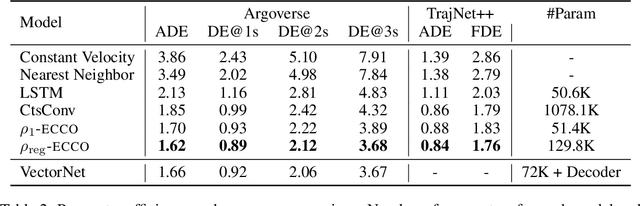
Trajectory prediction is a critical part of many AI applications, for example, the safe operation of autonomous vehicles. However, current methods are prone to making inconsistent and physically unrealistic predictions. We leverage insights from fluid dynamics to overcome this limitation by considering internal symmetry in trajectories. We propose a novel model, Equivariant Continous COnvolution (ECCO) for improved trajectory prediction. ECCO uses rotationally-equivariant continuous convolutions to embed the symmetries of the system. On two real-world vehicle and pedestrian trajectory datasets, ECCO attains competitive accuracy with significantly fewer parameters. It is also more sample efficient, generalizing automatically from few data points in any orientation. Lastly, ECCO improves generalization with equivariance, resulting in more physically consistent predictions. Our method provides a fresh perspective towards increasing trust and transparency in deep learning models.

Deep Imitation Learning for Bimanual Robotic Manipulation

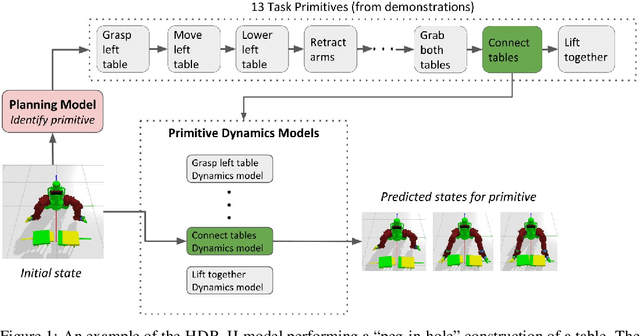
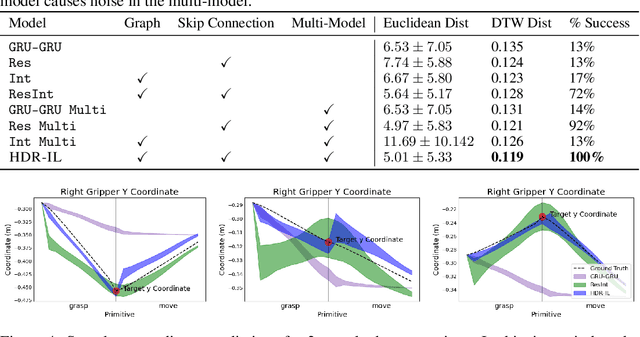
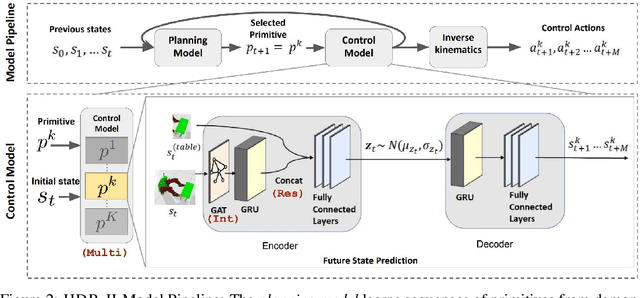
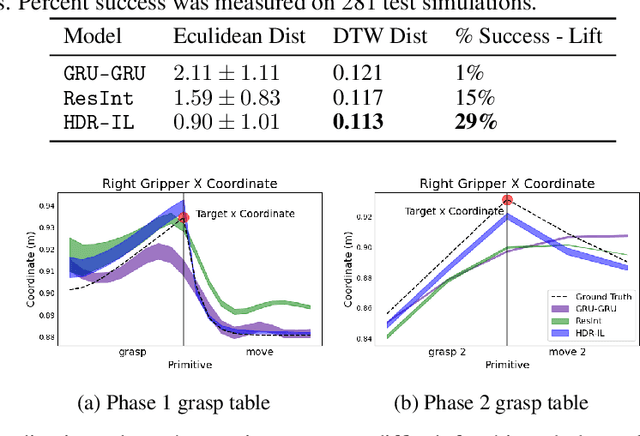
We present a deep imitation learning framework for robotic bimanual manipulation in a continuous state-action space. Imitation learning has been effectively utilized in mimicking bimanual manipulation movements, but generalizing the movement to objects in different locations has not been explored. We hypothesize that to precisely generalize the learned behavior relative to an object's location requires modeling relational information in the environment. To achieve this, we designed a method that (i) uses a multi-model framework to decomposes complex dynamics into elemental movement primitives, and (ii) parameterizes each primitive using a recurrent graph neural network to capture interactions. Our model is a deep, hierarchical, modular architecture with a high-level planner that learns to compose primitives sequentially and a low-level controller which integrates primitive dynamics modules and inverse kinematics control. We demonstrate the effectiveness using several simulated bimanual robotic manipulation tasks. Compared to models based on previous imitation learning studies, our model generalizes better and achieves higher success rates in the simulated tasks.

Dynamic Relational Inference in Multi-Agent Trajectories

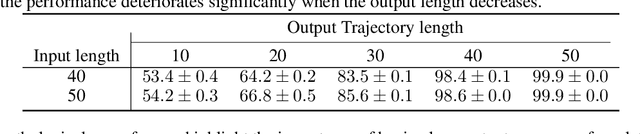
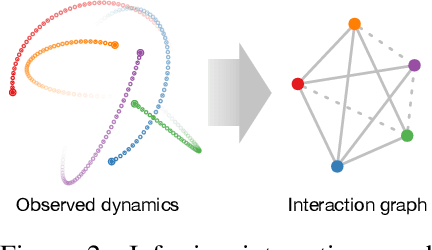
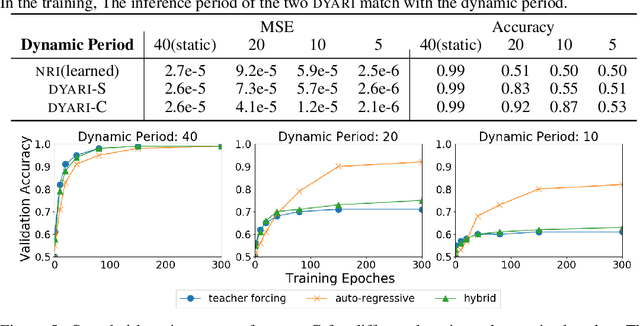
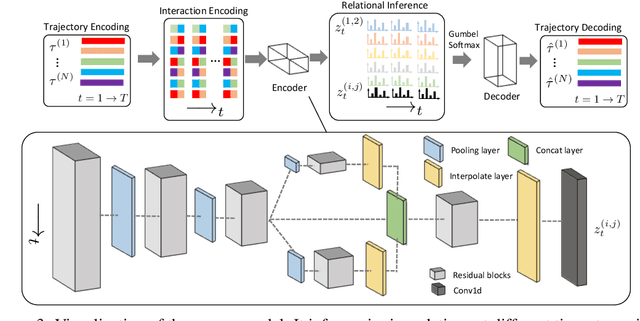
Inferring interactions from multi-agent trajectories has broad applications in physics, vision and robotics. Neural relational inference (NRI) is a deep generative model that can reason about relations in complex dynamics without supervision. In this paper, we take a careful look at this approach for relational inference in multi-agent trajectories. First, we discover that NRI can be fundamentally limited without sufficient long-term observations. Its ability to accurately infer interactions degrades drastically for short output sequences. Next, we consider a more general setting of relational inference when interactions are changing overtime. We propose an extension ofNRI, which we call the DYnamic multi-AgentRelational Inference (DYARI) model that can reason about dynamic relations. We conduct exhaustive experiments to study the effect of model architecture, under-lying dynamics and training scheme on the performance of dynamic relational inference using a simulated physics system. We also showcase the usage of our model on real-world multi-agent basketball trajectories.

Finding Patient Zero: Learning Contagion Source with Graph Neural Networks

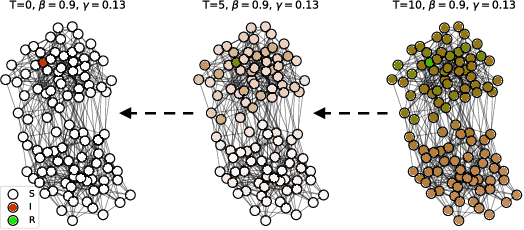
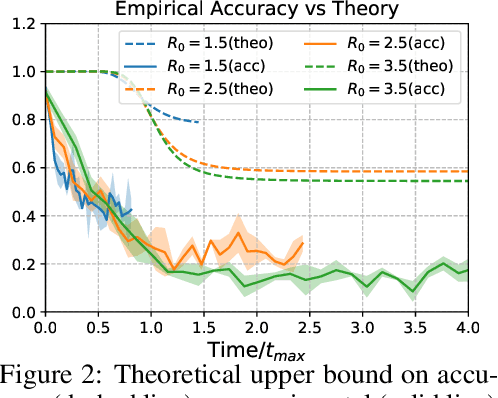
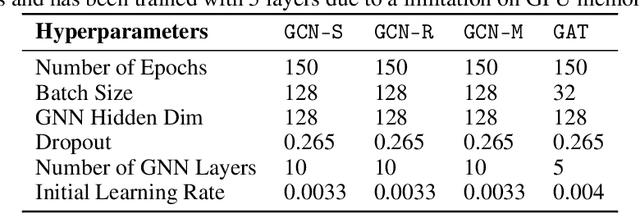
Locating the source of an epidemic, or patient zero (P0), can provide critical insights into the infection's transmission course and allow efficient resource allocation. Existing methods use graph-theoretic centrality measures and expensive message-passing algorithms, requiring knowledge of the underlying dynamics and its parameters. In this paper, we revisit this problem using graph neural networks (GNNs) to learn P0. We establish a theoretical limit for the identification of P0 in a class of epidemic models. We evaluate our method against different epidemic models on both synthetic and a real-world contact network considering a disease with history and characteristics of COVID-19. % We observe that GNNs can identify P0 close to the theoretical bound on accuracy, without explicit input of dynamics or its parameters. In addition, GNN is over 100 times faster than classic methods for inference on arbitrary graph topologies. Our theoretical bound also shows that the epidemic is like a ticking clock, emphasizing the importance of early contact-tracing. We find a maximum time after which accurate recovery of the source becomes impossible, regardless of the algorithm used.

Learning Disentangled Representations of Video with Missing Data

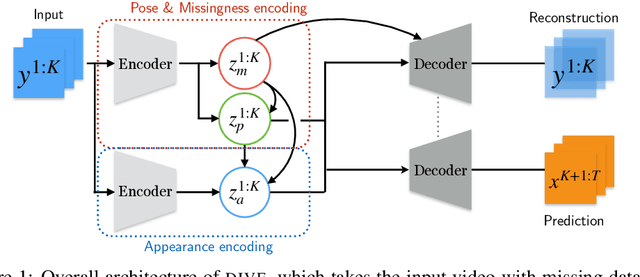
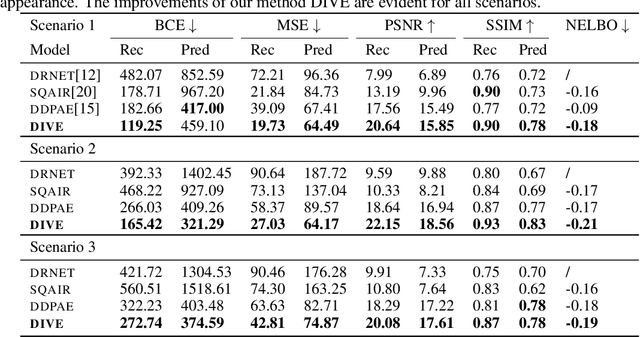
Missing data poses significant challenges while learning representations of video sequences. We present Disentangled Imputed Video autoEncoder (DIVE), a deep generative model that imputes and predicts future video frames in the presence of missing data. Specifically, DIVE introduces a missingness latent variable, disentangles the hidden video representations into static and dynamic appearance, pose, and missingness factors for each object, while it imputes each object trajectory where data is missing. On a moving MNIST dataset with various missing scenarios, DIVE outperforms the state of the art baselines by a substantial margin. We also present comparisons for real-world MOTSChallenge pedestrian dataset, which demonstrates the practical value of our method in a more realistic setting.

Aortic Pressure Forecasting with Deep Sequence Learning

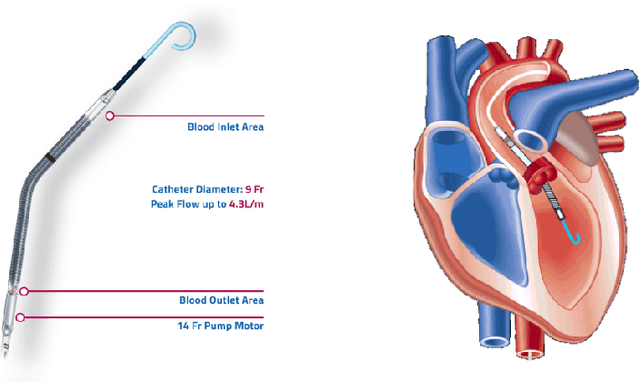
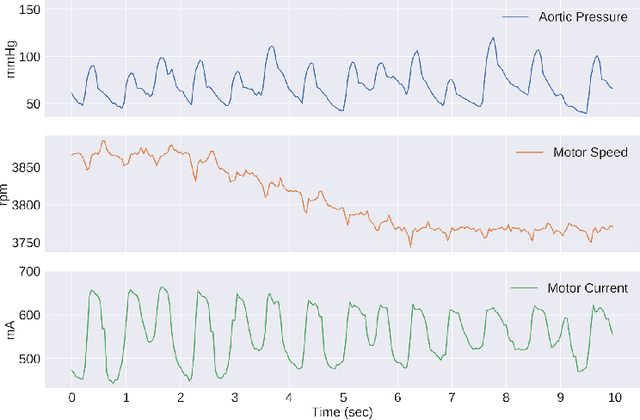
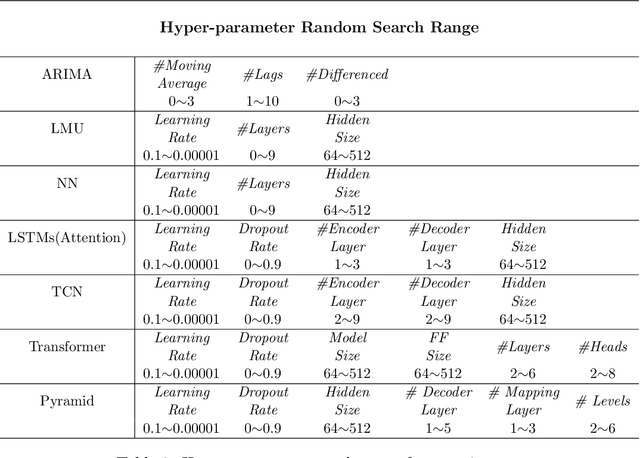
Mean aortic pressure is a major determinant of perfusion in all organ systems. The ability to forecast the mean aortic pressure would enhance the ability of physicians to estimate prognosis of the patient and assist in early detection of hemodynamic instability. However, forecasting aortic pressure is challenging because the blood pressure time series is noisy and can be highly non-stationary. In this study, we provided a benchmark study of different deep sequence learning models on pump performance data obtained in patients who underwent high-risk percutaneous intervention with transvalvular micro-axial heart pump support. The aim of this study was to forecast the mean aortic pressure five minutes in advance, using the time series data of previous five minutes as input. We performed comprehensive study on time series with increasing, decreasing, and stationary trends. The experiments show promising results with the Legendre Memory Unit architecture achieving the best performance with an overall RMSE of 1.837 mmHg.