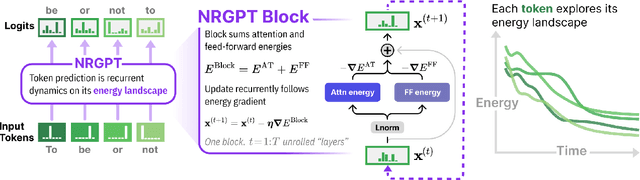
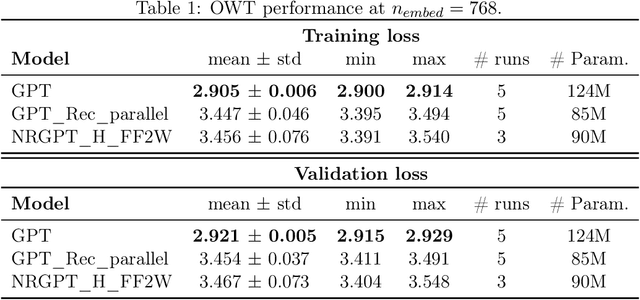
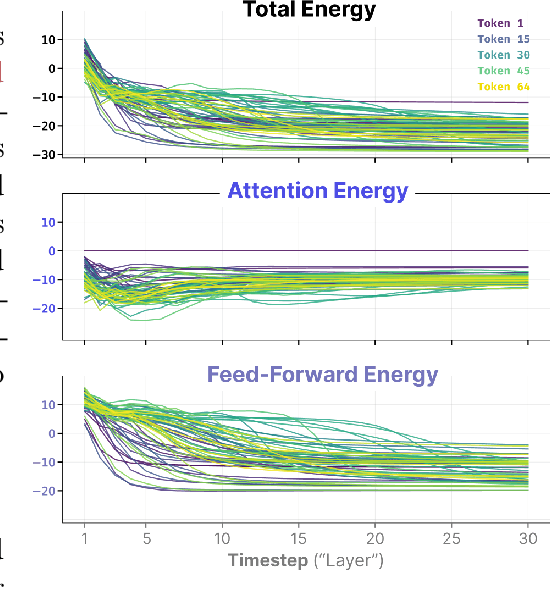
NRGPT: An Energy-based Alternative for GPT

Generative Pre-trained Transformer (GPT) architectures are the most popular design for language modeling. Energy-based modeling is a different paradigm that views inference as a dynamical process operating on an energy landscape. We propose a minimal modification of the GPT setting to unify it with the EBM framework. The inference step of our model, which we call eNeRgy-GPT (NRGPT), is conceptualized as an exploration of the tokens on the energy landscape. We prove, and verify empirically, that under certain circumstances this exploration becomes gradient descent, although they don't necessarily lead to the best performing models. We demonstrate that our model performs well for simple language (Shakespeare dataset), algebraic ListOPS tasks, and richer settings such as OpenWebText language modeling. We also observe that our models may be more resistant to overfitting, doing so only during very long training.

Understanding Mode Connectivity via Parameter Space Symmetry

Neural network minima are often connected by curves along which train and test loss remain nearly constant, a phenomenon known as mode connectivity. While this property has enabled applications such as model merging and fine-tuning, its theoretical explanation remains unclear. We propose a new approach to exploring the connectedness of minima using parameter space symmetry. By linking the topology of symmetry groups to that of the minima, we derive the number of connected components of the minima of linear networks and show that skip connections reduce this number. We then examine when mode connectivity and linear mode connectivity hold or fail, using parameter symmetries which account for a significant part of the minimum. Finally, we provide explicit expressions for connecting curves in the minima induced by symmetry. Using the curvature of these curves, we derive conditions under which linear mode connectivity approximately holds. Our findings highlight the role of continuous symmetries in understanding the neural network loss landscape.

Small Models, Smarter Learning: The Power of Joint Task Training

The ability of a model to learn a task depends strongly on both the task difficulty and the model size. We aim to understand how task difficulty relates to the minimum number of parameters required for learning specific tasks in small transformer models. Our study focuses on the ListOps dataset, which consists of nested mathematical operations. We gradually increase task difficulty by introducing new operations or combinations of operations into the training data. We observe that sum modulo n is the hardest to learn. Curiously, when combined with other operations such as maximum and median, the sum operation becomes easier to learn and requires fewer parameters. We show that joint training not only improves performance but also leads to qualitatively different model behavior. We show evidence that models trained only on SUM might be memorizing and fail to capture the number structure in the embeddings. In contrast, models trained on a mixture of SUM and other operations exhibit number-like representations in the embedding space, and a strong ability to distinguish parity. Furthermore, the SUM-only model relies more heavily on its feedforward layers, while the jointly trained model activates the attention mechanism more. Finally, we show that learning pure SUM can be induced in models below the learning threshold of pure SUM, by pretraining them on MAX+MED. Our findings indicate that emergent abilities in language models depend not only on model size, but also the training curriculum.

Discovering Symbolic Differential Equations with Symmetry Invariants

Discovering symbolic differential equations from data uncovers fundamental dynamical laws underlying complex systems. However, existing methods often struggle with the vast search space of equations and may produce equations that violate known physical laws. In this work, we address these problems by introducing the concept of \textit{symmetry invariants} in equation discovery. We leverage the fact that differential equations admitting a symmetry group can be expressed in terms of differential invariants of symmetry transformations. Thus, we propose to use these invariants as atomic entities in equation discovery, ensuring the discovered equations satisfy the specified symmetry. Our approach integrates seamlessly with existing equation discovery methods such as sparse regression and genetic programming, improving their accuracy and efficiency. We validate the proposed method through applications to various physical systems, such as fluid and reaction-diffusion, demonstrating its ability to recover parsimonious and interpretable equations that respect the laws of physics.

AtlasD: Automatic Local Symmetry Discovery

Existing symmetry discovery methods predominantly focus on global transformations across the entire system or space, but they fail to consider the symmetries in local neighborhoods. This may result in the reported symmetry group being a misrepresentation of the true symmetry. In this paper, we formalize the notion of local symmetry as atlas equivariance. Our proposed pipeline, automatic local symmetry discovery (AtlasD), recovers the local symmetries of a function by training local predictor networks and then learning a Lie group basis to which the predictors are equivariant. We demonstrate AtlasD is capable of discovering local symmetry groups with multiple connected components in top-quark tagging and partial differential equation experiments. The discovered local symmetry is shown to be a useful inductive bias that improves the performance of downstream tasks in climate segmentation and vision tasks.

Symmetry-Informed Governing Equation Discovery

Despite the advancements in learning governing differential equations from observations of dynamical systems, data-driven methods are often unaware of fundamental physical laws, such as frame invariance. As a result, these algorithms may search an unnecessarily large space and discover equations that are less accurate or overly complex. In this paper, we propose to leverage symmetry in automated equation discovery to compress the equation search space and improve the accuracy and simplicity of the learned equations. Specifically, we derive equivariance constraints from the time-independent symmetries of ODEs. Depending on the types of symmetries, we develop a pipeline for incorporating symmetry constraints into various equation discovery algorithms, including sparse regression and genetic programming. In experiments across a diverse range of dynamical systems, our approach demonstrates better robustness against noise and recovers governing equations with significantly higher probability than baselines without symmetry.

Latent Space Symmetry Discovery

Equivariant neural networks require explicit knowledge of the symmetry group. Automatic symmetry discovery methods aim to relax this constraint and learn invariance and equivariance from data. However, existing symmetry discovery methods are limited to linear symmetries in their search space and cannot handle the complexity of symmetries in real-world, often high-dimensional data. We propose a novel generative model, Latent LieGAN (LaLiGAN), which can discover nonlinear symmetries from data. It learns a mapping from data to a latent space where the symmetries become linear and simultaneously discovers symmetries in the latent space. Theoretically, we show that our method can express any nonlinear symmetry under certain conditions. Experimentally, our method can capture the intrinsic symmetry in high-dimensional observations, which results in a well-structured latent space that is useful for other downstream tasks. We demonstrate the use cases for LaLiGAN in improving equation discovery and long-term forecasting for various dynamical systems.

Generative Adversarial Symmetry Discovery

Despite the success of equivariant neural networks in scientific applications, they require knowing the symmetry group a priori. However, it may be difficult to know the right symmetry to use as an inductive bias in practice and enforcing the wrong symmetry could hurt the performance. In this paper, we propose a framework, LieGAN, to automatically discover equivariances from a dataset using a paradigm akin to generative adversarial training. Specifically, a generator learns a group of transformations applied to the data, which preserves the original distribution and fools the discriminator. LieGAN represents symmetry as interpretable Lie algebra basis and can discover various symmetries such as rotation group $\mathrm{SO}(n)$ and restricted Lorentz group $\mathrm{SO}(1,3)^+$ in trajectory prediction and top quark tagging tasks. The learned symmetry can also be readily used in several existing equivariant neural networks to improve accuracy and generalization in prediction.

Symmetries, flat minima, and the conserved quantities of gradient flow

Empirical studies of the loss landscape of deep networks have revealed that many local minima are connected through low-loss valleys. Ensemble models sampling different parts of a low-loss valley have reached SOTA performance. Yet, little is known about the theoretical origin of such valleys. We present a general framework for finding continuous symmetries in the parameter space, which carve out low-loss valleys. Importantly, we introduce a novel set of nonlinear, data-dependent symmetries for neural networks. These symmetries can transform a trained model such that it performs similarly on new samples. We then show that conserved quantities associated with linear symmetries can be used to define coordinates along low-loss valleys. The conserved quantities help reveal that using common initialization methods, gradient flow only explores a small part of the global minimum. By relating conserved quantities to convergence rate and sharpness of the minimum, we provide insights on how initialization impacts convergence and generalizability. We also find the nonlinear action to be viable for ensemble building to improve robustness under certain adversarial attacks.

Faster Optimization on Sparse Graphs via Neural Reparametrization

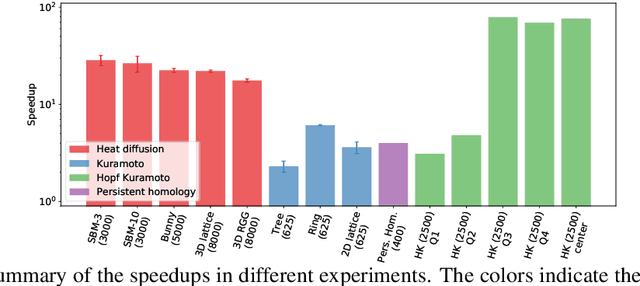
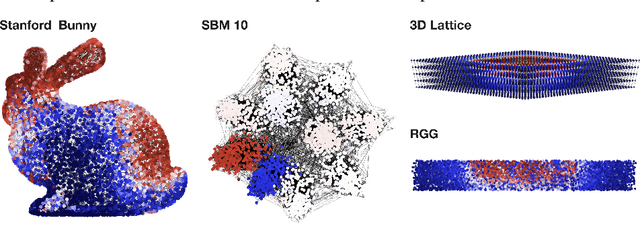
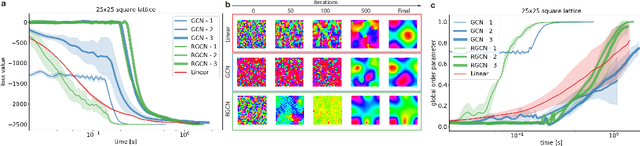
In mathematical optimization, second-order Newton's methods generally converge faster than first-order methods, but they require the inverse of the Hessian, hence are computationally expensive. However, we discover that on sparse graphs, graph neural networks (GNN) can implement an efficient Quasi-Newton method that can speed up optimization by a factor of 10-100x. Our method, neural reparametrization, modifies the optimization parameters as the output of a GNN to reshape the optimization landscape. Using a precomputed Hessian as the propagation rule, the GNN can effectively utilize the second-order information, reaching a similar effect as adaptive gradient methods. As our method solves optimization through architecture design, it can be used in conjunction with any optimizers such as Adam and RMSProp. We show the application of our method on scientifically relevant problems including heat diffusion, synchronization and persistent homology.