Improving Convergence and Generalization Using Parameter Symmetries

In overparametrized models, different values of the parameters may result in the same loss value. Parameter space symmetries are transformations that change the model parameters but leave the loss invariant. Teleportation applies such transformations to accelerate optimization. However, the exact mechanism behind this algorithm's success is not well understood. In this paper, we show that teleportation not only speeds up optimization in the short-term, but gives overall faster time to convergence. Additionally, we show that teleporting to minima with different curvatures improves generalization and provide insights on the connection between the curvature of the minima and generalization ability. Finally, we show that integrating teleportation into a wide range of optimization algorithms and optimization-based meta-learning improves convergence.

Disentangled Multi-Fidelity Deep Bayesian Active Learning

To balance quality and cost, various domain areas of science and engineering run simulations at multiple levels of sophistication. Multi-fidelity active learning aims to learn a direct mapping from input parameters to simulation outputs by actively acquiring data from multiple fidelity levels. However, existing approaches based on Gaussian processes are hardly scalable to high-dimensional data. Other deep learning-based methods use the hierarchical structure, which only supports passing information from low-fidelity to high-fidelity. This approach also leads to the undesirable propagation of errors from low-fidelity representations to high-fidelity ones. We propose a novel disentangled deep Bayesian learning framework for multi-fidelity active learning, that learns the surrogate models conditioned on the distribution of functions at multiple fidelities.

Long-term Forecasting with TiDE: Time-series Dense Encoder

Recent work has shown that simple linear models can outperform several Transformer based approaches in long term time-series forecasting. Motivated by this, we propose a Multi-layer Perceptron (MLP) based encoder-decoder model, Time-series Dense Encoder (TiDE), for long-term time-series forecasting that enjoys the simplicity and speed of linear models while also being able to handle covariates and non-linear dependencies. Theoretically, we prove that the simplest linear analogue of our model can achieve near optimal error rate for linear dynamical systems (LDS) under some assumptions. Empirically, we show that our method can match or outperform prior approaches on popular long-term time-series forecasting benchmarks while being 5-10x faster than the best Transformer based model.

Understanding why shooters shoot -- An AI-powered engine for basketball performance profiling

Understanding player shooting profiles is an essential part of basketball analysis: knowing where certain opposing players like to shoot from can help coaches neutralize offensive gameplans from their opponents; understanding where their players are most comfortable can lead them to developing more effective offensive strategies. An automatic tool that can provide these performance profiles in a timely manner can become invaluable for coaches to maximize both the effectiveness of their game plan as well as the time dedicated to practice and other related activities. Additionally, basketball is dictated by many variables, such as playstyle and game dynamics, that can change the flow of the game and, by extension, player performance profiles. It is crucial that the performance profiles can reflect the diverse playstyles, as well as the fast-changing dynamics of the game. We present a tool that can visualize player performance profiles in a timely manner while taking into account factors such as play-style and game dynamics. Our approach generates interpretable heatmaps that allow us to identify and analyze how non-spatial factors, such as game dynamics or playstyle, affect player performance profiles.

Generative Adversarial Symmetry Discovery

Despite the success of equivariant neural networks in scientific applications, they require knowing the symmetry group a priori. However, it may be difficult to know the right symmetry to use as an inductive bias in practice and enforcing the wrong symmetry could hurt the performance. In this paper, we propose a framework, LieGAN, to automatically discover equivariances from a dataset using a paradigm akin to generative adversarial training. Specifically, a generator learns a group of transformations applied to the data, which preserves the original distribution and fools the discriminator. LieGAN represents symmetry as interpretable Lie algebra basis and can discover various symmetries such as rotation group $\mathrm{SO}(n)$ and restricted Lorentz group $\mathrm{SO}(1,3)^+$ in trajectory prediction and top quark tagging tasks. The learned symmetry can also be readily used in several existing equivariant neural networks to improve accuracy and generalization in prediction.

On the Connection Between MPNN and Graph Transformer

Graph Transformer (GT) recently has emerged as a new paradigm of graph learning algorithms, outperforming the previously popular Message Passing Neural Network (MPNN) on multiple benchmarks. Previous work (Kim et al., 2022) shows that with proper position embedding, GT can approximate MPNN arbitrarily well, implying that GT is at least as powerful as MPNN. In this paper, we study the inverse connection and show that MPNN with virtual node (VN), a commonly used heuristic with little theoretical understanding, is powerful enough to arbitrarily approximate the self-attention layer of GT. In particular, we first show that if we consider one type of linear transformer, the so-called Performer/Linear Transformer (Choromanski et al., 2020; Katharopoulos et al., 2020), then MPNN + VN with only O(1) depth and O(1) width can approximate a self-attention layer in Performer/Linear Transformer. Next, via a connection between MPNN + VN and DeepSets, we prove the MPNN + VN with O(n^d) width and O(1) depth can approximate the self-attention layer arbitrarily well, where d is the input feature dimension. Lastly, under some assumptions, we provide an explicit construction of MPNN + VN with O(1) width and O(n) depth approximating the self-attention layer in GT arbitrarily well. On the empirical side, we demonstrate that 1) MPNN + VN is a surprisingly strong baseline, outperforming GT on the recently proposed Long Range Graph Benchmark (LRGB) dataset, 2) our MPNN + VN improves over early implementation on a wide range of OGB datasets and 3) MPNN + VN outperforms Linear Transformer and MPNN on the climate modeling task.

Copula Conformal Prediction for Multi-step Time Series Forecasting

Accurate uncertainty measurement is a key step to building robust and reliable machine learning systems. Conformal prediction is a distribution-free uncertainty quantification algorithm popular for its ease of implementation, statistical coverage guarantees, and versatility for underlying forecasters. However, existing conformal prediction algorithms for time series are limited to single-step prediction without considering the temporal dependency. In this paper we propose a Copula Conformal Prediction algorithm for multivariate, multi-step Time Series forecasting, CopulaCPTS. On several synthetic and real-world multivariate time series datasets, we show that CopulaCPTS produces more calibrated and sharp confidence intervals for multi-step prediction tasks than existing techniques.

Symmetries, flat minima, and the conserved quantities of gradient flow

Empirical studies of the loss landscape of deep networks have revealed that many local minima are connected through low-loss valleys. Ensemble models sampling different parts of a low-loss valley have reached SOTA performance. Yet, little is known about the theoretical origin of such valleys. We present a general framework for finding continuous symmetries in the parameter space, which carve out low-loss valleys. Importantly, we introduce a novel set of nonlinear, data-dependent symmetries for neural networks. These symmetries can transform a trained model such that it performs similarly on new samples. We then show that conserved quantities associated with linear symmetries can be used to define coordinates along low-loss valleys. The conserved quantities help reveal that using common initialization methods, gradient flow only explores a small part of the global minimum. By relating conserved quantities to convergence rate and sharpness of the minimum, we provide insights on how initialization impacts convergence and generalizability. We also find the nonlinear action to be viable for ensemble building to improve robustness under certain adversarial attacks.

Koopman Neural Forecaster for Time Series with Temporal Distribution Shifts

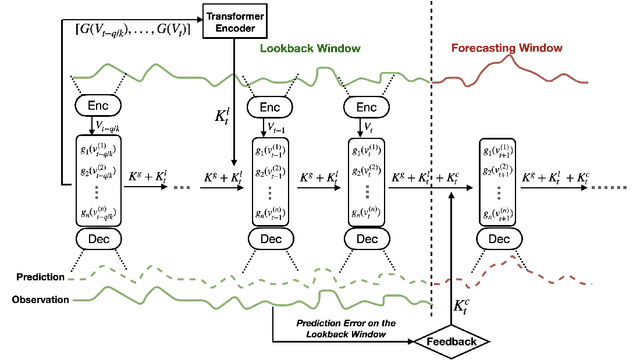
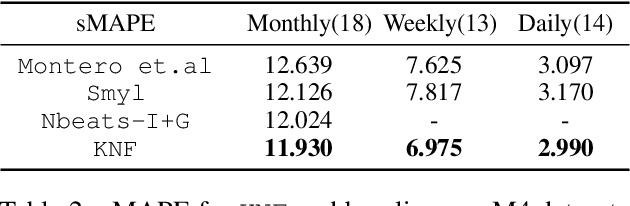
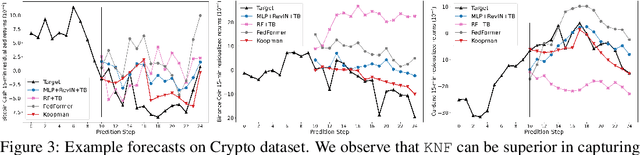
Temporal distributional shifts, with underlying dynamics changing over time, frequently occur in real-world time series, and pose a fundamental challenge for deep neural networks (DNNs). In this paper, we propose a novel deep sequence model based on the Koopman theory for time series forecasting: Koopman Neural Forecaster (KNF) that leverages DNNs to learn the linear Koopman space and the coefficients of chosen measurement functions. KNF imposes appropriate inductive biases for improved robustness against distributional shifts, employing both a global operator to learn shared characteristics, and a local operator to capture changing dynamics, as well as a specially-designed feedback loop to continuously update the learnt operators over time for rapidly varying behaviors. To the best of our knowledge, this is the first time that Koopman theory is applied to real-world chaotic time series without known governing laws. We demonstrate that KNF achieves the superior performance compared to the alternatives, on multiple time series datasets that are shown to suffer from distribution shifts.

Predicting the Future of AI with AI: High-quality link prediction in an exponentially growing knowledge network

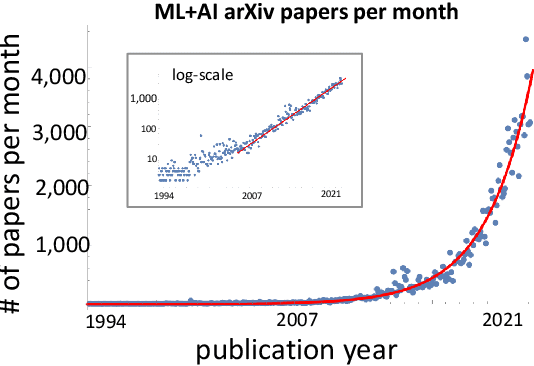
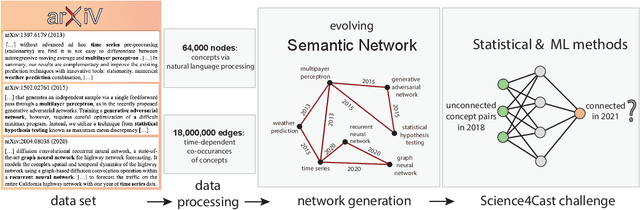
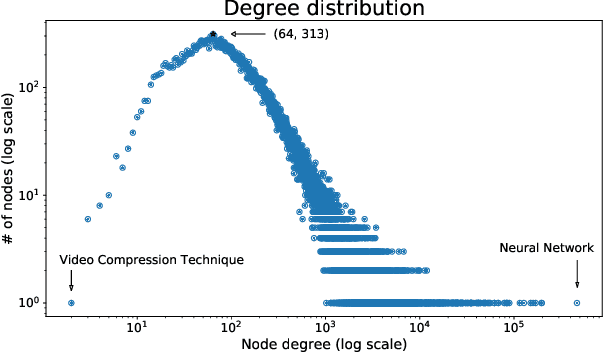
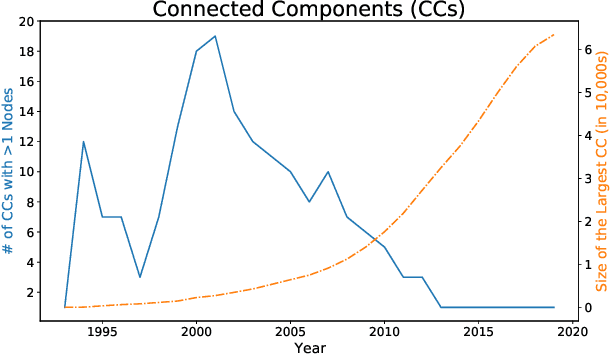
A tool that could suggest new personalized research directions and ideas by taking insights from the scientific literature could significantly accelerate the progress of science. A field that might benefit from such an approach is artificial intelligence (AI) research, where the number of scientific publications has been growing exponentially over the last years, making it challenging for human researchers to keep track of the progress. Here, we use AI techniques to predict the future research directions of AI itself. We develop a new graph-based benchmark based on real-world data -- the Science4Cast benchmark, which aims to predict the future state of an evolving semantic network of AI. For that, we use more than 100,000 research papers and build up a knowledge network with more than 64,000 concept nodes. We then present ten diverse methods to tackle this task, ranging from pure statistical to pure learning methods. Surprisingly, the most powerful methods use a carefully curated set of network features, rather than an end-to-end AI approach. It indicates a great potential that can be unleashed for purely ML approaches without human knowledge. Ultimately, better predictions of new future research directions will be a crucial component of more advanced research suggestion tools.