Non-Convex Matrix Completion Against a Semi-Random Adversary

Matrix completion is a well-studied problem with many machine learning applications. In practice, the problem is often solved by non-convex optimization algorithms. However, the current theoretical analysis for non-convex algorithms relies heavily on the assumption that every entry is observed with exactly the same probability $p$, which is not realistic in practice. In this paper, we investigate a more realistic semi-random model, where the probability of observing each entry is at least $p$. Even with this mild semi-random perturbation, we can construct counter-examples where existing non-convex algorithms get stuck in bad local optima. In light of the negative results, we propose a pre-processing step that tries to re-weight the semi-random input, so that it becomes "similar" to a random input. We give a nearly-linear time algorithm for this problem, and show that after our pre-processing, all the local minima of the non-convex objective can be used to approximately recover the underlying ground-truth matrix.

Matrix Completion has No Spurious Local Minimum

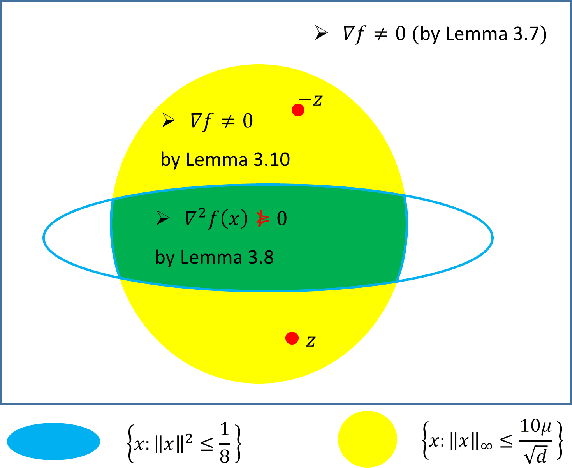
Matrix completion is a basic machine learning problem that has wide applications, especially in collaborative filtering and recommender systems. Simple non-convex optimization algorithms are popular and effective in practice. Despite recent progress in proving various non-convex algorithms converge from a good initial point, it remains unclear why random or arbitrary initialization suffices in practice. We prove that the commonly used non-convex objective function for \textit{positive semidefinite} matrix completion has no spurious local minima --- all local minima must also be global. Therefore, many popular optimization algorithms such as (stochastic) gradient descent can provably solve positive semidefinite matrix completion with \textit{arbitrary} initialization in polynomial time. The result can be generalized to the setting when the observed entries contain noise. We believe that our main proof strategy can be useful for understanding geometric properties of other statistical problems involving partial or noisy observations.

Beyond Log-concavity: Provable Guarantees for Sampling Multi-modal Distributions using Simulated Tempering Langevin Monte Carlo

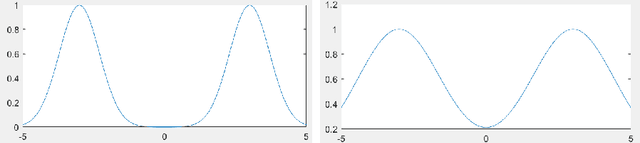
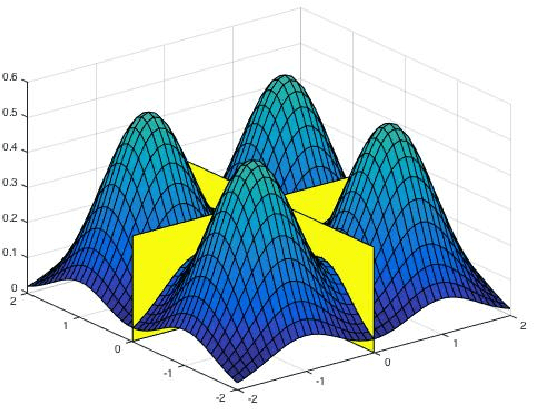
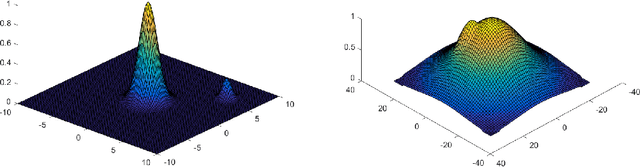
A key task in Bayesian statistics is sampling from distributions that are only specified up to a partition function (i.e., constant of proportionality). However, without any assumptions, sampling (even approximately) can be #P-hard, and few works have provided "beyond worst-case" guarantees for such settings. For log-concave distributions, classical results going back to Bakry and \'Emery (1985) show that natural continuous-time Markov chains called Langevin diffusions mix in polynomial time. The most salient feature of log-concavity violated in practice is uni-modality: commonly, the distributions we wish to sample from are multi-modal. In the presence of multiple deep and well-separated modes, Langevin diffusion suffers from torpid mixing. We address this problem by combining Langevin diffusion with simulated tempering. The result is a Markov chain that mixes more rapidly by transitioning between different temperatures of the distribution. We analyze this Markov chain for the canonical multi-modal distribution: a mixture of gaussians (of equal variance). The algorithm based on our Markov chain provably samples from distributions that are close to mixtures of gaussians, given access to the gradient of the log-pdf. For the analysis, we use a spectral decomposition theorem for graphs (Gharan and Trevisan, 2014) and a Markov chain decomposition technique (Madras and Randall, 2002).

Learning One-hidden-layer Neural Networks with Landscape Design

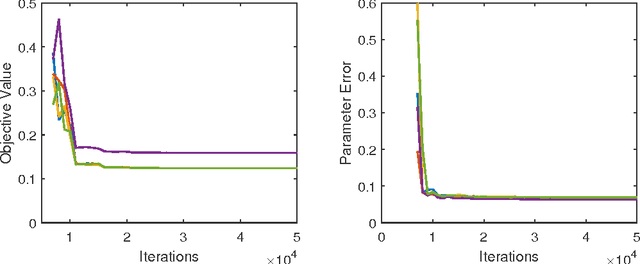
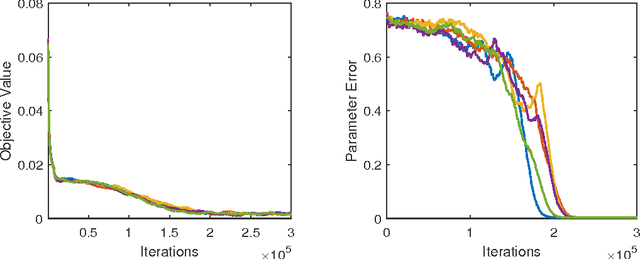
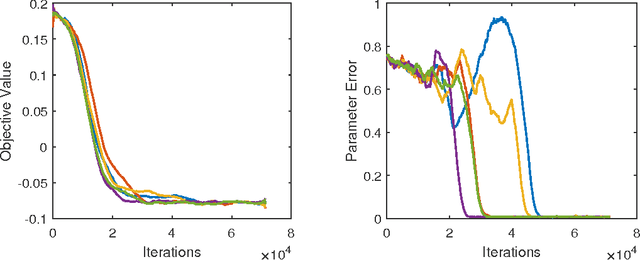
We consider the problem of learning a one-hidden-layer neural network: we assume the input $x\in \mathbb{R}^d$ is from Gaussian distribution and the label $y = a^\top \sigma(Bx) + \xi$, where $a$ is a nonnegative vector in $\mathbb{R}^m$ with $m\le d$, $B\in \mathbb{R}^{m\times d}$ is a full-rank weight matrix, and $\xi$ is a noise vector. We first give an analytic formula for the population risk of the standard squared loss and demonstrate that it implicitly attempts to decompose a sequence of low-rank tensors simultaneously. Inspired by the formula, we design a non-convex objective function $G(\cdot)$ whose landscape is guaranteed to have the following properties: 1. All local minima of $G$ are also global minima. 2. All global minima of $G$ correspond to the ground truth parameters. 3. The value and gradient of $G$ can be estimated using samples. With these properties, stochastic gradient descent on $G$ provably converges to the global minimum and learn the ground-truth parameters. We also prove finite sample complexity result and validate the results by simulations.

Generalization and Equilibrium in Generative Adversarial Nets (GANs)

We show that training of generative adversarial network (GAN) may not have good generalization properties; e.g., training may appear successful but the trained distribution may be far from target distribution in standard metrics. However, generalization does occur for a weaker metric called neural net distance. It is also shown that an approximate pure equilibrium exists in the discriminator/generator game for a special class of generators with natural training objectives when generator capacity and training set sizes are moderate. This existence of equilibrium inspires MIX+GAN protocol, which can be combined with any existing GAN training, and empirically shown to improve some of them.

On the Optimization Landscape of Tensor Decompositions

Non-convex optimization with local search heuristics has been widely used in machine learning, achieving many state-of-art results. It becomes increasingly important to understand why they can work for these NP-hard problems on typical data. The landscape of many objective functions in learning has been conjectured to have the geometric property that "all local optima are (approximately) global optima", and thus they can be solved efficiently by local search algorithms. However, establishing such property can be very difficult. In this paper, we analyze the optimization landscape of the random over-complete tensor decomposition problem, which has many applications in unsupervised learning, especially in learning latent variable models. In practice, it can be efficiently solved by gradient ascent on a non-convex objective. We show that for any small constant $\epsilon > 0$, among the set of points with function values $(1+\epsilon)$-factor larger than the expectation of the function, all the local maxima are approximate global maxima. Previously, the best-known result only characterizes the geometry in small neighborhoods around the true components. Our result implies that even with an initialization that is barely better than the random guess, the gradient ascent algorithm is guaranteed to solve this problem. Our main technique uses Kac-Rice formula and random matrix theory. To our best knowledge, this is the first time when Kac-Rice formula is successfully applied to counting the number of local minima of a highly-structured random polynomial with dependent coefficients.

Homotopy Analysis for Tensor PCA

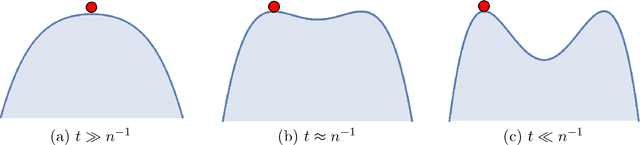
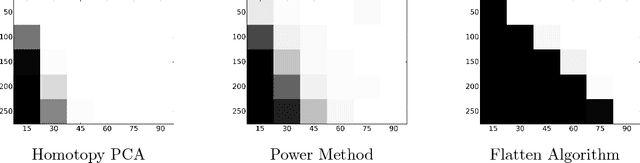
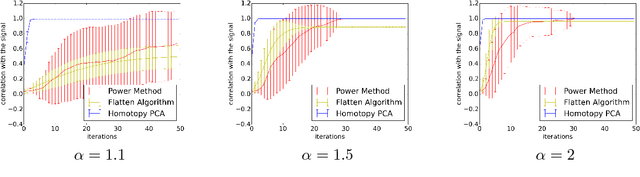
Developing efficient and guaranteed nonconvex algorithms has been an important challenge in modern machine learning. Algorithms with good empirical performance such as stochastic gradient descent often lack theoretical guarantees. In this paper, we analyze the class of homotopy or continuation methods for global optimization of nonconvex functions. These methods start from an objective function that is efficient to optimize (e.g. convex), and progressively modify it to obtain the required objective, and the solutions are passed along the homotopy path. For the challenging problem of tensor PCA, we prove global convergence of the homotopy method in the "high noise" regime. The signal-to-noise requirement for our algorithm is tight in the sense that it matches the recovery guarantee for the best degree-4 sum-of-squares algorithm. In addition, we prove a phase transition along the homotopy path for tensor PCA. This allows to simplify the homotopy method to a local search algorithm, viz., tensor power iterations, with a specific initialization and a noise injection procedure, while retaining the theoretical guarantees.

On the ability of neural nets to express distributions

Deep neural nets have caused a revolution in many classification tasks. A related ongoing revolution---also theoretically not understood---concerns their ability to serve as generative models for complicated types of data such as images and texts. These models are trained using ideas like variational autoencoders and Generative Adversarial Networks. We take a first cut at explaining the expressivity of multilayer nets by giving a sufficient criterion for a function to be approximable by a neural network with $n$ hidden layers. A key ingredient is Barron's Theorem \cite{Barron1993}, which gives a Fourier criterion for approximability of a function by a neural network with 1 hidden layer. We show that a composition of $n$ functions which satisfy certain Fourier conditions ("Barron functions") can be approximated by a $n+1$-layer neural network. For probability distributions, this translates into a criterion for a probability distribution to be approximable in Wasserstein distance---a natural metric on probability distributions---by a neural network applied to a fixed base distribution (e.g., multivariate gaussian). Building up recent lower bound work, we also give an example function that shows that composition of Barron functions is more expressive than Barron functions alone.

No Spurious Local Minima in Nonconvex Low Rank Problems: A Unified Geometric Analysis

In this paper we develop a new framework that captures the common landscape underlying the common non-convex low-rank matrix problems including matrix sensing, matrix completion and robust PCA. In particular, we show for all above problems (including asymmetric cases): 1) all local minima are also globally optimal; 2) no high-order saddle points exists. These results explain why simple algorithms such as stochastic gradient descent have global converge, and efficiently optimize these non-convex objective functions in practice. Our framework connects and simplifies the existing analyses on optimization landscapes for matrix sensing and symmetric matrix completion. The framework naturally leads to new results for asymmetric matrix completion and robust PCA.

How to Escape Saddle Points Efficiently

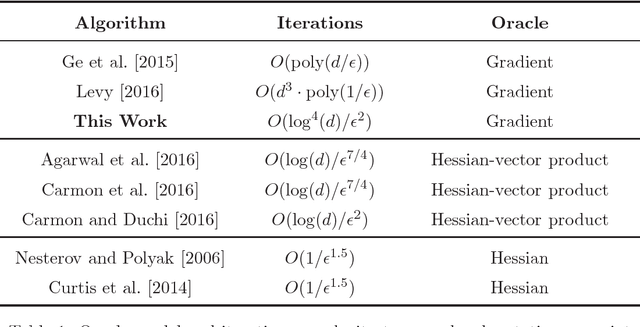
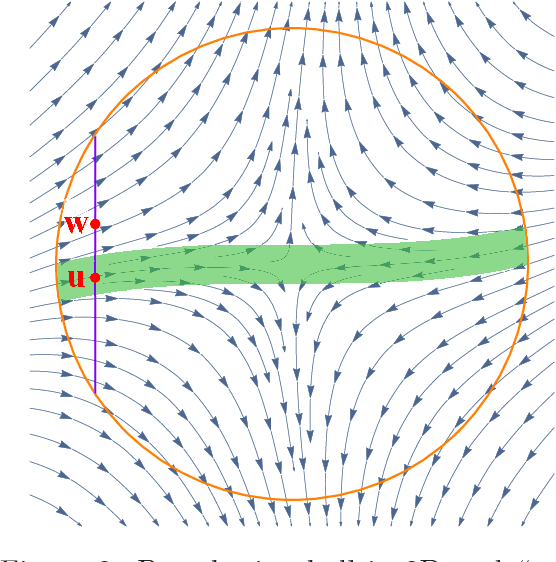
This paper shows that a perturbed form of gradient descent converges to a second-order stationary point in a number iterations which depends only poly-logarithmically on dimension (i.e., it is almost "dimension-free"). The convergence rate of this procedure matches the well-known convergence rate of gradient descent to first-order stationary points, up to log factors. When all saddle points are non-degenerate, all second-order stationary points are local minima, and our result thus shows that perturbed gradient descent can escape saddle points almost for free. Our results can be directly applied to many machine learning applications, including deep learning. As a particular concrete example of such an application, we show that our results can be used directly to establish sharp global convergence rates for matrix factorization. Our results rely on a novel characterization of the geometry around saddle points, which may be of independent interest to the non-convex optimization community.