Ricky T. Q. Chen
Riemannian Flow Matching on General Geometries
Feb 07, 2023Abstract:We propose Riemannian Flow Matching (RFM), a simple yet powerful framework for training continuous normalizing flows on manifolds. Existing methods for generative modeling on manifolds either require expensive simulation, inherently cannot scale to high dimensions, or use approximations to limiting quantities that result in biased objectives. Riemannian Flow Matching bypasses these inconveniences and exhibits multiple benefits over prior approaches: It is completely simulation-free on simple geometries, it does not require divergence computation, and its target vector field is computed in closed form even on general geometries. The key ingredient behind RFM is the construction of a simple kernel function for defining per-sample vector fields, which subsumes existing Euclidean cases. Extending to general geometries, we rely on the use of spectral decompositions to efficiently compute kernel functions. Our method achieves state-of-the-art performance on real-world non-Euclidean datasets, and we showcase, for the first time, tractable training on general geometries, including on triangular meshes and maze-like manifolds with boundaries.
Latent Discretization for Continuous-time Sequence Compression
Dec 28, 2022



Abstract:Neural compression offers a domain-agnostic approach to creating codecs for lossy or lossless compression via deep generative models. For sequence compression, however, most deep sequence models have costs that scale with the sequence length rather than the sequence complexity. In this work, we instead treat data sequences as observations from an underlying continuous-time process and learn how to efficiently discretize while retaining information about the full sequence. As a consequence of decoupling sequential information from its temporal discretization, our approach allows for greater compression rates and smaller computational complexity. Moreover, the continuous-time approach naturally allows us to decode at different time intervals. We empirically verify our approach on multiple domains involving compression of video and motion capture sequences, showing that our approaches can automatically achieve reductions in bit rates by learning how to discretize.
Flow Matching for Generative Modeling
Oct 06, 2022
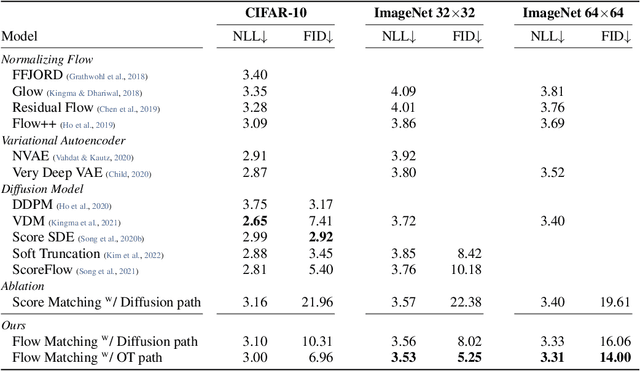

Abstract:We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching (FM), a simulation-free approach for training CNFs based on regressing vector fields of fixed conditional probability paths. Flow Matching is compatible with a general family of Gaussian probability paths for transforming between noise and data samples -- which subsumes existing diffusion paths as specific instances. Interestingly, we find that employing FM with diffusion paths results in a more robust and stable alternative for training diffusion models. Furthermore, Flow Matching opens the door to training CNFs with other, non-diffusion probability paths. An instance of particular interest is using Optimal Transport (OT) displacement interpolation to define the conditional probability paths. These paths are more efficient than diffusion paths, provide faster training and sampling, and result in better generalization. Training CNFs using Flow Matching on ImageNet leads to state-of-the-art performance in terms of both likelihood and sample quality, and allows fast and reliable sample generation using off-the-shelf numerical ODE solvers.
Neural Conservation Laws: A Divergence-Free Perspective
Oct 04, 2022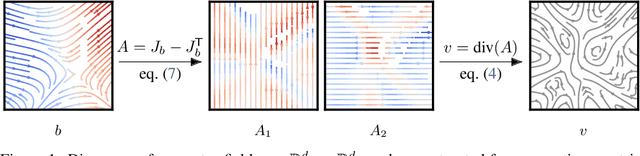
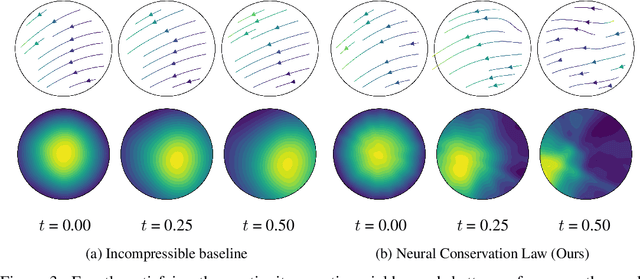
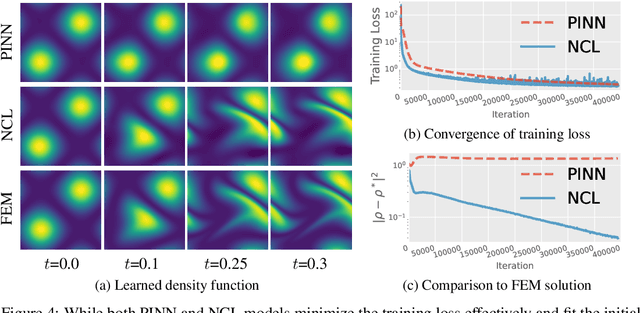
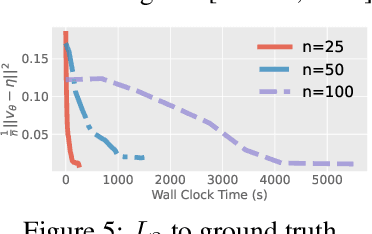
Abstract:We investigate the parameterization of deep neural networks that by design satisfy the continuity equation, a fundamental conservation law. This is enabled by the observation that solutions of the continuity equation can be represented as a divergence-free vector field. We hence propose building divergence-free neural networks through the concept of differential forms, and with the aid of automatic differentiation, realize two practical constructions. As a result, we can parameterize pairs of densities and vector fields that always satisfy the continuity equation by construction, foregoing the need for extra penalty methods or expensive numerical simulation. Furthermore, we prove these models are universal and so can be used to represent any divergence-free vector field. Finally, we experimentally validate our approaches on neural network-based solutions to fluid equations, solving for the Hodge decomposition, and learning dynamical optimal transport maps the Hodge decomposition, and learning dynamical optimal transport maps.
Latent State Marginalization as a Low-cost Approach for Improving Exploration
Oct 03, 2022

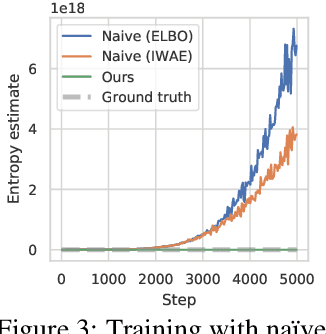
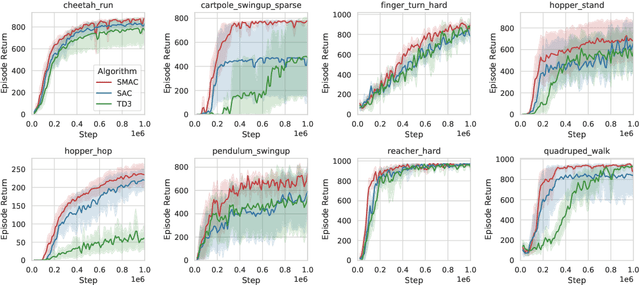
Abstract:While the maximum entropy (MaxEnt) reinforcement learning (RL) framework -- often touted for its exploration and robustness capabilities -- is usually motivated from a probabilistic perspective, the use of deep probabilistic models has not gained much traction in practice due to their inherent complexity. In this work, we propose the adoption of latent variable policies within the MaxEnt framework, which we show can provably approximate any policy distribution, and additionally, naturally emerges under the use of world models with a latent belief state. We discuss why latent variable policies are difficult to train, how naive approaches can fail, then subsequently introduce a series of improvements centered around low-cost marginalization of the latent state, allowing us to make full use of the latent state at minimal additional cost. We instantiate our method under the actor-critic framework, marginalizing both the actor and critic. The resulting algorithm, referred to as Stochastic Marginal Actor-Critic (SMAC), is simple yet effective. We experimentally validate our method on continuous control tasks, showing that effective marginalization can lead to better exploration and more robust training.
Unifying Generative Models with GFlowNets
Sep 06, 2022Abstract:There are many frameworks for deep generative modeling, each often presented with their own specific training algorithms and inference methods. We present a short note on the connections between existing deep generative models and the GFlowNet framework, shedding light on their overlapping traits and providing a unifying viewpoint through the lens of learning with Markovian trajectories. This provides a means for unifying training and inference algorithms, and provides a route to construct an agglomeration of generative models.
Matching Normalizing Flows and Probability Paths on Manifolds
Jul 11, 2022
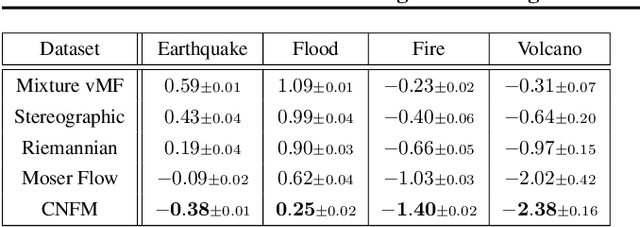
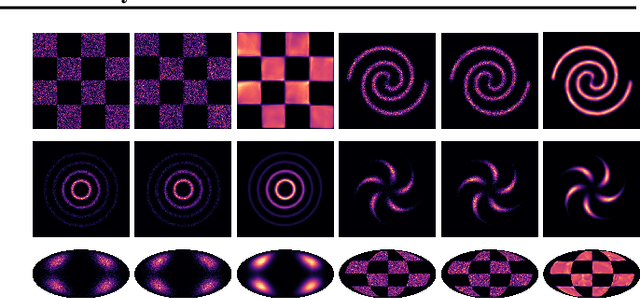
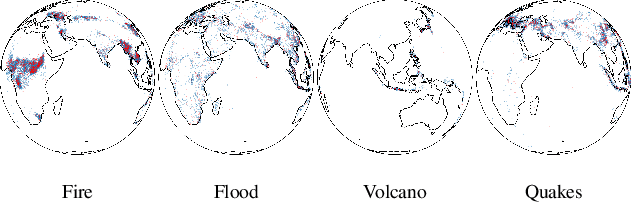
Abstract:Continuous Normalizing Flows (CNFs) are a class of generative models that transform a prior distribution to a model distribution by solving an ordinary differential equation (ODE). We propose to train CNFs on manifolds by minimizing probability path divergence (PPD), a novel family of divergences between the probability density path generated by the CNF and a target probability density path. PPD is formulated using a logarithmic mass conservation formula which is a linear first order partial differential equation relating the log target probabilities and the CNF's defining vector field. PPD has several key benefits over existing methods: it sidesteps the need to solve an ODE per iteration, readily applies to manifold data, scales to high dimensions, and is compatible with a large family of target paths interpolating pure noise and data in finite time. Theoretically, PPD is shown to bound classical probability divergences. Empirically, we show that CNFs learned by minimizing PPD achieve state-of-the-art results in likelihoods and sample quality on existing low-dimensional manifold benchmarks, and is the first example of a generative model to scale to moderately high dimensional manifolds.
Semi-Discrete Normalizing Flows through Differentiable Tessellation
Mar 14, 2022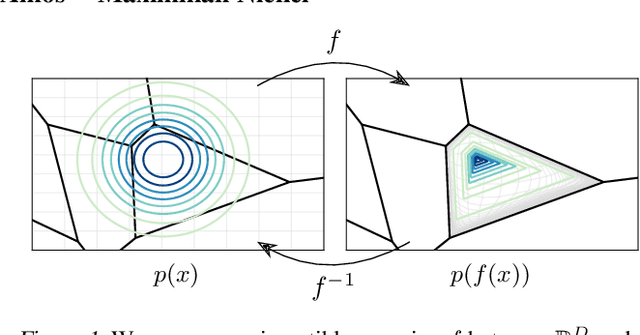
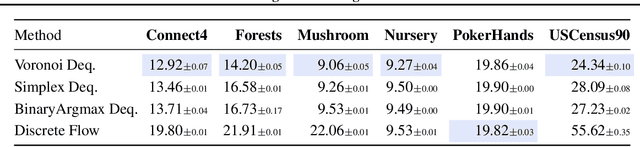
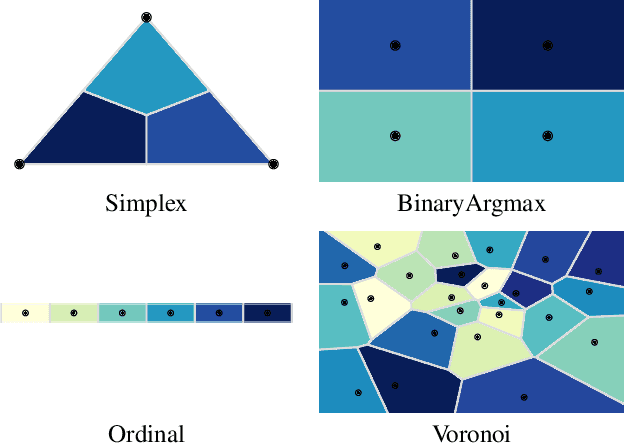

Abstract:Mapping between discrete and continuous distributions is a difficult task and many have had to resort to approximate or heuristical approaches. We propose a tessellation-based approach that directly learns quantization boundaries on a continuous space, complete with exact likelihood evaluations. This is done through constructing normalizing flows on convex polytopes parameterized through a differentiable Voronoi tessellation. Using a simple homeomorphism with an efficient log determinant Jacobian, we can then cheaply parameterize distributions on convex polytopes. We explore this approach in two application settings, mapping from discrete to continuous and vice versa. Firstly, a Voronoi dequantization allows automatically learning quantization boundaries in a multidimensional space. The location of boundaries and distances between regions can encode useful structural relations between the quantized discrete values. Secondly, a Voronoi mixture model has constant computation cost for likelihood evaluation regardless of the number of mixture components. Empirically, we show improvements over existing methods across a range of structured data modalities, and find that we can achieve a significant gain from just adding Voronoi mixtures to a baseline model.
Infinitely Deep Bayesian Neural Networks with Stochastic Differential Equations
Feb 12, 2021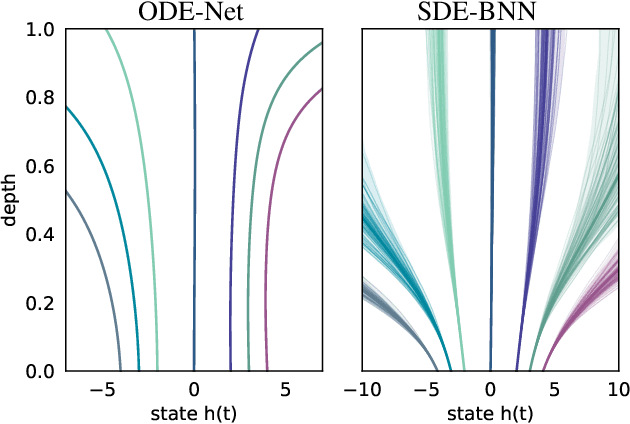
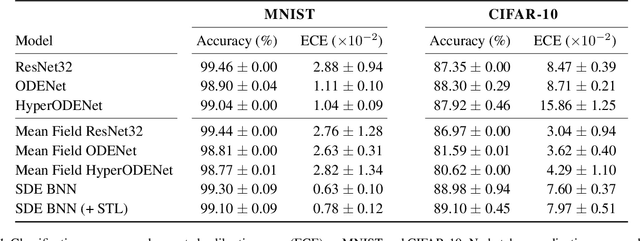
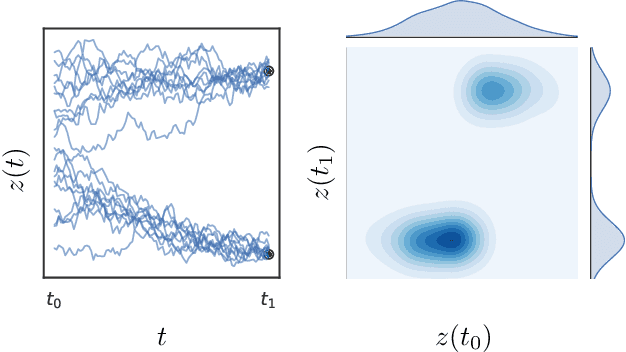
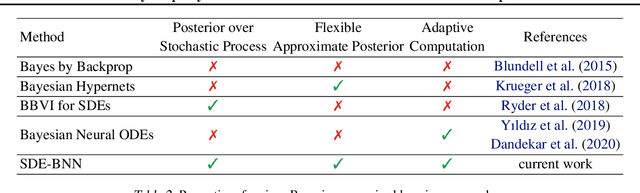
Abstract:We perform scalable approximate inference in a recently-proposed family of continuous-depth Bayesian neural networks. In this model class, uncertainty about separate weights in each layer produces dynamics that follow a stochastic differential equation (SDE). We demonstrate gradient-based stochastic variational inference in this infinite-parameter setting, producing arbitrarily-flexible approximate posteriors. We also derive a novel gradient estimator that approaches zero variance as the approximate posterior approaches the true posterior. This approach further inherits the memory-efficient training and tunable precision of neural ODEs.
Convex Potential Flows: Universal Probability Distributions with Optimal Transport and Convex Optimization
Dec 10, 2020
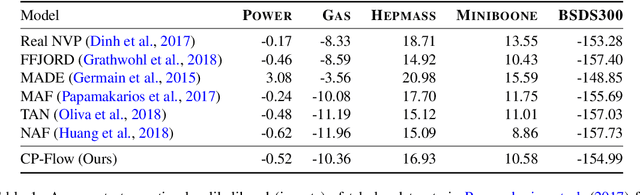
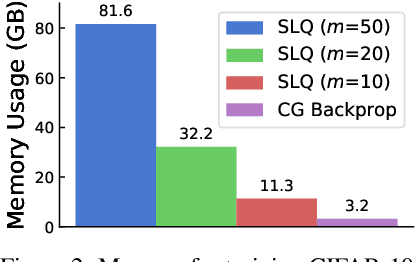
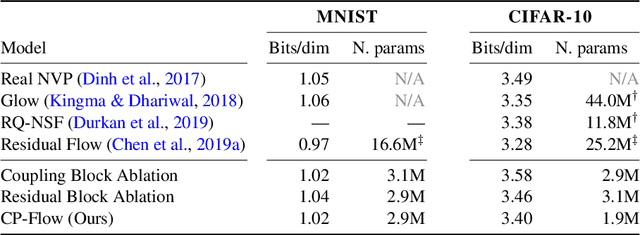
Abstract:Flow-based models are powerful tools for designing probabilistic models with tractable density. This paper introduces Convex Potential Flows (CP-Flow), a natural and efficient parameterization of invertible models inspired by the optimal transport (OT) theory. CP-Flows are the gradient map of a strongly convex neural potential function. The convexity implies invertibility and allows us to resort to convex optimization to solve the convex conjugate for efficient inversion. To enable maximum likelihood training, we derive a new gradient estimator of the log-determinant of the Jacobian, which involves solving an inverse-Hessian vector product using the conjugate gradient method. The gradient estimator has constant-memory cost, and can be made effectively unbiased by reducing the error tolerance level of the convex optimization routine. Theoretically, we prove that CP-Flows are universal density approximators and are optimal in the OT sense. Our empirical results show that CP-Flow performs competitively on standard benchmarks of density estimation and variational inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge