Batch Normalization Explained

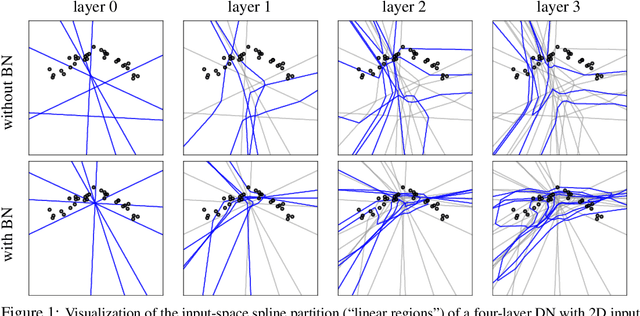
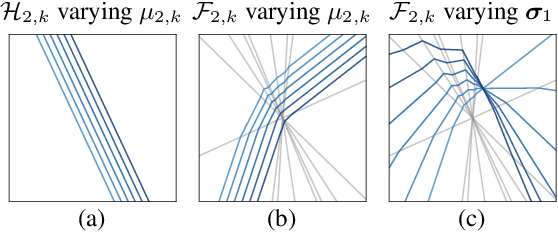
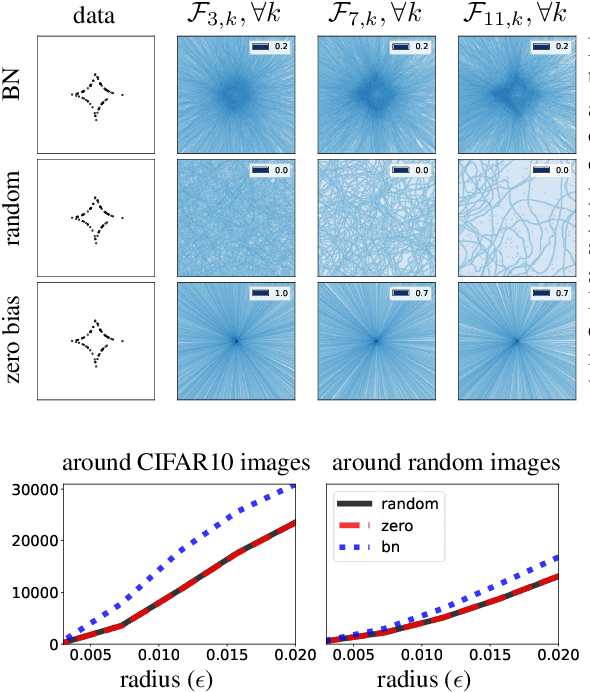
A critically important, ubiquitous, and yet poorly understood ingredient in modern deep networks (DNs) is batch normalization (BN), which centers and normalizes the feature maps. To date, only limited progress has been made understanding why BN boosts DN learning and inference performance; work has focused exclusively on showing that BN smooths a DN's loss landscape. In this paper, we study BN theoretically from the perspective of function approximation; we exploit the fact that most of today's state-of-the-art DNs are continuous piecewise affine (CPA) splines that fit a predictor to the training data via affine mappings defined over a partition of the input space (the so-called "linear regions"). {\em We demonstrate that BN is an unsupervised learning technique that -- independent of the DN's weights or gradient-based learning -- adapts the geometry of a DN's spline partition to match the data.} BN provides a "smart initialization" that boosts the performance of DN learning, because it adapts even a DN initialized with random weights to align its spline partition with the data. We also show that the variation of BN statistics between mini-batches introduces a dropout-like random perturbation to the partition boundaries and hence the decision boundary for classification problems. This per mini-batch perturbation reduces overfitting and improves generalization by increasing the margin between the training samples and the decision boundary.

Momentum Transformer: Closing the Performance Gap Between Self-attention and Its Linearization

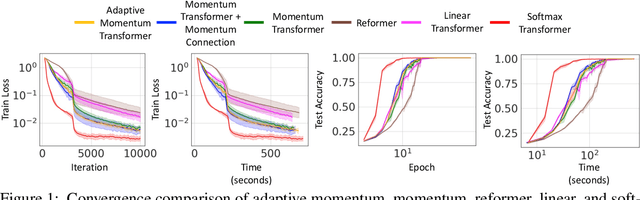
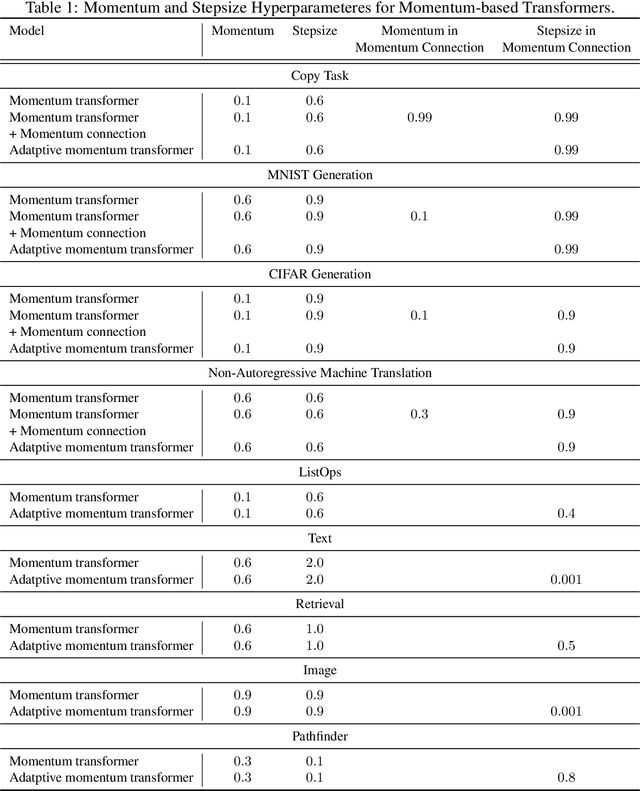
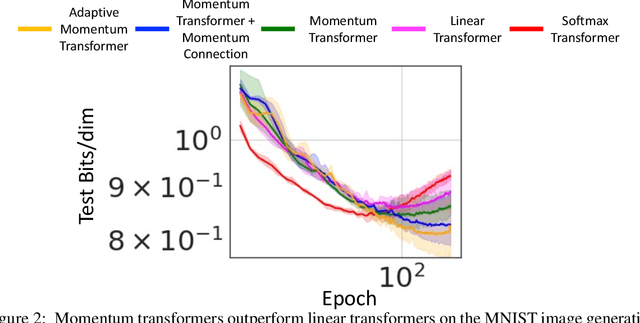
Transformers have achieved remarkable success in sequence modeling and beyond but suffer from quadratic computational and memory complexities with respect to the length of the input sequence. Leveraging techniques include sparse and linear attention and hashing tricks; efficient transformers have been proposed to reduce the quadratic complexity of transformers but significantly degrade the accuracy. In response, we first interpret the linear attention and residual connections in computing the attention map as gradient descent steps. We then introduce momentum into these components and propose the \emph{momentum transformer}, which utilizes momentum to improve the accuracy of linear transformers while maintaining linear memory and computational complexities. Furthermore, we develop an adaptive strategy to compute the momentum value for our model based on the optimal momentum for quadratic optimization. This adaptive momentum eliminates the need to search for the optimal momentum value and further enhances the performance of the momentum transformer. A range of experiments on both autoregressive and non-autoregressive tasks, including image generation and machine translation, demonstrate that the momentum transformer outperforms popular linear transformers in training efficiency and accuracy.

Benign Overparameterization in Membership Inference with Early Stopping

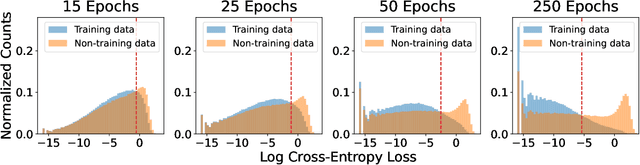
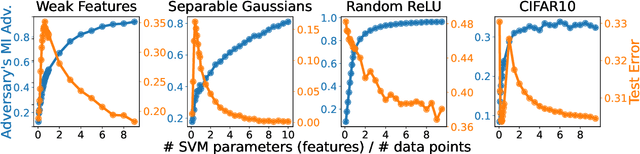
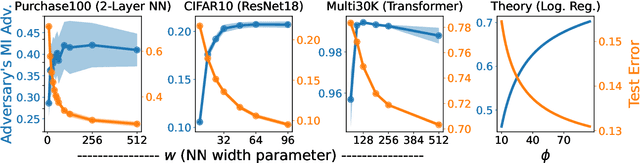
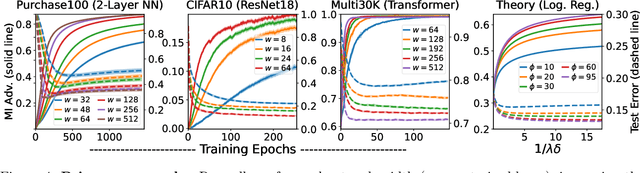
Does a neural network's privacy have to be at odds with its accuracy? In this work, we study the effects the number of training epochs and parameters have on a neural network's vulnerability to membership inference (MI) attacks, which aim to extract potentially private information about the training data. We first demonstrate how the number of training epochs and parameters individually induce a privacy-utility trade-off: more of either improves generalization performance at the expense of lower privacy. However, remarkably, we also show that jointly tuning both can eliminate this privacy-utility trade-off. Specifically, with careful tuning of the number of training epochs, more overparameterization can increase model privacy for fixed generalization error. To better understand these phenomena theoretically, we develop a powerful new leave-one-out analysis tool to study the asymptotic behavior of linear classifiers and apply it to characterize the sample-specific loss threshold MI attack in high-dimensional logistic regression. For practitioners, we introduce a low-overhead procedure to estimate MI risk and tune the number of training epochs to guard against MI attacks.

DeepTensor: Low-Rank Tensor Decomposition with Deep Network Priors

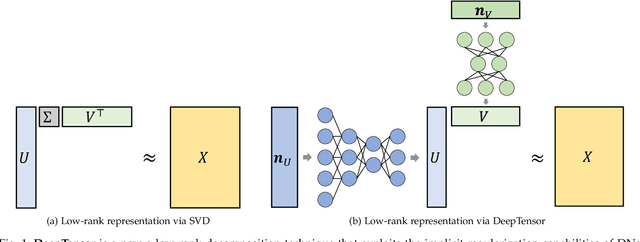
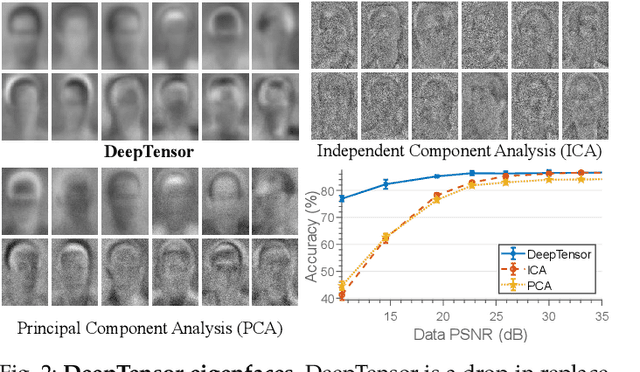
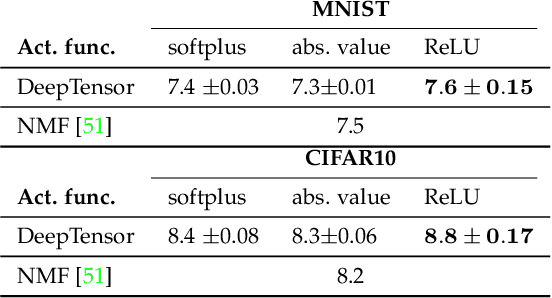
DeepTensor is a computationally efficient framework for low-rank decomposition of matrices and tensors using deep generative networks. We decompose a tensor as the product of low-rank tensor factors (e.g., a matrix as the outer product of two vectors), where each low-rank tensor is generated by a deep network (DN) that is trained in a self-supervised manner to minimize the mean-squared approximation error. Our key observation is that the implicit regularization inherent in DNs enables them to capture nonlinear signal structures (e.g., manifolds) that are out of the reach of classical linear methods like the singular value decomposition (SVD) and principal component analysis (PCA). Furthermore, in contrast to the SVD and PCA, whose performance deteriorates when the tensor's entries deviate from additive white Gaussian noise, we demonstrate that the performance of DeepTensor is robust to a wide range of distributions. We validate that DeepTensor is a robust and computationally efficient drop-in replacement for the SVD, PCA, nonnegative matrix factorization (NMF), and similar decompositions by exploring a range of real-world applications, including hyperspectral image denoising, 3D MRI tomography, and image classification. In particular, DeepTensor offers a 6dB signal-to-noise ratio improvement over standard denoising methods for signals corrupted by Poisson noise and learns to decompose 3D tensors 60 times faster than a single DN equipped with 3D convolutions.

Singular Value Perturbation and Deep Network Optimization

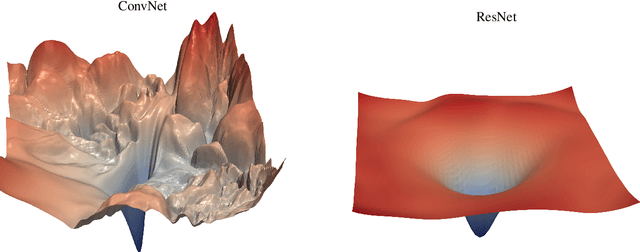
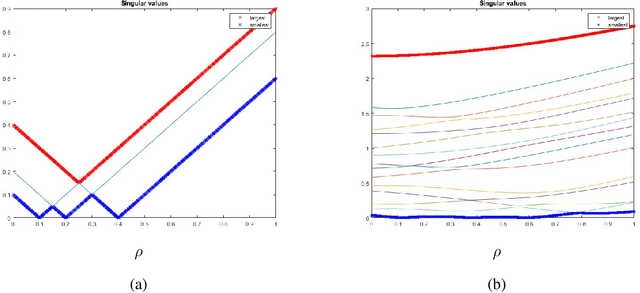
We develop new theoretical results on matrix perturbation to shed light on the impact of architecture on the performance of a deep network. In particular, we explain analytically what deep learning practitioners have long observed empirically: the parameters of some deep architectures (e.g., residual networks, ResNets, and Dense networks, DenseNets) are easier to optimize than others (e.g., convolutional networks, ConvNets). Building on our earlier work connecting deep networks with continuous piecewise-affine splines, we develop an exact local linear representation of a deep network layer for a family of modern deep networks that includes ConvNets at one end of a spectrum and ResNets, DenseNets, and other networks with skip connections at the other. For regression and classification tasks that optimize the squared-error loss, we show that the optimization loss surface of a modern deep network is piecewise quadratic in the parameters, with local shape governed by the singular values of a matrix that is a function of the local linear representation. We develop new perturbation results for how the singular values of matrices of this sort behave as we add a fraction of the identity and multiply by certain diagonal matrices. A direct application of our perturbation results explains analytically why a network with skip connections (such as a ResNet or DenseNet) is easier to optimize than a ConvNet: thanks to its more stable singular values and smaller condition number, the local loss surface of such a network is less erratic, less eccentric, and features local minima that are more accommodating to gradient-based optimization. Our results also shed new light on the impact of different nonlinear activation functions on a deep network's singular values, regardless of its architecture.

NeuroView-RNN: It's About Time

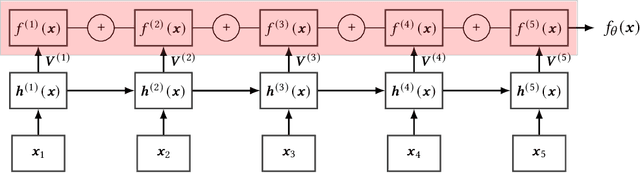
Recurrent Neural Networks (RNNs) are important tools for processing sequential data such as time-series or video. Interpretability is defined as the ability to be understood by a person and is different from explainability, which is the ability to be explained in a mathematical formulation. A key interpretability issue with RNNs is that it is not clear how each hidden state per time step contributes to the decision-making process in a quantitative manner. We propose NeuroView-RNN as a family of new RNN architectures that explains how all the time steps are used for the decision-making process. Each member of the family is derived from a standard RNN architecture by concatenation of the hidden steps into a global linear classifier. The global linear classifier has all the hidden states as the input, so the weights of the classifier have a linear mapping to the hidden states. Hence, from the weights, NeuroView-RNN can quantify how important each time step is to a particular decision. As a bonus, NeuroView-RNN also offers higher accuracy in many cases compared to the RNNs and their variants. We showcase the benefits of NeuroView-RNN by evaluating on a multitude of diverse time-series datasets.

On Local Distributions in Graph Signal Processing

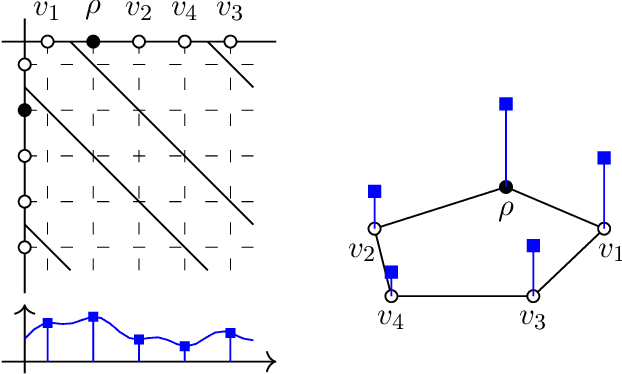
Graph filtering is the cornerstone operation in graph signal processing (GSP). Thus, understanding it is key in developing potent GSP methods. Graph filters are local and distributed linear operations, whose output depends only on the local neighborhood of each node. Moreover, a graph filter's output can be computed separately at each node by carrying out repeated exchanges with immediate neighbors. Graph filters can be compactly written as polynomials of a graph shift operator (typically, a sparse matrix description of the graph). This has led to relating the properties of the filters with the spectral properties of the corresponding matrix -- which encodes global structure of the graph. In this work, we propose a framework that relies solely on the local distribution of the neighborhoods of a graph. The crux of this approach is to describe graphs and graph signals in terms of a measurable space of rooted balls. Leveraging this, we are able to seamlessly compare graphs of different sizes and coming from different models, yielding results on the convergence of spectral densities, transferability of filters across arbitrary graphs, and continuity of graph signal properties with respect to the distribution of local substructures.

Open-Ended Knowledge Tracing

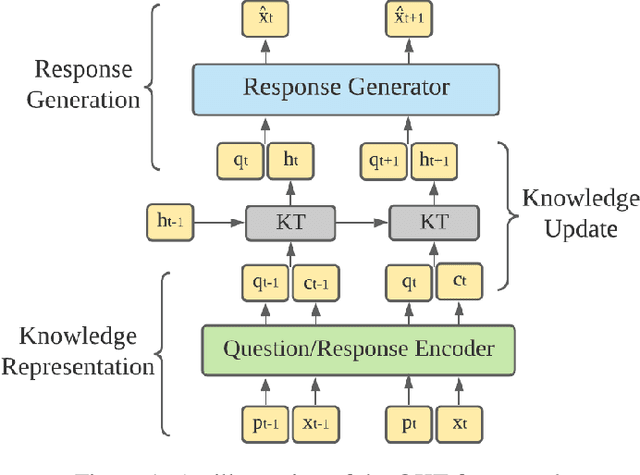
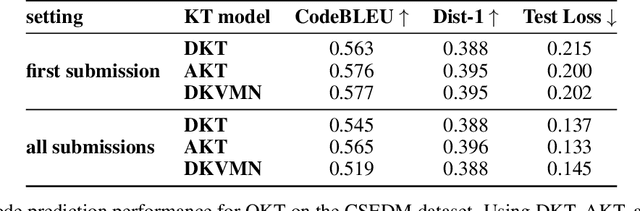
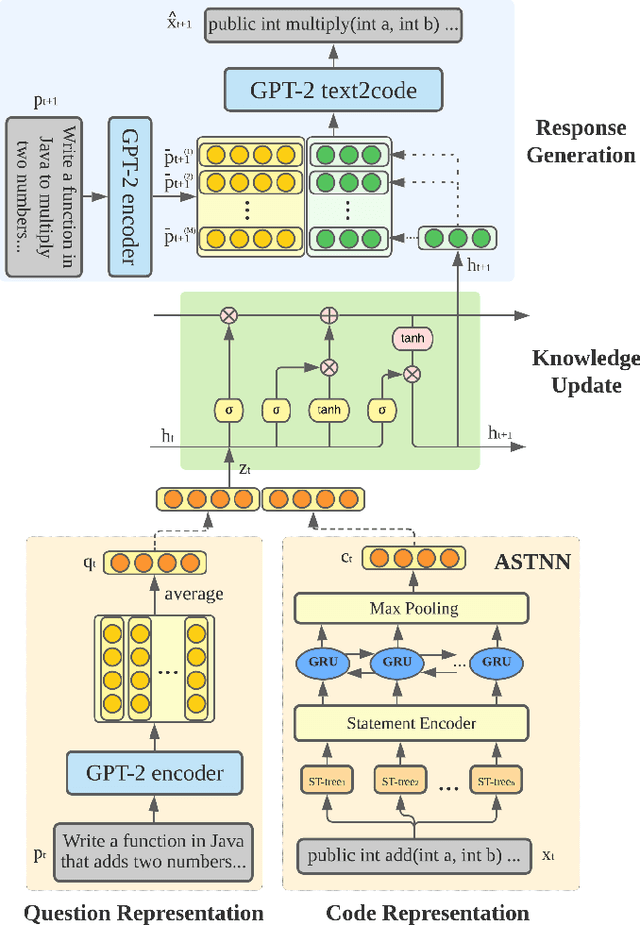
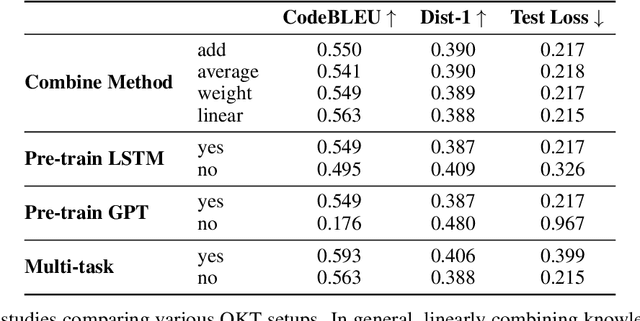
Knowledge tracing refers to the problem of estimating each student's knowledge component/skill mastery level from their past responses to questions in educational applications. One direct benefit knowledge tracing methods provide is the ability to predict each student's performance on the future questions. However, one key limitation of most existing knowledge tracing methods is that they treat student responses to questions as binary-valued, i.e., whether the responses are correct or incorrect. Response correctness analysis/prediction is easy to navigate but loses important information, especially for open-ended questions: the exact student responses can potentially provide much more information about their knowledge states than only response correctness. In this paper, we present our first exploration into open-ended knowledge tracing, i.e., the analysis and prediction of students' open-ended responses to questions in the knowledge tracing setup. We first lay out a generic framework for open-ended knowledge tracing before detailing its application to the domain of computer science education with programming questions. We define a series of evaluation metrics in this domain and conduct a series of quantitative and qualitative experiments to test the boundaries of open-ended knowledge tracing methods on a real-world student code dataset.

MINER: Multiscale Implicit Neural Representations

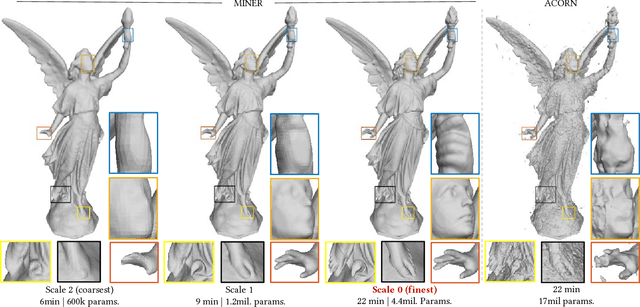
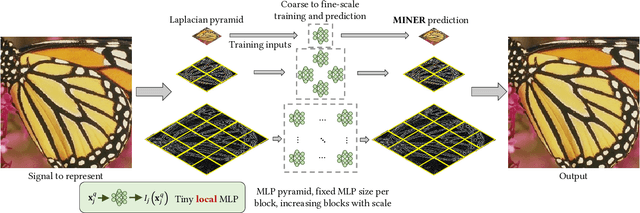
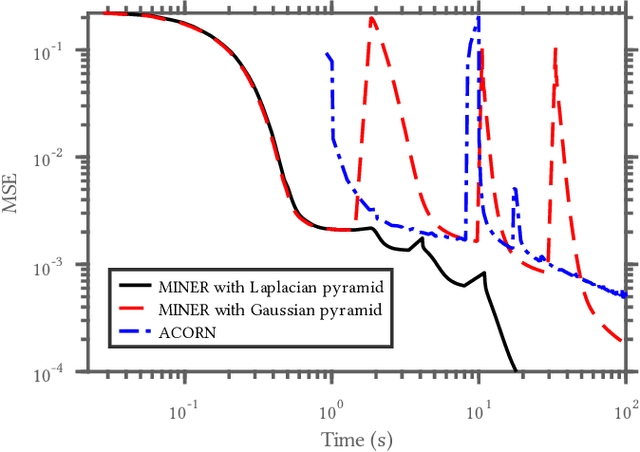
We introduce a new neural signal representation designed for the efficient high-resolution representation of large-scale signals. The key innovation in our multiscale implicit neural representation (MINER) is an internal representation via a Laplacian pyramid, which provides a sparse multiscale representation of the signal that captures orthogonal parts of the signal across scales. We leverage the advantages of the Laplacian pyramid by representing small disjoint patches of the pyramid at each scale with a tiny MLP. This enables the capacity of the network to adaptively increase from coarse to fine scales, and only represent parts of the signal with strong signal energy. The parameters of each MLP are optimized from coarse-to-fine scale which results in faster approximations at coarser scales, thereby ultimately an extremely fast training process. We apply MINER to a range of large-scale signal representation tasks, including gigapixel images and very large point clouds, and demonstrate that it requires fewer than 25% of the parameters, 33% of the memory footprint, and 10% of the computation time of competing techniques such as ACORN to reach the same representation error.

Parameters or Privacy: A Provable Tradeoff Between Overparameterization and Membership Inference

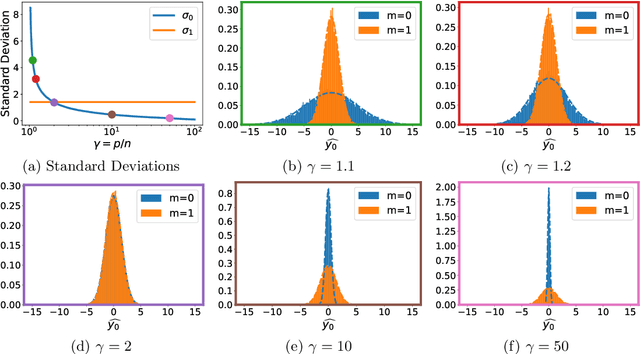
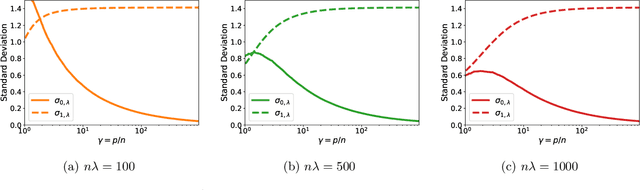
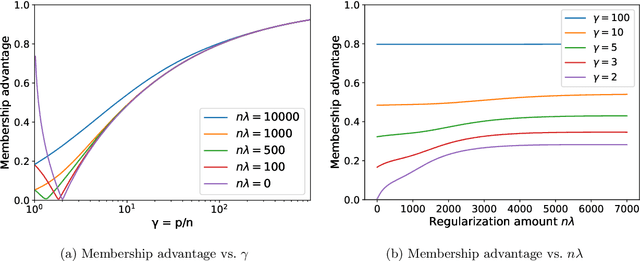
A surprising phenomenon in modern machine learning is the ability of a highly overparameterized model to generalize well (small error on the test data) even when it is trained to memorize the training data (zero error on the training data). This has led to an arms race towards increasingly overparameterized models (c.f., deep learning). In this paper, we study an underexplored hidden cost of overparameterization: the fact that overparameterized models are more vulnerable to privacy attacks, in particular the membership inference attack that predicts the (potentially sensitive) examples used to train a model. We significantly extend the relatively few empirical results on this problem by theoretically proving for an overparameterized linear regression model with Gaussian data that the membership inference vulnerability increases with the number of parameters. Moreover, a range of empirical studies indicates that more complex, nonlinear models exhibit the same behavior. Finally, we study different methods for mitigating such attacks in the overparameterized regime, such as noise addition and regularization, and conclude that simply reducing the parameters of an overparameterized model is an effective strategy to protect it from membership inference without greatly decreasing its generalization error.