On Local Distributions in Graph Signal Processing

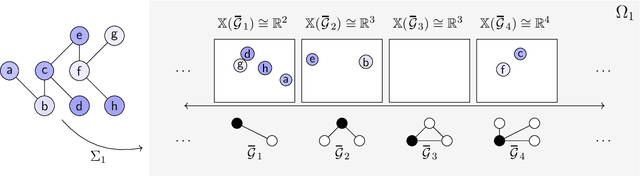
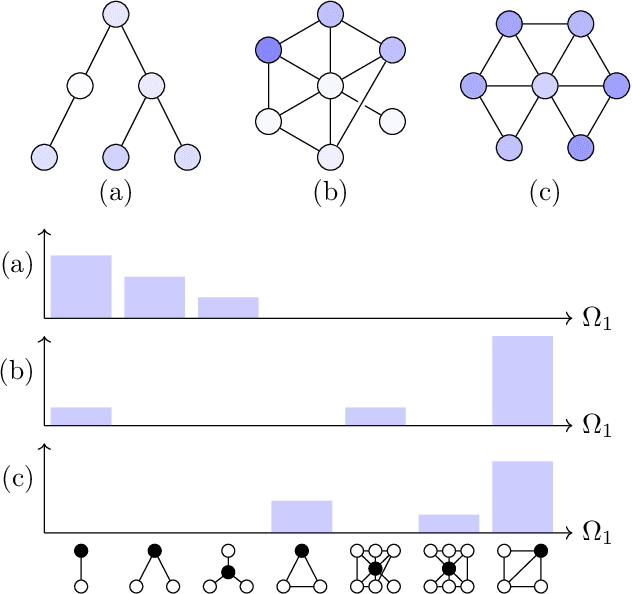
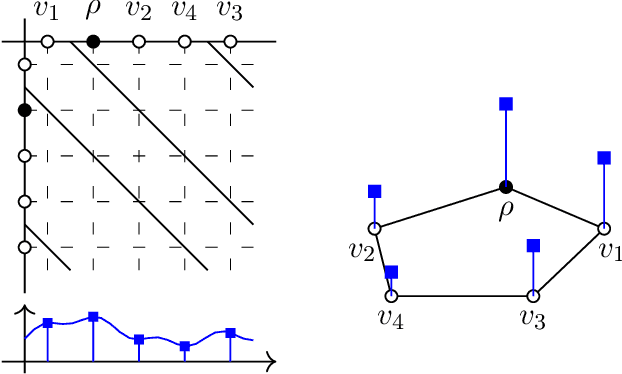
Graph filtering is the cornerstone operation in graph signal processing (GSP). Thus, understanding it is key in developing potent GSP methods. Graph filters are local and distributed linear operations, whose output depends only on the local neighborhood of each node. Moreover, a graph filter's output can be computed separately at each node by carrying out repeated exchanges with immediate neighbors. Graph filters can be compactly written as polynomials of a graph shift operator (typically, a sparse matrix description of the graph). This has led to relating the properties of the filters with the spectral properties of the corresponding matrix -- which encodes global structure of the graph. In this work, we propose a framework that relies solely on the local distribution of the neighborhoods of a graph. The crux of this approach is to describe graphs and graph signals in terms of a measurable space of rooted balls. Leveraging this, we are able to seamlessly compare graphs of different sizes and coming from different models, yielding results on the convergence of spectral densities, transferability of filters across arbitrary graphs, and continuity of graph signal properties with respect to the distribution of local substructures.