Implicit Neural Representations and the Algebra of Complex Wavelets

Implicit neural representations (INRs) have arisen as useful methods for representing signals on Euclidean domains. By parameterizing an image as a multilayer perceptron (MLP) on Euclidean space, INRs effectively represent signals in a way that couples spatial and spectral features of the signal that is not obvious in the usual discrete representation, paving the way for continuous signal processing and machine learning approaches that were not previously possible. Although INRs using sinusoidal activation functions have been studied in terms of Fourier theory, recent works have shown the advantage of using wavelets instead of sinusoids as activation functions, due to their ability to simultaneously localize in both frequency and space. In this work, we approach such INRs and demonstrate how they resolve high-frequency features of signals from coarse approximations done in the first layer of the MLP. This leads to multiple prescriptions for the design of INR architectures, including the use of complex wavelets, decoupling of low and band-pass approximations, and initialization schemes based on the singularities of the desired signal.

Signal Processing on Product Spaces

We establish a framework for signal processing on product spaces of simplicial and cellular complexes. For simplicity, we focus on the product of two complexes representing time and space, although our results generalize naturally to products of simplicial complexes of arbitrary dimension. Our framework leverages the structure of the eigenmodes of the Hodge Laplacian of the product space to jointly filter along time and space. To this end, we provide a decomposition theorem of the Hodge Laplacian of the product space, which highlights how the product structure induces a decomposition of each eigenmode into a spatial and temporal component. Finally, we apply our method to real world data, specifically for interpolating trajectories of buoys in the ocean from a limited set of observed trajectories.

Windowed Fourier Analysis for Signal Processing on Graph Bundles

We consider the task of representing signals supported on graph bundles, which are generalizations of product graphs that allow for "twists" in the product structure. Leveraging the localized product structure of a graph bundle, we demonstrate how a suitable partition of unity over the base graph can be used to lift the signal on the graph into a space where a product factorization can be readily applied. Motivated by the locality of this procedure, we demonstrate that bases for the signal spaces of the components of the graph bundle can be lifted in the same way, yielding a basis for the signal space of the total graph. We demonstrate this construction on synthetic graphs, as well as with an analysis of the energy landscape of conformational manifolds in stereochemistry.

Enhanced graph-learning schemes driven by similar distributions of motifs

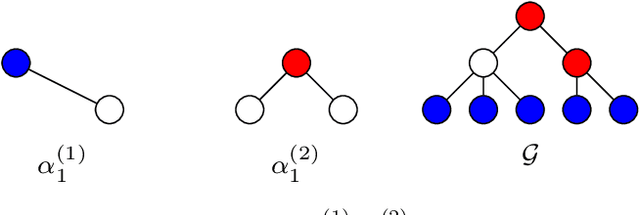
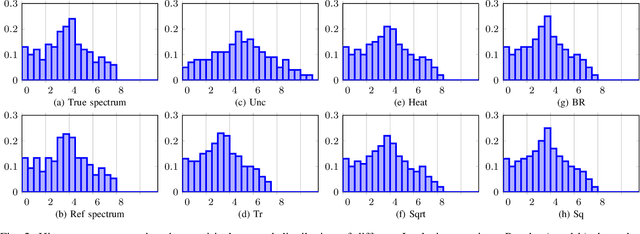
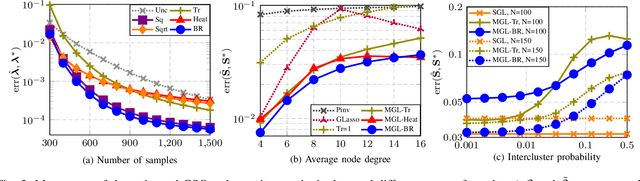
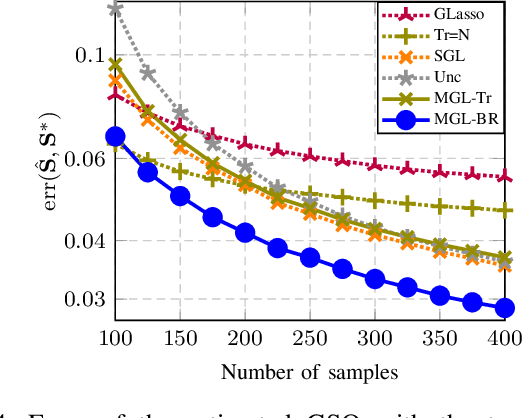
This paper looks at the task of network topology inference, where the goal is to learn an unknown graph from nodal observations. One of the novelties of the approach put forth is the consideration of prior information about the density of motifs of the unknown graph to enhance the inference of classical Gaussian graphical models. Dealing with the density of motifs directly constitutes a challenging combinatorial task. However, we note that if two graphs have similar motif densities, one can show that the expected value of a polynomial applied to their empirical spectral distributions will be similar. Guided by this, we first assume that we have a reference graph that is related to the sought graph (in the sense of having similar motif densities) and then, we exploit this relation by incorporating a similarity constraint and a regularization term in the network topology inference optimization problem. The (non-)convexity of the optimization problem is discussed and a computational efficient alternating majorization-minimization algorithm is designed. We assess the performance of the proposed method through exhaustive numerical experiments where different constraints are considered and compared against popular baselines algorithms on both synthetic and real-world datasets.

On Local Distributions in Graph Signal Processing

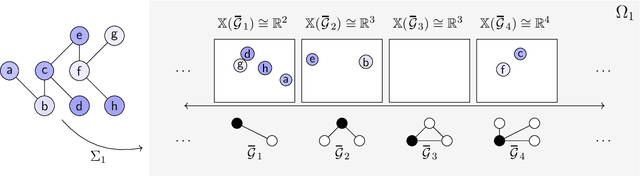
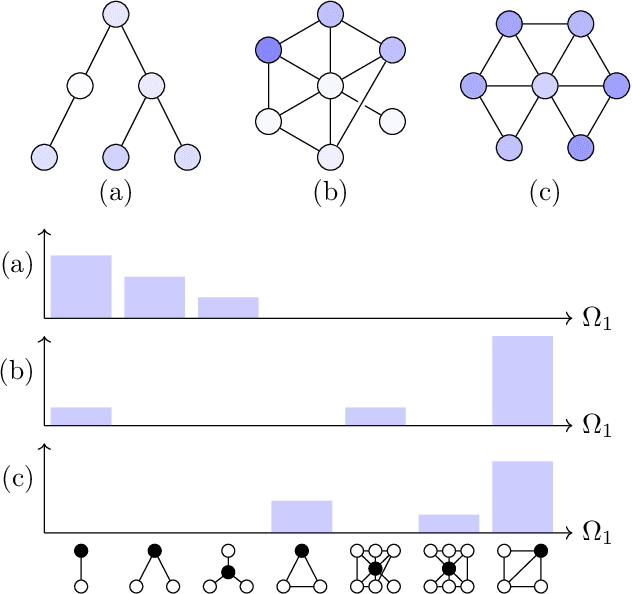
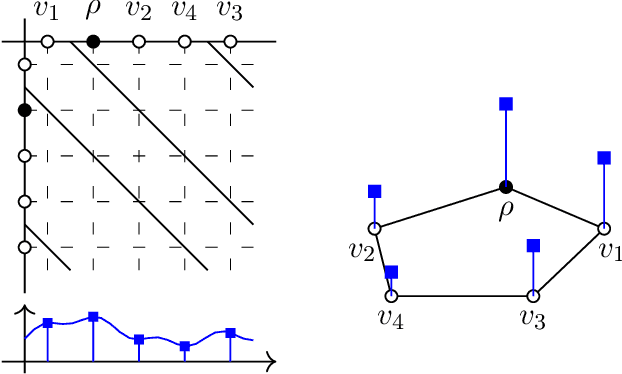
Graph filtering is the cornerstone operation in graph signal processing (GSP). Thus, understanding it is key in developing potent GSP methods. Graph filters are local and distributed linear operations, whose output depends only on the local neighborhood of each node. Moreover, a graph filter's output can be computed separately at each node by carrying out repeated exchanges with immediate neighbors. Graph filters can be compactly written as polynomials of a graph shift operator (typically, a sparse matrix description of the graph). This has led to relating the properties of the filters with the spectral properties of the corresponding matrix -- which encodes global structure of the graph. In this work, we propose a framework that relies solely on the local distribution of the neighborhoods of a graph. The crux of this approach is to describe graphs and graph signals in terms of a measurable space of rooted balls. Leveraging this, we are able to seamlessly compare graphs of different sizes and coming from different models, yielding results on the convergence of spectral densities, transferability of filters across arbitrary graphs, and continuity of graph signal properties with respect to the distribution of local substructures.

Signal Processing on Cell Complexes

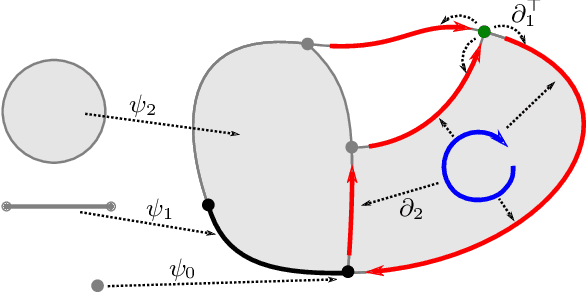
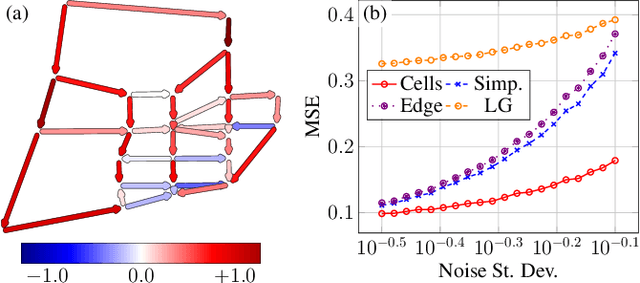
The processing of signals supported on non-Euclidean domains has attracted large interest in the last years. Thus far, such non-Euclidean domains have been abstracted primarily as graphs with signals supported on the nodes, though recently the processing of signals on more general structures such as simplicial complexes has also been considered. In this paper, we give an introduction to signal processing on (abstract) regular cell complexes, which provide a unifying framework encompassing graphs, simplicial complexes, cubical complexes and various meshes as special cases. We discuss how appropriate Hodge Laplacians for these cell complexes can be derived. These Hodge Laplacians enable the construction of convolutional filters, which can be employed in linear filtering and non-linear filtering via neural networks defined on cell complexes.

Hodgelets: Localized Spectral Representations of Flows on Simplicial Complexes

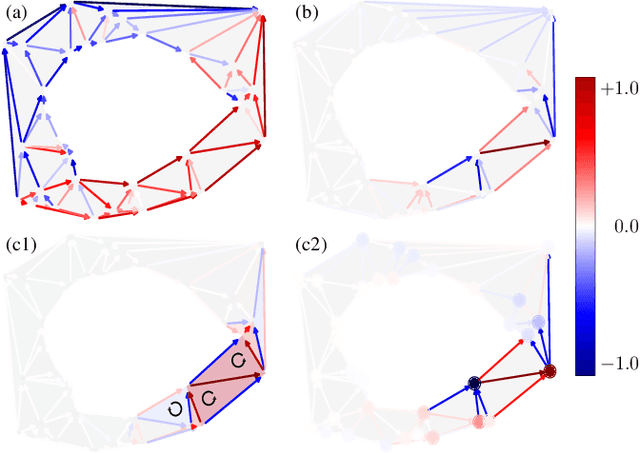
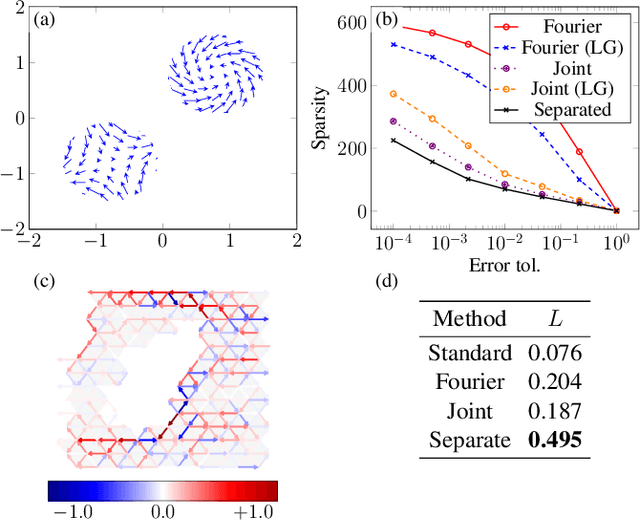
We develop wavelet representations for edge-flows on simplicial complexes, using ideas rooted in combinatorial Hodge theory and spectral graph wavelets. We first show that the Hodge Laplacian can be used in lieu of the graph Laplacian to construct a family of wavelets for higher-order signals on simplicial complexes. Then, we refine this idea to construct wavelets that respect the Hodge-Helmholtz decomposition. For these Hodgelets, familiar notions of curl-free and divergence-free flows from vector calculus are preserved. We characterize the representational quality of our Hodgelets for edge flows in terms of frame bounds and demonstrate the use of these spectral wavelets for sparse representation of edge flows on real and synthetic data.

Signal processing on simplicial complexes

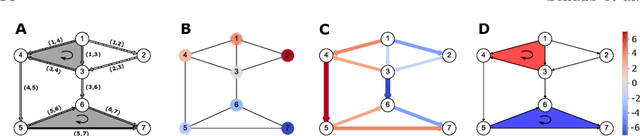
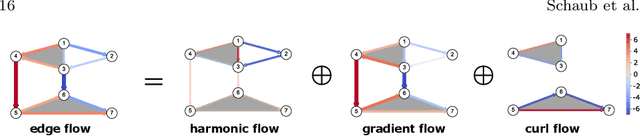
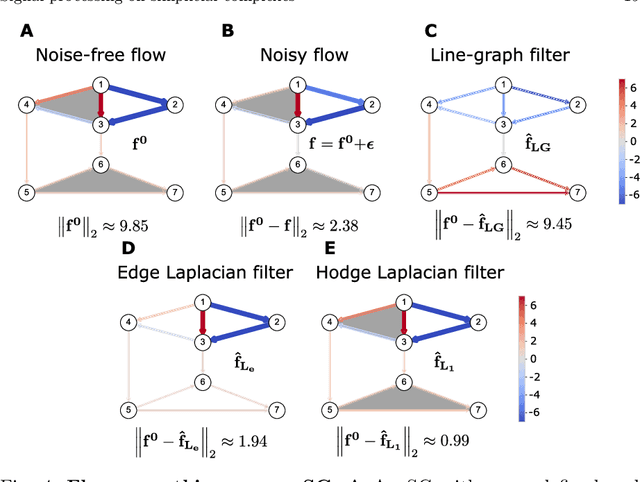
Higher-order networks have so far been considered primarily in the context of studying the structure of complex systems, i.e., the higher-order or multi-way relations connecting the constituent entities. More recently, a number of studies have considered dynamical processes that explicitly account for such higher-order dependencies, e.g., in the context of epidemic spreading processes or opinion formation. In this chapter, we focus on a closely related, but distinct third perspective: how can we use higher-order relationships to process signals and data supported on higher-order network structures. In particular, we survey how ideas from signal processing of data supported on regular domains, such as time series or images, can be extended to graphs and simplicial complexes. We discuss Fourier analysis, signal denoising, signal interpolation, and nonlinear processing through neural networks based on simplicial complexes. Key to our developments is the Hodge Laplacian matrix, a multi-relational operator that leverages the special structure of simplicial complexes and generalizes desirable properties of the Laplacian matrix in graph signal processing.

An Impossibility Theorem for Node Embedding

With the increasing popularity of graph-based methods for dimensionality reduction and representation learning, node embedding functions have become important objects of study in the literature. In this paper, we take an axiomatic approach to understanding node embedding methods, first stating three properties for embedding dissimilarity networks, then proving that all three cannot be satisfied simultaneously by any node embedding method. Similar to existing results on the impossibility of clustering under certain axiomatic assumptions, this points to fundamental difficulties inherent to node embedding tasks. Once these difficulties are identified, we then relax these axioms to allow for certain node embedding methods to be admissible in our framework.

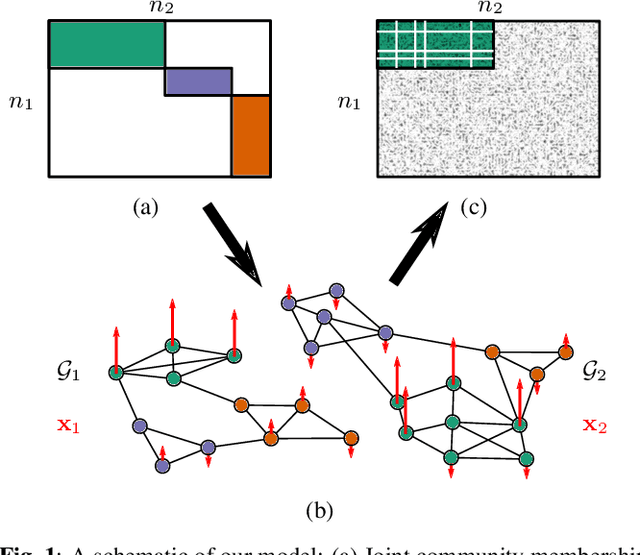
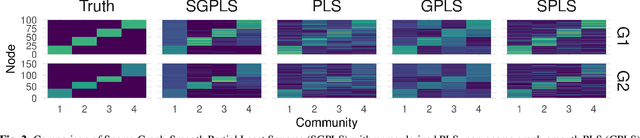
Sparse Partial Least Squares for Coarse Noisy Graph Alignment

Graph signal processing (GSP) provides a powerful framework for analyzing signals arising in a variety of domains. In many applications of GSP, multiple network structures are available, each of which captures different aspects of the same underlying phenomenon. To integrate these different data sources, graph alignment techniques attempt to find the best correspondence between vertices of two graphs. We consider a generalization of this problem, where there is no natural one-to-one mapping between vertices, but where there is correspondence between the community structures of each graph. Because we seek to learn structure at this higher community level, we refer to this problem as "coarse" graph alignment. To this end, we propose a novel regularized partial least squares method which both incorporates the observed graph structures and imposes sparsity in order to reflect the underlying block community structure. We provide efficient algorithms for our method and demonstrate its effectiveness in simulations.