Raul Astudillo
Bayesian preference elicitation for decision support in multiobjective optimization
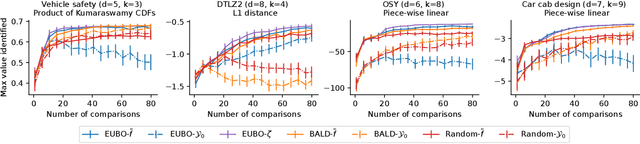
Jul 22, 2025Abstract:We present a novel approach to help decision-makers efficiently identify preferred solutions from the Pareto set of a multi-objective optimization problem. Our method uses a Bayesian model to estimate the decision-maker's utility function based on pairwise comparisons. Aided by this model, a principled elicitation strategy selects queries interactively to balance exploration and exploitation, guiding the discovery of high-utility solutions. The approach is flexible: it can be used interactively or a posteriori after estimating the Pareto front through standard multi-objective optimization techniques. Additionally, at the end of the elicitation phase, it generates a reduced menu of high-quality solutions, simplifying the decision-making process. Through experiments on test problems with up to nine objectives, our method demonstrates superior performance in finding high-utility solutions with a small number of queries. We also provide an open-source implementation of our method to support its adoption by the broader community.
Steering Generative Models with Experimental Data for Protein Fitness Optimization
May 21, 2025Abstract:Protein fitness optimization involves finding a protein sequence that maximizes desired quantitative properties in a combinatorially large design space of possible sequences. Recent developments in steering protein generative models (e.g diffusion models, language models) offer a promising approach. However, by and large, past studies have optimized surrogate rewards and/or utilized large amounts of labeled data for steering, making it unclear how well existing methods perform and compare to each other in real-world optimization campaigns where fitness is measured by low-throughput wet-lab assays. In this study, we explore fitness optimization using small amounts (hundreds) of labeled sequence-fitness pairs and comprehensively evaluate strategies such as classifier guidance and posterior sampling for guiding generation from different discrete diffusion models of protein sequences. We also demonstrate how guidance can be integrated into adaptive sequence selection akin to Thompson sampling in Bayesian optimization, showing that plug-and-play guidance strategies offer advantages compared to alternatives such as reinforcement learning with protein language models.
Practical Bayesian Algorithm Execution via Posterior Sampling
Oct 27, 2024Abstract:We consider Bayesian algorithm execution (BAX), a framework for efficiently selecting evaluation points of an expensive function to infer a property of interest encoded as the output of a base algorithm. Since the base algorithm typically requires more evaluations than are feasible, it cannot be directly applied. Instead, BAX methods sequentially select evaluation points using a probabilistic numerical approach. Current BAX methods use expected information gain to guide this selection. However, this approach is computationally intensive. Observing that, in many tasks, the property of interest corresponds to a target set of points defined by the function, we introduce PS-BAX, a simple, effective, and scalable BAX method based on posterior sampling. PS-BAX is applicable to a wide range of problems, including many optimization variants and level set estimation. Experiments across diverse tasks demonstrate that PS-BAX performs competitively with existing baselines while being significantly faster, simpler to implement, and easily parallelizable, setting a strong baseline for future research. Additionally, we establish conditions under which PS-BAX is asymptotically convergent, offering new insights into posterior sampling as an algorithm design paradigm.
Cost-aware Bayesian optimization via the Pandora's Box Gittins index
Jun 28, 2024



Abstract:Bayesian optimization is a technique for efficiently optimizing unknown functions in a black-box manner. To handle practical settings where gathering data requires use of finite resources, it is desirable to explicitly incorporate function evaluation costs into Bayesian optimization policies. To understand how to do so, we develop a previously-unexplored connection between cost-aware Bayesian optimization and the Pandora's Box problem, a decision problem from economics. The Pandora's Box problem admits a Bayesian-optimal solution based on an expression called the Gittins index, which can be reinterpreted as an acquisition function. We study the use of this acquisition function for cost-aware Bayesian optimization, and demonstrate empirically that it performs well, particularly in medium-high dimensions. We further show that this performance carries over to classical Bayesian optimization without explicit evaluation costs. Our work constitutes a first step towards integrating techniques from Gittins index theory into Bayesian optimization.
Preferential Multi-Objective Bayesian Optimization
Jun 20, 2024Abstract:Preferential Bayesian optimization (PBO) is a framework for optimizing a decision-maker's latent preferences over available design choices. While preferences often involve multiple conflicting objectives, existing work in PBO assumes that preferences can be encoded by a single objective function. For example, in robotic assistive devices, technicians often attempt to maximize user comfort while simultaneously minimizing mechanical energy consumption for longer battery life. Similarly, in autonomous driving policy design, decision-makers wish to understand the trade-offs between multiple safety and performance attributes before committing to a policy. To address this gap, we propose the first framework for PBO with multiple objectives. Within this framework, we present dueling scalarized Thompson sampling (DSTS), a multi-objective generalization of the popular dueling Thompson algorithm, which may be of interest beyond the PBO setting. We evaluate DSTS across four synthetic test functions and two simulated exoskeleton personalization and driving policy design tasks, showing that it outperforms several benchmarks. Finally, we prove that DSTS is asymptotically consistent. As a direct consequence, this result provides, to our knowledge, the first convergence guarantee for dueling Thompson sampling in the PBO setting.
Bayesian Optimization of Function Networks with Partial Evaluations
Nov 03, 2023



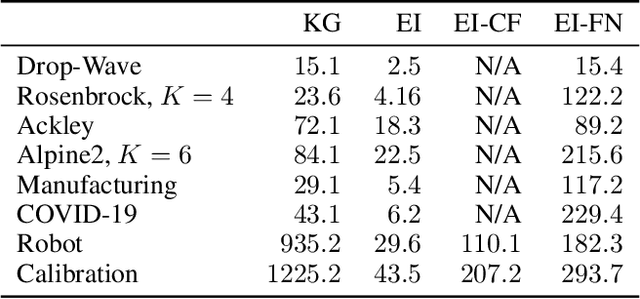
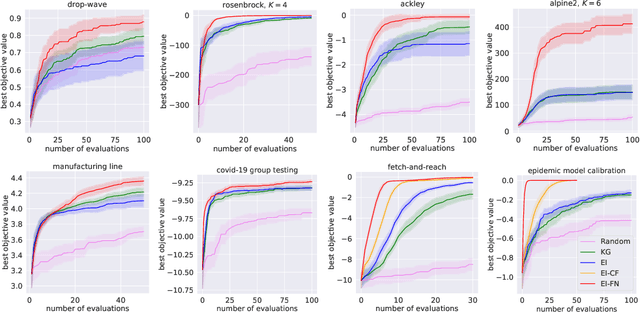
Abstract:Bayesian optimization is a framework for optimizing functions that are costly or time-consuming to evaluate. Recent work has considered Bayesian optimization of function networks (BOFN), where the objective function is computed via a network of functions, each taking as input the output of previous nodes in the network and additional parameters. Exploiting this network structure has been shown to yield significant performance improvements. Existing BOFN algorithms for general-purpose networks are required to evaluate the full network at each iteration. However, many real-world applications allow evaluating nodes individually. To take advantage of this opportunity, we propose a novel knowledge gradient acquisition function for BOFN that chooses which node to evaluate as well as the inputs for that node in a cost-aware fashion. This approach can dramatically reduce query costs by allowing the evaluation of part of the network at a lower cost relative to evaluating the entire network. We provide an efficient approach to optimizing our acquisition function and show it outperforms existing BOFN methods and other benchmarks across several synthetic and real-world problems. Our acquisition function is the first to enable cost-aware optimization of a broad class of function networks.
qEUBO: A Decision-Theoretic Acquisition Function for Preferential Bayesian Optimization
Mar 28, 2023Abstract:Preferential Bayesian optimization (PBO) is a framework for optimizing a decision maker's latent utility function using preference feedback. This work introduces the expected utility of the best option (qEUBO) as a novel acquisition function for PBO. When the decision maker's responses are noise-free, we show that qEUBO is one-step Bayes optimal and thus equivalent to the popular knowledge gradient acquisition function. We also show that qEUBO enjoys an additive constant approximation guarantee to the one-step Bayes-optimal policy when the decision maker's responses are corrupted by noise. We provide an extensive evaluation of qEUBO and demonstrate that it outperforms the state-of-the-art acquisition functions for PBO across many settings. Finally, we show that, under sufficient regularity conditions, qEUBO's Bayesian simple regret converges to zero at a rate $o(1/n)$ as the number of queries, $n$, goes to infinity. In contrast, we show that simple regret under qEI, a popular acquisition function for standard BO often used for PBO, can fail to converge to zero. Enjoying superior performance, simple computation, and a grounded decision-theoretic justification, qEUBO is a promising acquisition function for PBO.
Preference Exploration for Efficient Bayesian Optimization with Multiple Outcomes
Mar 21, 2022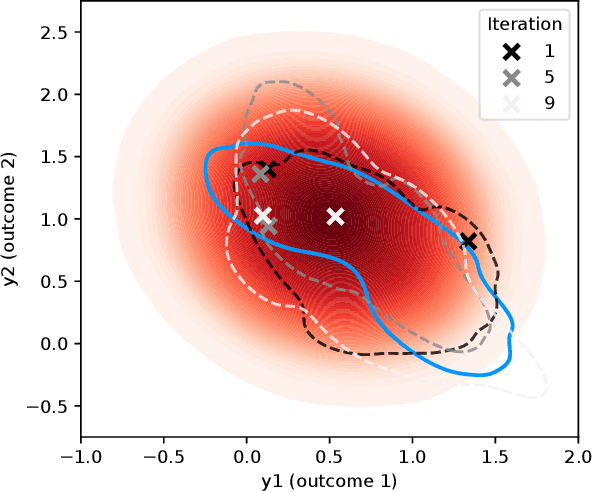


Abstract:We consider Bayesian optimization of expensive-to-evaluate experiments that generate vector-valued outcomes over which a decision-maker (DM) has preferences. These preferences are encoded by a utility function that is not known in closed form but can be estimated by asking the DM to express preferences over pairs of outcome vectors. To address this problem, we develop Bayesian optimization with preference exploration, a novel framework that alternates between interactive real-time preference learning with the DM via pairwise comparisons between outcomes, and Bayesian optimization with a learned compositional model of DM utility and outcomes. Within this framework, we propose preference exploration strategies specifically designed for this task, and demonstrate their performance via extensive simulation studies.
Thinking inside the box: A tutorial on grey-box Bayesian optimization
Jan 02, 2022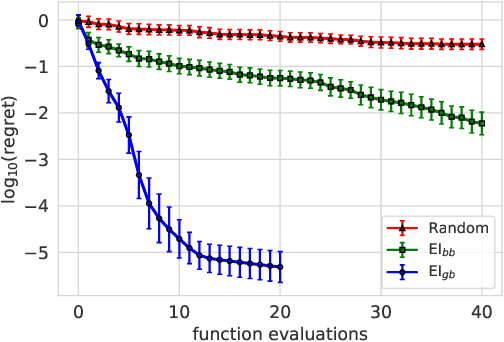
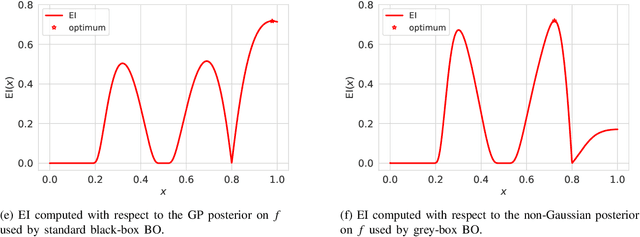
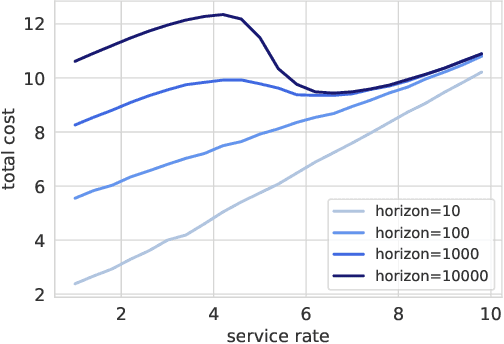
Abstract:Bayesian optimization (BO) is a framework for global optimization of expensive-to-evaluate objective functions. Classical BO methods assume that the objective function is a black box. However, internal information about objective function computation is often available. For example, when optimizing a manufacturing line's throughput with simulation, we observe the number of parts waiting at each workstation, in addition to the overall throughput. Recent BO methods leverage such internal information to dramatically improve performance. We call these "grey-box" BO methods because they treat objective computation as partially observable and even modifiable, blending the black-box approach with so-called "white-box" first-principles knowledge of objective function computation. This tutorial describes these methods, focusing on BO of composite objective functions, where one can observe and selectively evaluate individual constituents that feed into the overall objective; and multi-fidelity BO, where one can evaluate cheaper approximations of the objective function by varying parameters of the evaluation oracle.
Bayesian Optimization of Function Networks
Dec 31, 2021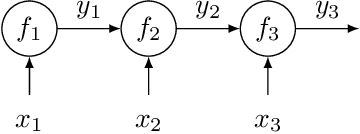
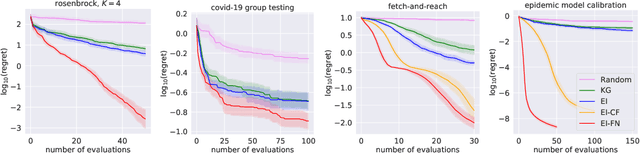
Abstract:We consider Bayesian optimization of the output of a network of functions, where each function takes as input the output of its parent nodes, and where the network takes significant time to evaluate. Such problems arise, for example, in reinforcement learning, engineering design, and manufacturing. While the standard Bayesian optimization approach observes only the final output, our approach delivers greater query efficiency by leveraging information that the former ignores: intermediate output within the network. This is achieved by modeling the nodes of the network using Gaussian processes and choosing the points to evaluate using, as our acquisition function, the expected improvement computed with respect to the implied posterior on the objective. Although the non-Gaussian nature of this posterior prevents computing our acquisition function in closed form, we show that it can be efficiently maximized via sample average approximation. In addition, we prove that our method is asymptotically consistent, meaning that it finds a globally optimal solution as the number of evaluations grows to infinity, thus generalizing previously known convergence results for the expected improvement. Notably, this holds even though our method might not evaluate the domain densely, instead leveraging problem structure to leave regions unexplored. Finally, we show that our approach dramatically outperforms standard Bayesian optimization methods in several synthetic and real-world problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge