Bayesian preference elicitation for decision support in multiobjective optimization

We present a novel approach to help decision-makers efficiently identify preferred solutions from the Pareto set of a multi-objective optimization problem. Our method uses a Bayesian model to estimate the decision-maker's utility function based on pairwise comparisons. Aided by this model, a principled elicitation strategy selects queries interactively to balance exploration and exploitation, guiding the discovery of high-utility solutions. The approach is flexible: it can be used interactively or a posteriori after estimating the Pareto front through standard multi-objective optimization techniques. Additionally, at the end of the elicitation phase, it generates a reduced menu of high-quality solutions, simplifying the decision-making process. Through experiments on test problems with up to nine objectives, our method demonstrates superior performance in finding high-utility solutions with a small number of queries. We also provide an open-source implementation of our method to support its adoption by the broader community.

Training Characteristic Functions with Reinforcement Learning: XAI-methods play Connect Four

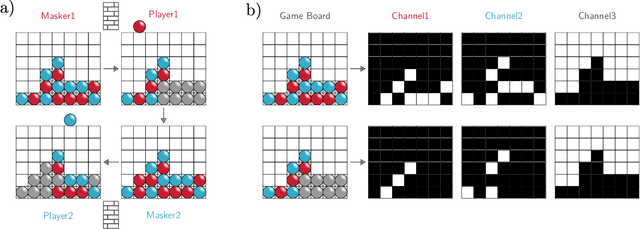
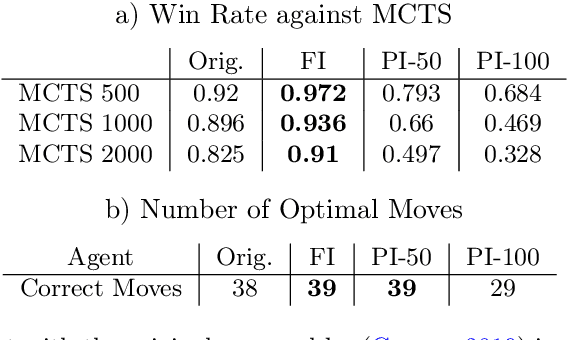
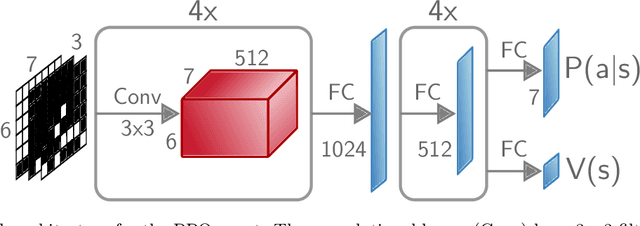
One of the goals of Explainable AI (XAI) is to determine which input components were relevant for a classifier decision. This is commonly know as saliency attribution. Characteristic functions (from cooperative game theory) are able to evaluate partial inputs and form the basis for theoretically "fair" attribution methods like Shapley values. Given only a standard classifier function, it is unclear how partial input should be realised. Instead, most XAI-methods for black-box classifiers like neural networks consider counterfactual inputs that generally lie off-manifold. This makes them hard to evaluate and easy to manipulate. We propose a setup to directly train characteristic functions in the form of neural networks to play simple two-player games. We apply this to the game of Connect Four by randomly hiding colour information from our agents during training. This has three advantages for comparing XAI-methods: It alleviates the ambiguity about how to realise partial input, makes off-manifold evaluation unnecessary and allows us to compare the methods by letting them play against each other.

Efficient Tree Solver for Hines Matrices on the GPU

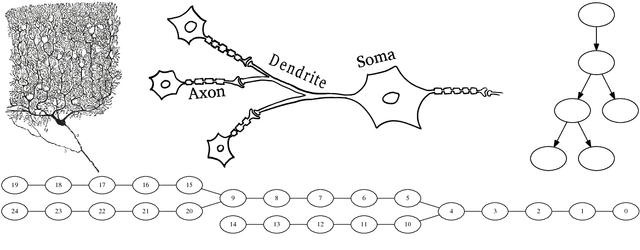
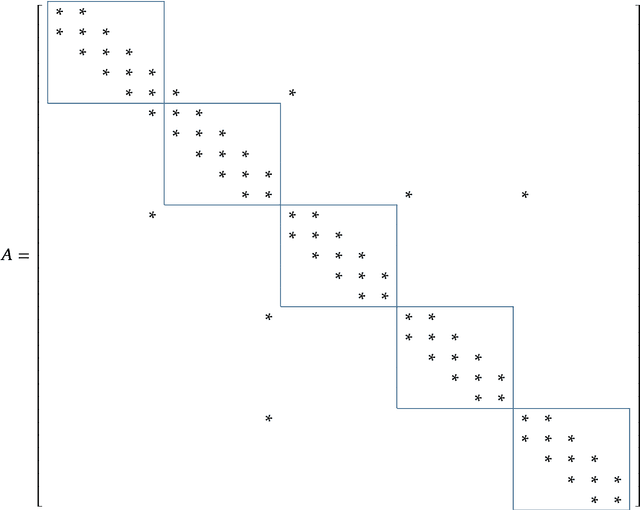
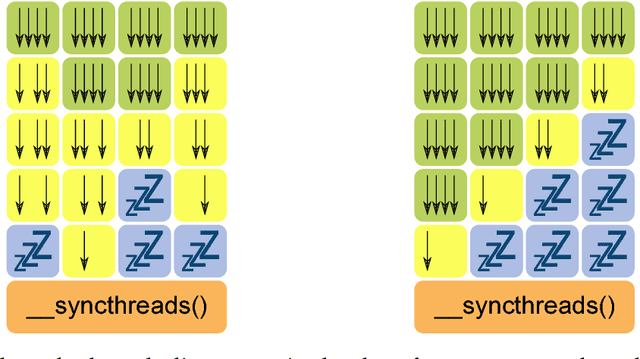
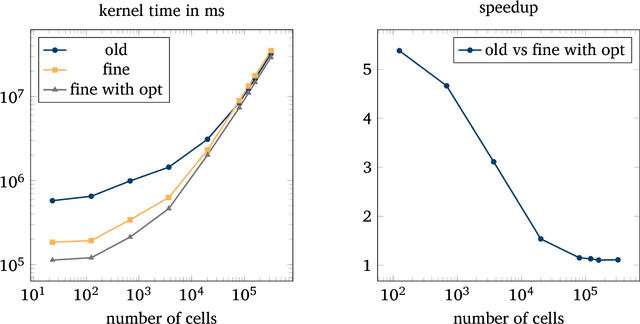
The human brain consists of a large number of interconnected neurons communicating via exchange of electrical spikes. Simulations play an important role in better understanding electrical activity in the brain and offers a way to to compare measured data to simulated data such that experimental data can be interpreted better. A key component in such simulations is an efficient solver for the Hines matrices used in computing inter-neuron signal propagation. In order to achieve high performance simulations, it is crucial to have an efficient solver algorithm. In this report we explain a new parallel GPU solver for these matrices which offers fine grained parallelization and allows for work balancing during the simulation setup.