Aaron D. Ames
Risk-Aware Safety Filters with Poisson Safety Functions and Laplace Guidance Fields
Oct 29, 2025Abstract:Robotic systems navigating in real-world settings require a semantic understanding of their environment to properly determine safe actions. This work aims to develop the mathematical underpinnings of such a representation -- specifically, the goal is to develop safety filters that are risk-aware. To this end, we take a two step approach: encoding an understanding of the environment via Poisson's equation, and associated risk via Laplace guidance fields. That is, we first solve a Dirichlet problem for Poisson's equation to generate a safety function that encodes system safety as its 0-superlevel set. We then separately solve a Dirichlet problem for Laplace's equation to synthesize a safe \textit{guidance field} that encodes variable levels of caution around obstacles -- by enforcing a tunable flux boundary condition. The safety function and guidance fields are then combined to define a safety constraint and used to synthesize a risk-aware safety filter which, given a semantic understanding of an environment with associated risk levels of environmental features, guarantees safety while prioritizing avoidance of higher risk obstacles. We demonstrate this method in simulation and discuss how \textit{a priori} understandings of obstacle risk can be directly incorporated into the safety filter to generate safe behaviors that are risk-aware.
Hierarchical Reduced-Order Model Predictive Control for Robust Locomotion on Humanoid Robots
Sep 05, 2025Abstract:As humanoid robots enter real-world environments, ensuring robust locomotion across diverse environments is crucial. This paper presents a computationally efficient hierarchical control framework for humanoid robot locomotion based on reduced-order models -- enabling versatile step planning and incorporating arm and torso dynamics to better stabilize the walking. At the high level, we use the step-to-step dynamics of the ALIP model to simultaneously optimize over step periods, step lengths, and ankle torques via nonlinear MPC. The ALIP trajectories are used as references to a linear MPC framework that extends the standard SRB-MPC to also include simplified arm and torso dynamics. We validate the performance of our approach through simulation and hardware experiments on the Unitree G1 humanoid robot. In the proposed framework the high-level step planner runs at 40 Hz and the mid-level MPC at 500 Hz using the onboard mini-PC. Adaptive step timing increased the push recovery success rate by 36%, and the upper body control improved the yaw disturbance rejection. We also demonstrate robust locomotion across diverse indoor and outdoor terrains, including grass, stone pavement, and uneven gym mats.
Compatibility of Multiple Control Barrier Functions for Constrained Nonlinear Systems
Sep 04, 2025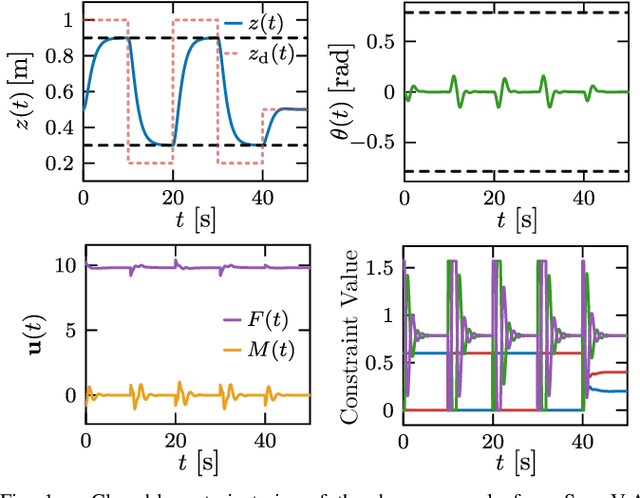
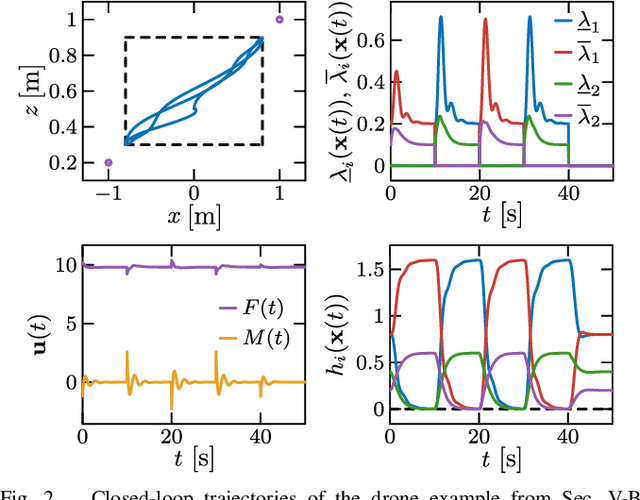
Abstract:Control barrier functions (CBFs) are a powerful tool for the constrained control of nonlinear systems; however, the majority of results in the literature focus on systems subject to a single CBF constraint, making it challenging to synthesize provably safe controllers that handle multiple state constraints. This paper presents a framework for constrained control of nonlinear systems subject to box constraints on the systems' vector-valued outputs using multiple CBFs. Our results illustrate that when the output has a vector relative degree, the CBF constraints encoding these box constraints are compatible, and the resulting optimization-based controller is locally Lipschitz continuous and admits a closed-form expression. Additional results are presented to characterize the degradation of nominal tracking objectives in the presence of safety constraints. Simulations of a planar quadrotor are presented to demonstrate the efficacy of the proposed framework.
Safe Navigation under State Uncertainty: Online Adaptation for Robust Control Barrier Functions
Aug 26, 2025Abstract:Measurements and state estimates are often imperfect in control practice, posing challenges for safety-critical applications, where safety guarantees rely on accurate state information. In the presence of estimation errors, several prior robust control barrier function (R-CBF) formulations have imposed strict conditions on the input. These methods can be overly conservative and can introduce issues such as infeasibility, high control effort, etc. This work proposes a systematic method to improve R-CBFs, and demonstrates its advantages on a tracked vehicle that navigates among multiple obstacles. A primary contribution is a new optimization-based online parameter adaptation scheme that reduces the conservativeness of existing R-CBFs. In order to reduce the complexity of the parameter optimization, we merge several safety constraints into one unified numerical CBF via Poisson's equation. We further address the dual relative degree issue that typically causes difficulty in vehicle tracking. Experimental trials demonstrate the overall performance improvement of our approach over existing formulations.
Hybrid Data-Driven Predictive Control for Robust and Reactive Exoskeleton Locomotion Synthesis
Aug 14, 2025Abstract:Robust bipedal locomotion in exoskeletons requires the ability to dynamically react to changes in the environment in real time. This paper introduces the hybrid data-driven predictive control (HDDPC) framework, an extension of the data-enabled predictive control, that addresses these challenges by simultaneously planning foot contact schedules and continuous domain trajectories. The proposed framework utilizes a Hankel matrix-based representation to model system dynamics, incorporating step-to-step (S2S) transitions to enhance adaptability in dynamic environments. By integrating contact scheduling with trajectory planning, the framework offers an efficient, unified solution for locomotion motion synthesis that enables robust and reactive walking through online replanning. We validate the approach on the Atalante exoskeleton, demonstrating improved robustness and adaptability.
Locomotion on Constrained Footholds via Layered Architectures and Model Predictive Control
Jun 11, 2025Abstract:Computing stabilizing and optimal control actions for legged locomotion in real time is difficult due to the nonlinear, hybrid, and high dimensional nature of these robots. The hybrid nature of the system introduces a combination of discrete and continuous variables which causes issues for numerical optimal control. To address these challenges, we propose a layered architecture that separates the choice of discrete variables and a smooth Model Predictive Controller (MPC). The layered formulation allows for online flexibility and optimality without sacrificing real-time performance through a combination of gradient-free and gradient-based methods. The architecture leverages a sampling-based method for determining discrete variables, and a classical smooth MPC formulation using these fixed discrete variables. We demonstrate the results on a quadrupedal robot stepping over gaps and onto terrain with varying heights. In simulation, we demonstrate the controller on a humanoid robot for gap traversal. The layered approach is shown to be more optimal and reliable than common heuristic-based approaches and faster to compute than pure sampling methods.
Bracing for Impact: Robust Humanoid Push Recovery and Locomotion with Reduced Order Models
May 16, 2025Abstract:Push recovery during locomotion will facilitate the deployment of humanoid robots in human-centered environments. In this paper, we present a unified framework for walking control and push recovery for humanoid robots, leveraging the arms for push recovery while dynamically walking. The key innovation is to use the environment, such as walls, to facilitate push recovery by combining Single Rigid Body model predictive control (SRB-MPC) with Hybrid Linear Inverted Pendulum (HLIP) dynamics to enable robust locomotion, push detection, and recovery by utilizing the robot's arms to brace against such walls and dynamically adjusting the desired contact forces and stepping patterns. Extensive simulation results on a humanoid robot demonstrate improved perturbation rejection and tracking performance compared to HLIP alone, with the robot able to recover from pushes up to 100N for 0.2s while walking at commanded speeds up to 0.5m/s. Robustness is further validated in scenarios with angled walls and multi-directional pushes.
SHIELD: Safety on Humanoids via CBFs In Expectation on Learned Dynamics
May 16, 2025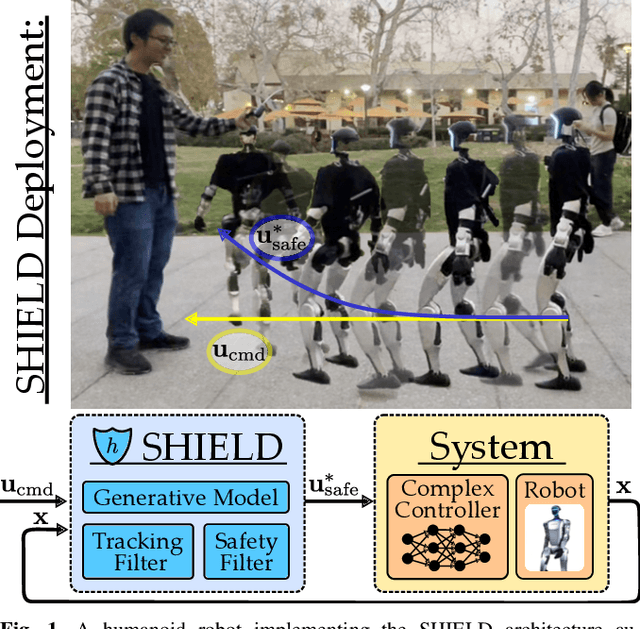

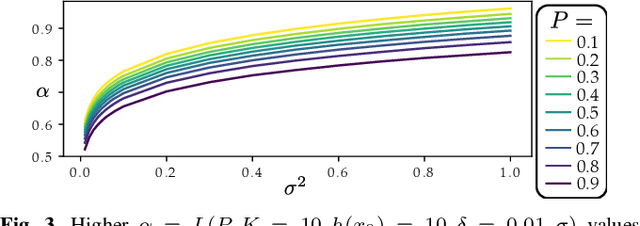
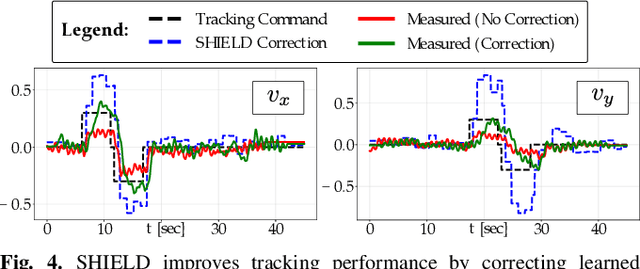
Abstract:Robot learning has produced remarkably effective ``black-box'' controllers for complex tasks such as dynamic locomotion on humanoids. Yet ensuring dynamic safety, i.e., constraint satisfaction, remains challenging for such policies. Reinforcement learning (RL) embeds constraints heuristically through reward engineering, and adding or modifying constraints requires retraining. Model-based approaches, like control barrier functions (CBFs), enable runtime constraint specification with formal guarantees but require accurate dynamics models. This paper presents SHIELD, a layered safety framework that bridges this gap by: (1) training a generative, stochastic dynamics residual model using real-world data from hardware rollouts of the nominal controller, capturing system behavior and uncertainties; and (2) adding a safety layer on top of the nominal (learned locomotion) controller that leverages this model via a stochastic discrete-time CBF formulation enforcing safety constraints in probability. The result is a minimally-invasive safety layer that can be added to the existing autonomy stack to give probabilistic guarantees of safety that balance risk and performance. In hardware experiments on an Unitree G1 humanoid, SHIELD enables safe navigation (obstacle avoidance) through varied indoor and outdoor environments using a nominal (unknown) RL controller and onboard perception.
Secure Safety Filter: Towards Safe Flight Control under Sensor Attacks
May 11, 2025Abstract:Modern autopilot systems are prone to sensor attacks that can jeopardize flight safety. To mitigate this risk, we proposed a modular solution: the secure safety filter, which extends the well-established control barrier function (CBF)-based safety filter to account for, and mitigate, sensor attacks. This module consists of a secure state reconstructor (which generates plausible states) and a safety filter (which computes the safe control input that is closest to the nominal one). Differing from existing work focusing on linear, noise-free systems, the proposed secure safety filter handles bounded measurement noise and, by leveraging reduced-order model techniques, is applicable to the nonlinear dynamics of drones. Software-in-the-loop simulations and drone hardware experiments demonstrate the effectiveness of the secure safety filter in rendering the system safe in the presence of sensor attacks.
Dynamic Safety in Complex Environments: Synthesizing Safety Filters with Poisson's Equation
May 11, 2025Abstract:Synthesizing safe sets for robotic systems operating in complex and dynamically changing environments is a challenging problem. Solving this problem can enable the construction of safety filters that guarantee safe control actions -- most notably by employing Control Barrier Functions (CBFs). This paper presents an algorithm for generating safe sets from perception data by leveraging elliptic partial differential equations, specifically Poisson's equation. Given a local occupancy map, we solve Poisson's equation subject to Dirichlet boundary conditions, with a novel forcing function. Specifically, we design a smooth guidance vector field, which encodes gradient information required for safety. The result is a variational problem for which the unique minimizer -- a safety function -- characterizes the safe set. After establishing our theoretical result, we illustrate how safety functions can be used in CBF-based safety filtering. The real-time utility of our synthesis method is highlighted through hardware demonstrations on quadruped and humanoid robots navigating dynamically changing obstacle-filled environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge