Fast Bayesian Optimization of Function Networks with Partial Evaluations

Bayesian optimization of function networks (BOFN) is a framework for optimizing expensive-to-evaluate objective functions structured as networks, where some nodes' outputs serve as inputs for others. Many real-world applications, such as manufacturing and drug discovery, involve function networks with additional properties - nodes that can be evaluated independently and incur varying costs. A recent BOFN variant, p-KGFN, leverages this structure and enables cost-aware partial evaluations, selectively querying only a subset of nodes at each iteration. p-KGFN reduces the number of expensive objective function evaluations needed but has a large computational overhead: choosing where to evaluate requires optimizing a nested Monte Carlo-based acquisition function for each node in the network. To address this, we propose an accelerated p-KGFN algorithm that reduces computational overhead with only a modest loss in query efficiency. Key to our approach is generation of node-specific candidate inputs for each node in the network via one inexpensive global Monte Carlo simulation. Numerical experiments show that our method maintains competitive query efficiency while achieving up to a 16x speedup over the original p-KGFN algorithm.

Bayesian Optimization of Function Networks with Partial Evaluations

Bayesian optimization is a framework for optimizing functions that are costly or time-consuming to evaluate. Recent work has considered Bayesian optimization of function networks (BOFN), where the objective function is computed via a network of functions, each taking as input the output of previous nodes in the network and additional parameters. Exploiting this network structure has been shown to yield significant performance improvements. Existing BOFN algorithms for general-purpose networks are required to evaluate the full network at each iteration. However, many real-world applications allow evaluating nodes individually. To take advantage of this opportunity, we propose a novel knowledge gradient acquisition function for BOFN that chooses which node to evaluate as well as the inputs for that node in a cost-aware fashion. This approach can dramatically reduce query costs by allowing the evaluation of part of the network at a lower cost relative to evaluating the entire network. We provide an efficient approach to optimizing our acquisition function and show it outperforms existing BOFN methods and other benchmarks across several synthetic and real-world problems. Our acquisition function is the first to enable cost-aware optimization of a broad class of function networks.

Kernels over Sets of Finite Sets using RKHS Embeddings, with Application to Bayesian Optimization

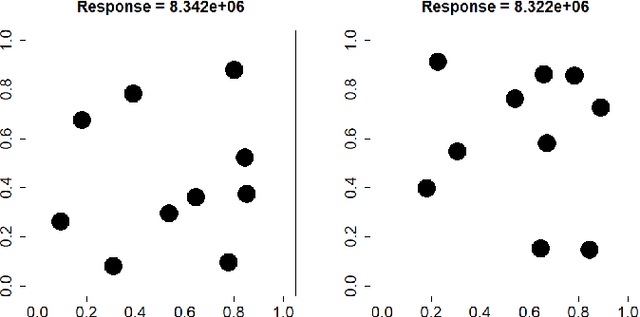
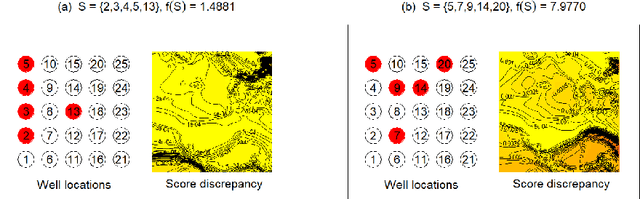
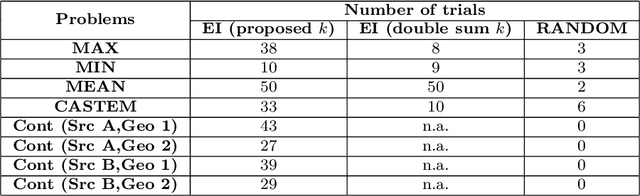
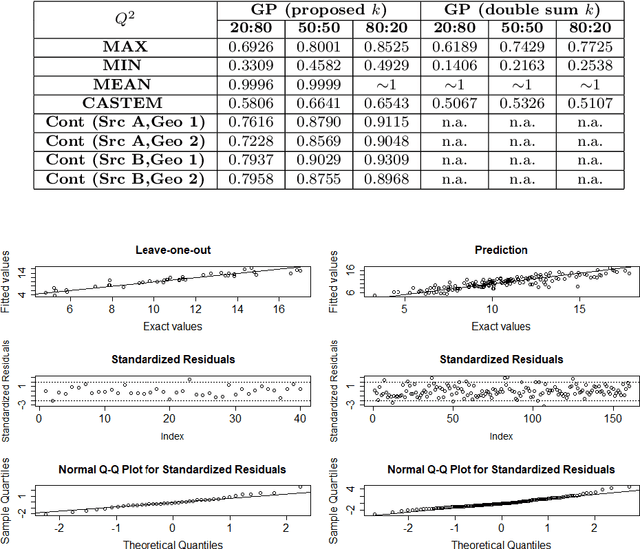
We focus on kernel methods for set-valued inputs and their application to Bayesian set optimization, notably combinatorial optimization. We introduce a class of (strictly) positive definite kernels that relies on Reproducing Kernel Hilbert Space embeddings, and successfully generalizes "double sum" set kernels recently considered in Bayesian set optimization, which turn out to be unsuitable for combinatorial optimization. The proposed class of kernels, for which we provide theoretical guarantees, essentially consists in applying an outer kernel on top of the canonical distance induced by a double sum kernel. Proofs of theoretical results about considered kernels are complemented by a few practicalities regarding hyperparameter fitting. We furthermore demonstrate the applicability of our approach in prediction and optimization tasks, relying both on toy examples and on two test cases from mechanical engineering and hydrogeology, respectively. Experimental results illustrate the added value of the approach and open new perspectives in prediction and sequential design with set inputs.