Does Generation Require Memorization? Creative Diffusion Models using Ambient Diffusion

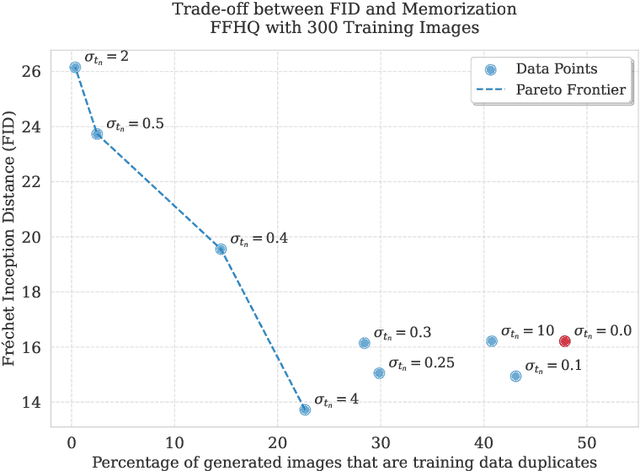
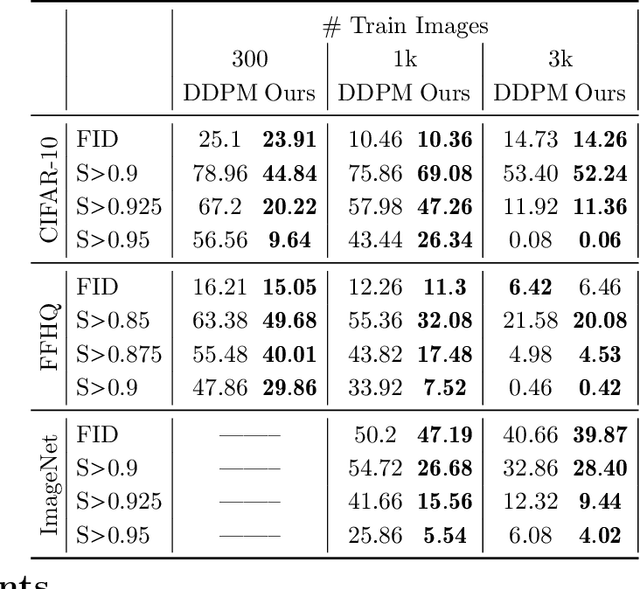
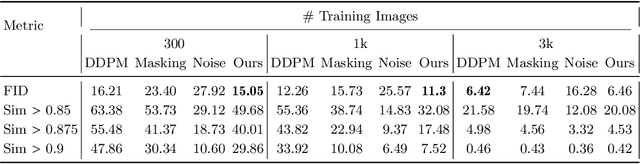
There is strong empirical evidence that the state-of-the-art diffusion modeling paradigm leads to models that memorize the training set, especially when the training set is small. Prior methods to mitigate the memorization problem often lead to a decrease in image quality. Is it possible to obtain strong and creative generative models, i.e., models that achieve high generation quality and low memorization? Despite the current pessimistic landscape of results, we make significant progress in pushing the trade-off between fidelity and memorization. We first provide theoretical evidence that memorization in diffusion models is only necessary for denoising problems at low noise scales (usually used in generating high-frequency details). Using this theoretical insight, we propose a simple, principled method to train the diffusion models using noisy data at large noise scales. We show that our method significantly reduces memorization without decreasing the image quality, for both text-conditional and unconditional models and for a variety of data availability settings.

Train for the Worst, Plan for the Best: Understanding Token Ordering in Masked Diffusions

In recent years, masked diffusion models (MDMs) have emerged as a promising alternative approach for generative modeling over discrete domains. Compared to autoregressive models (ARMs), MDMs trade off complexity at training time with flexibility at inference time. At training time, they must learn to solve an exponentially large number of infilling problems, but at inference time, they can decode tokens in essentially arbitrary order. In this work, we closely examine these two competing effects. On the training front, we theoretically and empirically demonstrate that MDMs indeed train on computationally intractable subproblems compared to their autoregressive counterparts. On the inference front, we show that a suitable strategy for adaptively choosing the token decoding order significantly enhances the capabilities of MDMs, allowing them to sidestep hard subproblems. On logic puzzles like Sudoku, we show that adaptive inference can boost solving accuracy in pretrained MDMs from $<7$% to $\approx 90$%, even outperforming ARMs with $7\times$ as many parameters and that were explicitly trained via teacher forcing to learn the right order of decoding.

Causal Language Modeling Can Elicit Search and Reasoning Capabilities on Logic Puzzles

Causal language modeling using the Transformer architecture has yielded remarkable capabilities in Large Language Models (LLMs) over the last few years. However, the extent to which fundamental search and reasoning capabilities emerged within LLMs remains a topic of ongoing debate. In this work, we study if causal language modeling can learn a complex task such as solving Sudoku puzzles. To solve a Sudoku, the model is first required to search over all empty cells of the puzzle to decide on a cell to fill and then apply an appropriate strategy to fill the decided cell. Sometimes, the application of a strategy only results in thinning down the possible values in a cell rather than concluding the exact value of the cell. In such cases, multiple strategies are applied one after the other to fill a single cell. We observe that Transformer models trained on this synthetic task can indeed learn to solve Sudokus (our model solves $94.21\%$ of the puzzles fully correctly) when trained on a logical sequence of steps taken by a solver. We find that training Transformers with the logical sequence of steps is necessary and without such training, they fail to learn Sudoku. We also extend our analysis to Zebra puzzles (known as Einstein puzzles) and show that the model solves $92.04 \%$ of the puzzles fully correctly. In addition, we study the internal representations of the trained Transformer and find that through linear probing, we can decode information about the set of possible values in any given cell from them, pointing to the presence of a strong reasoning engine implicit in the Transformer weights.

Learning general Gaussian mixtures with efficient score matching

We study the problem of learning mixtures of $k$ Gaussians in $d$ dimensions. We make no separation assumptions on the underlying mixture components: we only require that the covariance matrices have bounded condition number and that the means and covariances lie in a ball of bounded radius. We give an algorithm that draws $d^{\mathrm{poly}(k/\varepsilon)}$ samples from the target mixture, runs in sample-polynomial time, and constructs a sampler whose output distribution is $\varepsilon$-far from the unknown mixture in total variation. Prior works for this problem either (i) required exponential runtime in the dimension $d$, (ii) placed strong assumptions on the instance (e.g., spherical covariances or clusterability), or (iii) had doubly exponential dependence on the number of components $k$. Our approach departs from commonly used techniques for this problem like the method of moments. Instead, we leverage a recently developed reduction, based on diffusion models, from distribution learning to a supervised learning task called score matching. We give an algorithm for the latter by proving a structural result showing that the score function of a Gaussian mixture can be approximated by a piecewise-polynomial function, and there is an efficient algorithm for finding it. To our knowledge, this is the first example of diffusion models achieving a state-of-the-art theoretical guarantee for an unsupervised learning task.

Simple Mechanisms for Representing, Indexing and Manipulating Concepts

Deep networks typically learn concepts via classifiers, which involves setting up a model and training it via gradient descent to fit the concept-labeled data. We will argue instead that learning a concept could be done by looking at its moment statistics matrix to generate a concrete representation or signature of that concept. These signatures can be used to discover structure across the set of concepts and could recursively produce higher-level concepts by learning this structure from those signatures. When the concepts are `intersected', signatures of the concepts can be used to find a common theme across a number of related `intersected' concepts. This process could be used to keep a dictionary of concepts so that inputs could correctly identify and be routed to the set of concepts involved in the (latent) generation of the input.

Learning Mixtures of Gaussians Using the DDPM Objective

Recent works have shown that diffusion models can learn essentially any distribution provided one can perform score estimation. Yet it remains poorly understood under what settings score estimation is possible, let alone when practical gradient-based algorithms for this task can provably succeed. In this work, we give the first provably efficient results along these lines for one of the most fundamental distribution families, Gaussian mixture models. We prove that gradient descent on the denoising diffusion probabilistic model (DDPM) objective can efficiently recover the ground truth parameters of the mixture model in the following two settings: 1) We show gradient descent with random initialization learns mixtures of two spherical Gaussians in $d$ dimensions with $1/\text{poly}(d)$-separated centers. 2) We show gradient descent with a warm start learns mixtures of $K$ spherical Gaussians with $\Omega(\sqrt{\log(\min(K,d))})$-separated centers. A key ingredient in our proofs is a new connection between score-based methods and two other approaches to distribution learning, the EM algorithm and spectral methods.

Ambient Diffusion: Learning Clean Distributions from Corrupted Data

We present the first diffusion-based framework that can learn an unknown distribution using only highly-corrupted samples. This problem arises in scientific applications where access to uncorrupted samples is impossible or expensive to acquire. Another benefit of our approach is the ability to train generative models that are less likely to memorize individual training samples since they never observe clean training data. Our main idea is to introduce additional measurement distortion during the diffusion process and require the model to predict the original corrupted image from the further corrupted image. We prove that our method leads to models that learn the conditional expectation of the full uncorrupted image given this additional measurement corruption. This holds for any corruption process that satisfies some technical conditions (and in particular includes inpainting and compressed sensing). We train models on standard benchmarks (CelebA, CIFAR-10 and AFHQ) and show that we can learn the distribution even when all the training samples have $90\%$ of their pixels missing. We also show that we can finetune foundation models on small corrupted datasets (e.g. MRI scans with block corruptions) and learn the clean distribution without memorizing the training set.

RISAN: Robust Instance Specific Abstention Network

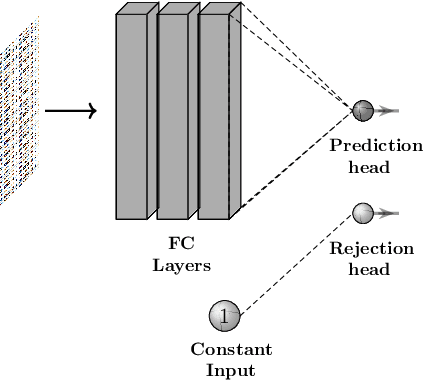
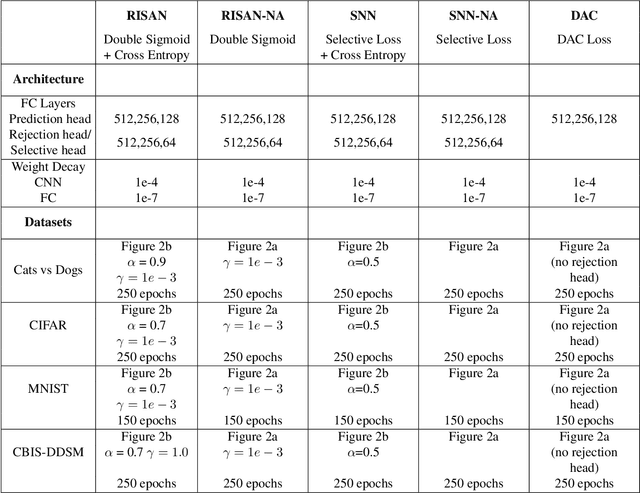
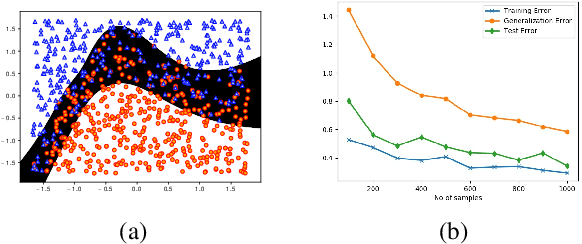
In this paper, we propose deep architectures for learning instance specific abstain (reject option) binary classifiers. The proposed approach uses double sigmoid loss function as described by Kulin Shah and Naresh Manwani in ("Online Active Learning of Reject Option Classifiers", AAAI, 2020), as a performance measure. We show that the double sigmoid loss is classification calibrated. We also show that the excess risk of 0-d-1 loss is upper bounded by the excess risk of double sigmoid loss. We derive the generalization error bounds for the proposed architecture for reject option classifiers. To show the effectiveness of the proposed approach, we experiment with several real world datasets. We observe that the proposed approach not only performs comparable to the state-of-the-art approaches, it is also robust against label noise. We also provide visualizations to observe the important features learned by the network corresponding to the abstaining decision.

Learning and Generalization in Overparameterized Normalizing Flows

In supervised learning, it is known that overparameterized neural networks with one hidden layer provably and efficiently learn and generalize, when trained using stochastic gradient descent with sufficiently small learning rate and suitable initialization. In contrast, the benefit of overparameterization in unsupervised learning is not well understood. Normalizing flows (NFs) constitute an important class of models in unsupervised learning for sampling and density estimation. In this paper, we theoretically and empirically analyze these models when the underlying neural network is one-hidden-layer overparameterized network. Our main contributions are two-fold: (1) On the one hand, we provide theoretical and empirical evidence that for a class of NFs containing most of the existing NF models, overparametrization hurts training. (2) On the other hand, we prove that unconstrained NFs, a recently introduced model, can efficiently learn any reasonable data distribution under minimal assumptions when the underlying network is overparametrized.

Rawlsian Fair Adaptation of Deep Learning Classifiers

Group-fairness in classification aims for equality of a predictive utility across different sensitive sub-populations, e.g., race or gender. Equality or near-equality constraints in group-fairness often worsen not only the aggregate utility but also the utility for the least advantaged sub-population. In this paper, we apply the principles of Pareto-efficiency and least-difference to the utility being accuracy, as an illustrative example, and arrive at the Rawls classifier that minimizes the error rate on the worst-off sensitive sub-population. Our mathematical characterization shows that the Rawls classifier uniformly applies a threshold to an ideal score of features, in the spirit of fair equality of opportunity. In practice, such a score or a feature representation is often computed by a black-box model that has been useful but unfair. Our second contribution is practical Rawlsian fair adaptation of any given black-box deep learning model, without changing the score or feature representation it computes. Given any score function or feature representation and only its second-order statistics on the sensitive sub-populations, we seek a threshold classifier on the given score or a linear threshold classifier on the given feature representation that achieves the Rawls error rate restricted to this hypothesis class. Our technical contribution is to formulate the above problems using ambiguous chance constraints, and to provide efficient algorithms for Rawlsian fair adaptation, along with provable upper bounds on the Rawls error rate. Our empirical results show significant improvement over state-of-the-art group-fair algorithms, even without retraining for fairness.