On The Verification of Neural ODEs with Stochastic Guarantees

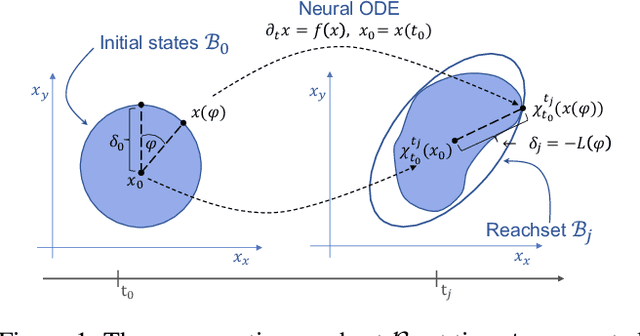
We show that Neural ODEs, an emerging class of time-continuous neural networks, can be verified by solving a set of global-optimization problems. For this purpose, we introduce Stochastic Lagrangian Reachability (SLR), an abstraction-based technique for constructing a tight Reachtube (an over-approximation of the set of reachable states over a given time-horizon), and provide stochastic guarantees in the form of confidence intervals for the Reachtube bounds. SLR inherently avoids the infamous wrapping effect (accumulation of over-approximation errors) by performing local optimization steps to expand safe regions instead of repeatedly forward-propagating them as is done by deterministic reachability methods. To enable fast local optimizations, we introduce a novel forward-mode adjoint sensitivity method to compute gradients without the need for backpropagation. Finally, we establish asymptotic and non-asymptotic convergence rates for SLR.

Lagrangian Reachtubes: The Next Generation

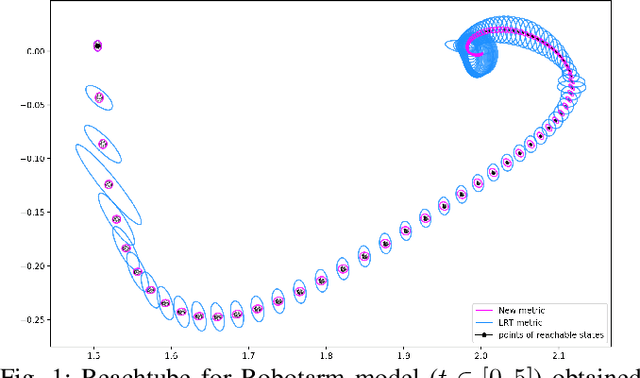
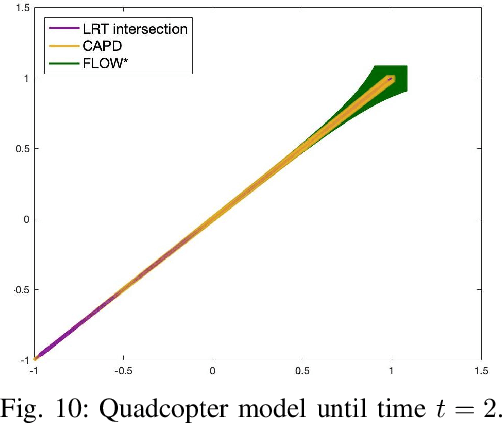
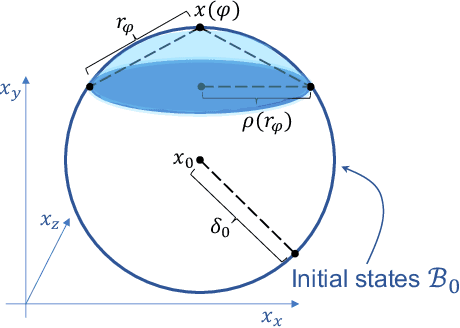
We introduce LRT-NG, a set of techniques and an associated toolset that computes a reachtube (an over-approximation of the set of reachable states over a given time horizon) of a nonlinear dynamical system. LRT-NG significantly advances the state-of-the-art Langrangian Reachability and its associated tool LRT. From a theoretical perspective, LRT-NG is superior to LRT in three ways. First, it uses for the first time an analytically computed metric for the propagated ball which is proven to minimize the ball's volume. We emphasize that the metric computation is the centerpiece of all bloating-based techniques. Secondly, it computes the next reachset as the intersection of two balls: one based on the Cartesian metric and the other on the new metric. While the two metrics were previously considered opposing approaches, their joint use considerably tightens the reachtubes. Thirdly, it avoids the "wrapping effect" associated with the validated integration of the center of the reachset, by optimally absorbing the interval approximation in the radius of the next ball. From a tool-development perspective, LRT-NG is superior to LRT in two ways. First, it is a standalone tool that no longer relies on CAPD. This required the implementation of the Lohner method and a Runge-Kutta time-propagation method. Secondly, it has an improved interface, allowing the input model and initial conditions to be provided as external input files. Our experiments on a comprehensive set of benchmarks, including two Neural ODEs, demonstrates LRT-NG's superior performance compared to LRT, CAPD, and Flow*.

Liquid Time-constant Networks

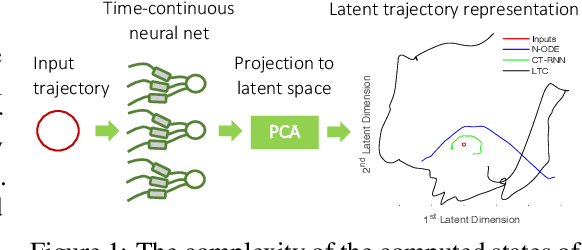
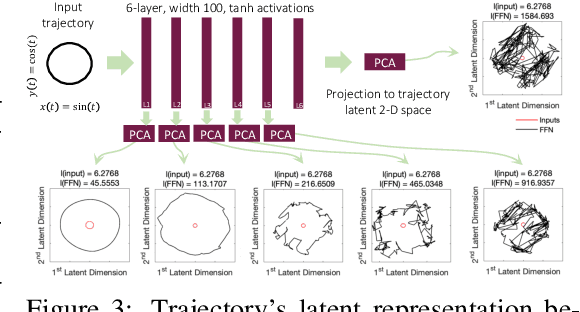
We introduce a new class of time-continuous recurrent neural network models. Instead of declaring the nonlinearity of a learning system by neurons, we impose specialized nonlinearities on the network connections. The obtained models realize dynamical systems with varying (i.e., \emph{liquid}) time-constants coupled to their hidden state, and outputs being computed by numerical differential equation solvers. These neural networks exhibit stable and bounded behavior, yield superior expressivity within the family of neural ordinary differential equations, and give rise to improved performance on time-series prediction tasks. To demonstrate these properties, we first take a theoretical approach to find bounds over their dynamics, and compute their expressive power by the \emph{trajectory length} measure in a latent trajectory representation space. We then conduct a series of time-series prediction experiments to manifest the approximation capability of Liquid Time-Constant Networks (LTCs) compared to classical and modern RNNs.

ResNets, NeuralODEs and CT-RNNs are Particular Neural Regulatory Networks

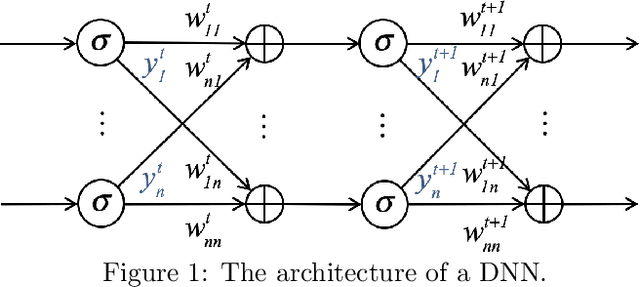
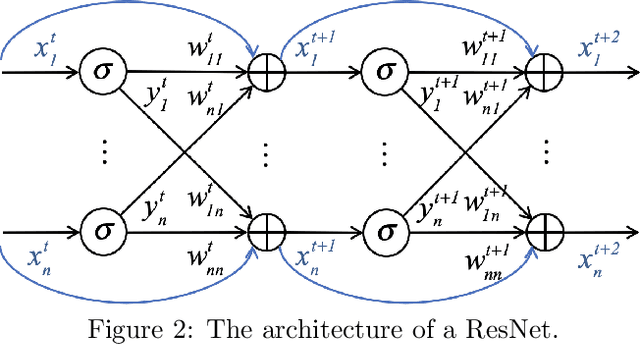
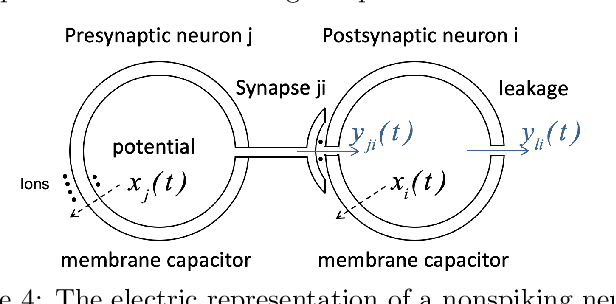
This paper shows that ResNets, NeuralODEs, and CT-RNNs, are particular neural regulatory networks (NRNs), a biophysical model for the nonspiking neurons encountered in small species, such as the C.elegans nematode, and in the retina of large species. Compared to ResNets, NeuralODEs and CT-RNNs, NRNs have an additional multiplicative term in their synaptic computation, allowing them to adapt to each particular input. This additional flexibility makes NRNs $M$ times more succinct than NeuralODEs and CT-RNNs, where $M$ is proportional to the size of the training set. Moreover, as NeuralODEs and CT-RNNs are $N$ times more succinct than ResNets, where $N$ is the number of integration steps required to compute the output $F(x)$ for a given input $x$, NRNs are in total $M\,{\cdot}\,N$ more succinct than ResNets. For a given approximation task, this considerable succinctness allows to learn a very small and therefore understandable NRN, whose behavior can be explained in terms of well established architectural motifs, that NRNs share with gene regulatory networks, such as, activation, inhibition, sequentialization, mutual exclusion, and synchronization. To the best of our knowledge, this paper unifies for the first time the mainstream work on deep neural networks with the one in biology and neuroscience in a quantitative fashion.

A Nonparametric Bayesian Model for Sparse Temporal Multigraphs

As the availability and importance of temporal interaction data--such as email communication--increases, it becomes increasingly important to understand the underlying structure that underpins these interactions. Often these interactions form a multigraph, where we might have multiple interactions between two entities. Such multigraphs tend to be sparse yet structured, and their distribution often evolves over time. Existing statistical models with interpretable parameters can capture some, but not all, of these properties. We propose a dynamic nonparametric model for interaction multigraphs that combines the sparsity of edge-exchangeable multigraphs with dynamic clustering patterns that tend to reinforce recent behavioral patterns. We show that our method yields improved held-out likelihood over stationary variants, and impressive predictive performance against a range of state-of-the-art dynamic graph models.

Neural Simplex Architecture

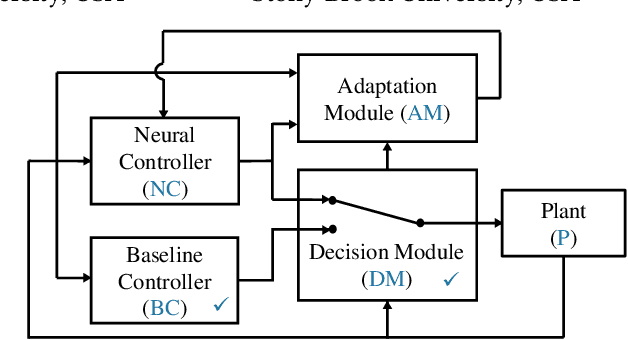
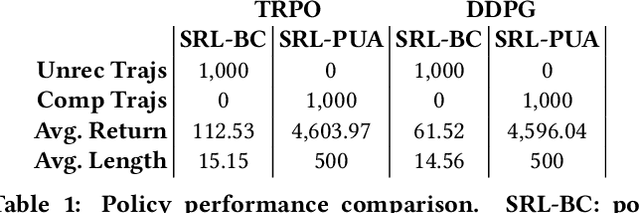
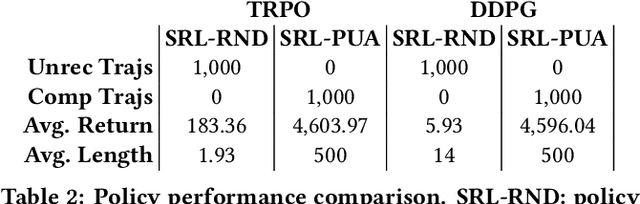
We present the Neural Simplex Architecture (NSA), a new approach to runtime assurance that provides safety guarantees for neural controllers (obtained e.g. using reinforcement learning) of complex autonomous and other cyber-physical systems without unduly sacrificing performance. NSA is inspired by the Simplex control architecture of Sha et al., but with some significant differences. In the traditional Simplex approach, the advanced controller (AC) is treated as a black box; there are no techniques for correcting the AC after it generates a potentially unsafe control input that causes a failover to the BC. Our NSA addresses this limitation. NSA not only provides safety assurances for CPSs in the presence of a possibly faulty neural controller, but can also improve the safety of such a controller in an online setting via retraining, without degrading its performance. NSA also offers reverse switching strategies, which allow the AC to resume control of the system under reasonable conditions, allowing the mission to continue unabated. Our experimental results on several significant case studies, including a target-seeking ground rover navigating an obstacle field and a neural controller for an artificial pancreas system, demonstrate NSA's benefits.

Dynamic Nonparametric Edge-Clustering Model for Time-Evolving Sparse Networks

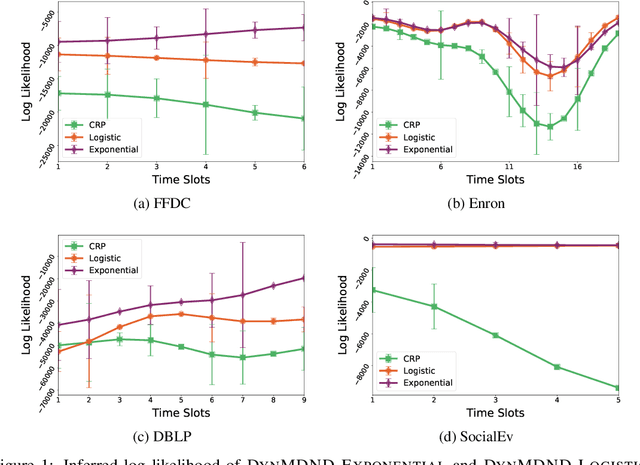
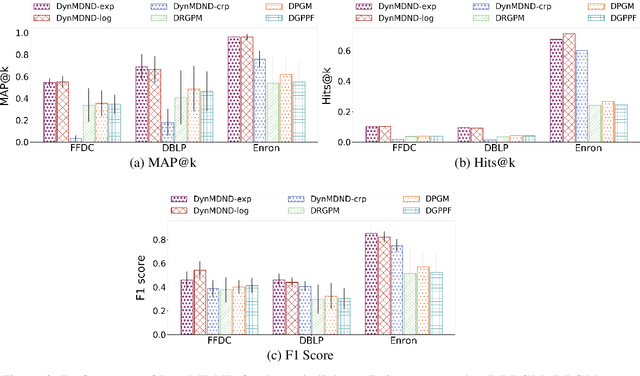
Interaction graphs, such as those recording emails between individuals or transactions between institutions, tend to be sparse yet structured, and often grow in an unbounded manner. Such behavior can be well-captured by structured, nonparametric edge-exchangeable graphs. However, such exchangeable models necessarily ignore temporal dynamics in the network. We propose a dynamic nonparametric model for interaction graphs that combine the sparsity of the exchangeable models with dynamic clustering patterns that tend to reinforce recent behavioral patterns. We show that our method yields improved held-out likelihood over stationary variants, and impressive predictive performance against a range of state-of-the-art dynamic interaction graph models.

A Roadmap Towards Resilient Internet of Things for Cyber-Physical Systems

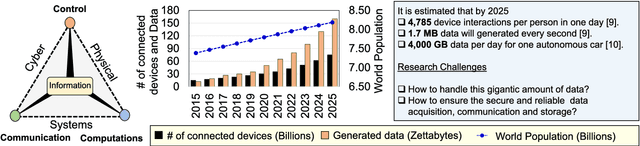
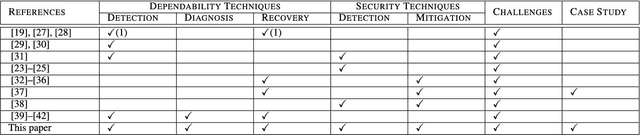
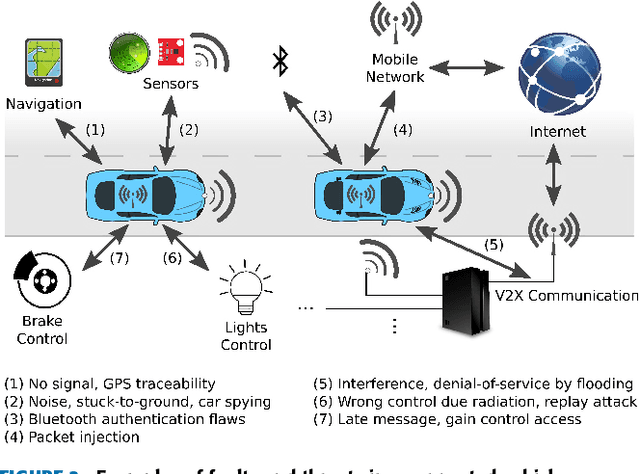
The Internet of Things (IoT) is a ubiquitous system connecting many different devices - the things - which can be accessed from the distance. The cyber-physical systems (CPS) monitor and control the things from the distance. As a result, the concepts of dependability and security get deeply intertwined. The increasing level of dynamicity, heterogeneity, and complexity adds to the system's vulnerability, and challenges its ability to react to faults. This paper summarizes state-of-the-art of existing work on anomaly detection, fault-tolerance and self-healing, and adds a number of other methods applicable to achieve resilience in an IoT. We particularly focus on non-intrusive methods ensuring data integrity in the network. Furthermore, this paper presents the main challenges in building a resilient IoT for CPS which is crucial in the era of smart CPS with enhanced connectivity (an excellent example of such a system is connected autonomous vehicles). It further summarizes our solutions, work-in-progress and future work to this topic to enable "Trustworthy IoT for CPS". Finally, this framework is illustrated on a selected use case: A smart sensor infrastructure in the transport domain.

Liquid Time-constant Recurrent Neural Networks as Universal Approximators

In this paper, we introduce the notion of liquid time-constant (LTC) recurrent neural networks (RNN)s, a subclass of continuous-time RNNs, with varying neuronal time-constant realized by their nonlinear synaptic transmission model. This feature is inspired by the communication principles in the nervous system of small species. It enables the model to approximate continuous mapping with a small number of computational units. We show that any finite trajectory of an $n$-dimensional continuous dynamical system can be approximated by the internal state of the hidden units and $n$ output units of an LTC network. Here, we also theoretically find bounds on their neuronal states and varying time-constant.

Re-purposing Compact Neuronal Circuit Policies to Govern Reinforcement Learning Tasks

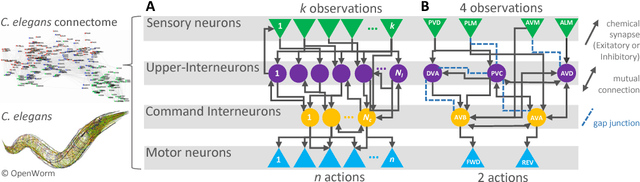
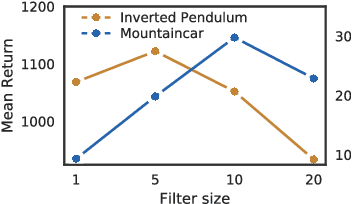
We propose an effective method for creating interpretable control agents, by \textit{re-purposing} the function of a biological neural circuit model, to govern simulated and real world reinforcement learning (RL) test-beds. Inspired by the structure of the nervous system of the soil-worm, \emph{C. elegans}, we introduce \emph{Neuronal Circuit Policies} (NCPs) as a novel recurrent neural network instance with liquid time-constants, universal approximation capabilities and interpretable dynamics. We theoretically show that they can approximate any finite simulation time of a given continuous n-dimensional dynamical system, with $n$ output units and some hidden units. We model instances of the policies and learn their synaptic and neuronal parameters to control standard RL tasks and demonstrate its application for autonomous parking of a real rover robot on a pre-defined trajectory. For reconfiguration of the \emph{purpose} of the neural circuit, we adopt a search-based RL algorithm. We show that our neuronal circuit policies perform as good as deep neural network policies with the advantage of realizing interpretable dynamics at the cell-level. We theoretically find bounds for the time-varying dynamics of the circuits, and introduce a novel way to reason about networks' dynamics.