Sophie Gruenbacher
GoTube: Scalable Stochastic Verification of Continuous-Depth Models
Jul 18, 2021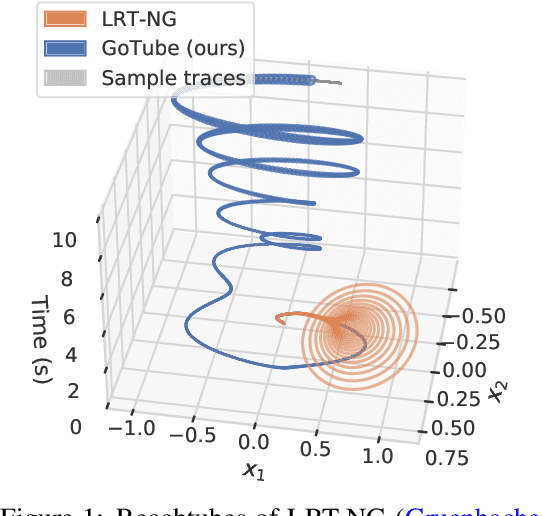
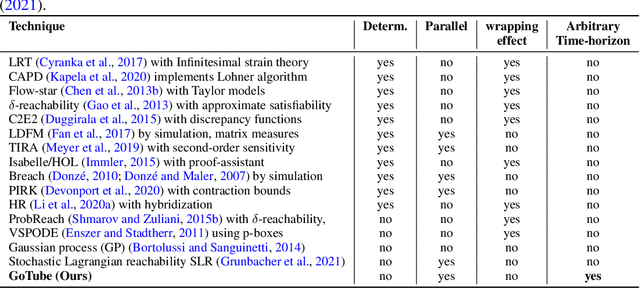
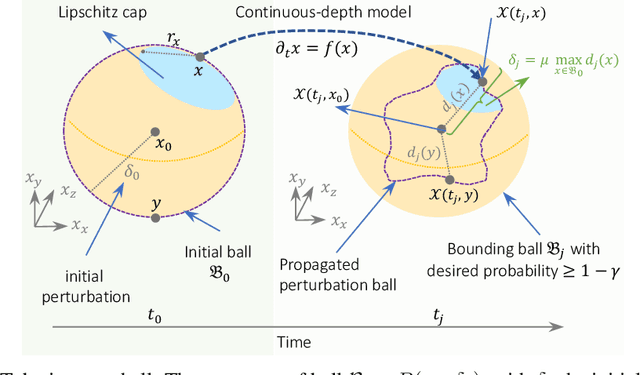
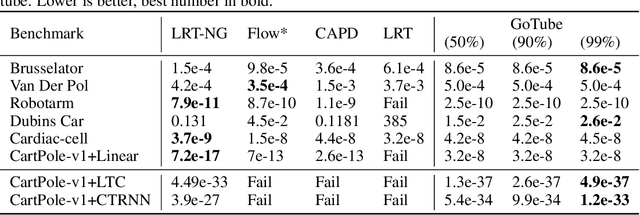
Abstract:We introduce a new stochastic verification algorithm that formally quantifies the behavioral robustness of any time-continuous process formulated as a continuous-depth model. The algorithm solves a set of global optimization (Go) problems over a given time horizon to construct a tight enclosure (Tube) of the set of all process executions starting from a ball of initial states. We call our algorithm GoTube. Through its construction, GoTube ensures that the bounding tube is conservative up to a desired probability. GoTube is implemented in JAX and optimized to scale to complex continuous-depth models. Compared to advanced reachability analysis tools for time-continuous neural networks, GoTube provably does not accumulate over-approximation errors between time steps and avoids the infamous wrapping effect inherent in symbolic techniques. We show that GoTube substantially outperforms state-of-the-art verification tools in terms of the size of the initial ball, speed, time-horizon, task completion, and scalability, on a large set of experiments. GoTube is stable and sets the state-of-the-art for its ability to scale up to time horizons well beyond what has been possible before.
On The Verification of Neural ODEs with Stochastic Guarantees
Dec 16, 2020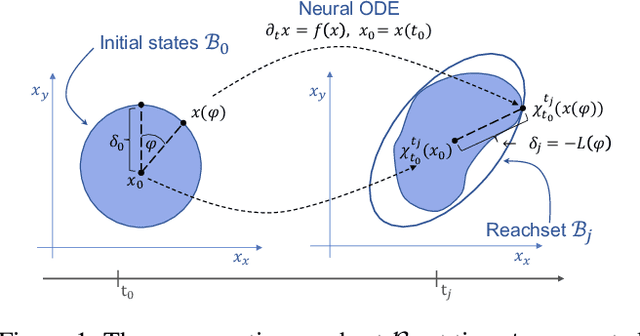
Abstract:We show that Neural ODEs, an emerging class of time-continuous neural networks, can be verified by solving a set of global-optimization problems. For this purpose, we introduce Stochastic Lagrangian Reachability (SLR), an abstraction-based technique for constructing a tight Reachtube (an over-approximation of the set of reachable states over a given time-horizon), and provide stochastic guarantees in the form of confidence intervals for the Reachtube bounds. SLR inherently avoids the infamous wrapping effect (accumulation of over-approximation errors) by performing local optimization steps to expand safe regions instead of repeatedly forward-propagating them as is done by deterministic reachability methods. To enable fast local optimizations, we introduce a novel forward-mode adjoint sensitivity method to compute gradients without the need for backpropagation. Finally, we establish asymptotic and non-asymptotic convergence rates for SLR.
Lagrangian Reachtubes: The Next Generation
Dec 14, 2020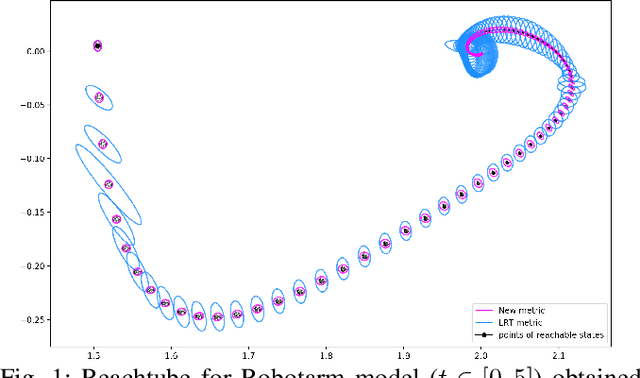
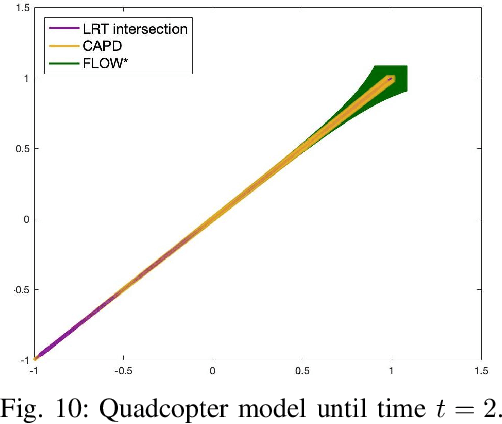


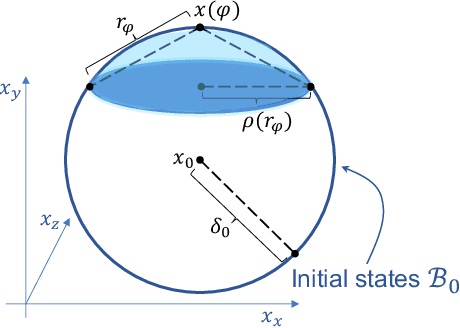
Abstract:We introduce LRT-NG, a set of techniques and an associated toolset that computes a reachtube (an over-approximation of the set of reachable states over a given time horizon) of a nonlinear dynamical system. LRT-NG significantly advances the state-of-the-art Langrangian Reachability and its associated tool LRT. From a theoretical perspective, LRT-NG is superior to LRT in three ways. First, it uses for the first time an analytically computed metric for the propagated ball which is proven to minimize the ball's volume. We emphasize that the metric computation is the centerpiece of all bloating-based techniques. Secondly, it computes the next reachset as the intersection of two balls: one based on the Cartesian metric and the other on the new metric. While the two metrics were previously considered opposing approaches, their joint use considerably tightens the reachtubes. Thirdly, it avoids the "wrapping effect" associated with the validated integration of the center of the reachset, by optimally absorbing the interval approximation in the radius of the next ball. From a tool-development perspective, LRT-NG is superior to LRT in two ways. First, it is a standalone tool that no longer relies on CAPD. This required the implementation of the Lohner method and a Runge-Kutta time-propagation method. Secondly, it has an improved interface, allowing the input model and initial conditions to be provided as external input files. Our experiments on a comprehensive set of benchmarks, including two Neural ODEs, demonstrates LRT-NG's superior performance compared to LRT, CAPD, and Flow*.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge