Quanquan Gu
Direction Matters: On the Implicit Regularization Effect of Stochastic Gradient Descent with Moderate Learning Rate
Nov 04, 2020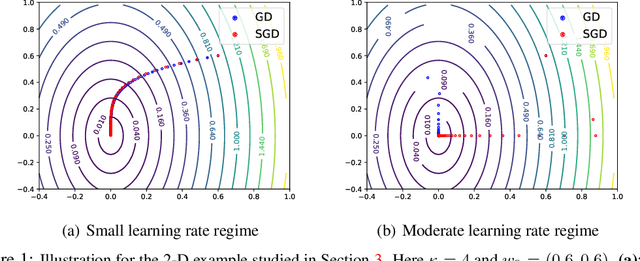
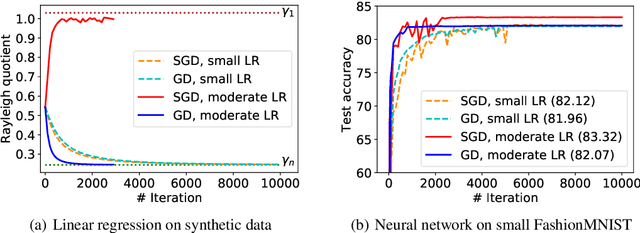
Abstract:Understanding the algorithmic regularization effect of stochastic gradient descent (SGD) is one of the key challenges in modern machine learning and deep learning theory. Most of the existing works, however, focus on very small or even infinitesimal learning rate regime, and fail to cover practical scenarios where the learning rate is moderate and annealing. In this paper, we make an initial attempt to characterize the particular regularization effect of SGD in the moderate learning rate regime by studying its behavior for optimizing an overparameterized linear regression problem. In this case, SGD and GD are known to converge to the unique minimum-norm solution; however, with the moderate and annealing learning rate, we show that they exhibit different directional bias: SGD converges along the large eigenvalue directions of the data matrix, while GD goes after the small eigenvalue directions. Furthermore, we show that such directional bias does matter when early stopping is adopted, where the SGD output is nearly optimal but the GD output is suboptimal. Finally, our theory explains several folk arts in practice used for SGD hyperparameter tuning, such as (1) linearly scaling the initial learning rate with batch size; and (2) overrunning SGD with high learning rate even when the loss stops decreasing.
Faster Convergence of Stochastic Gradient Langevin Dynamics for Non-Log-Concave Sampling
Oct 19, 2020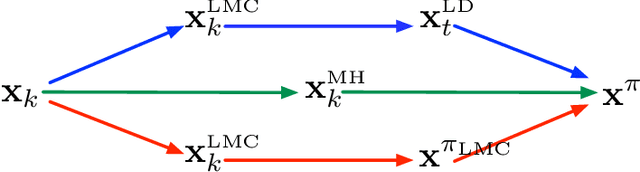
Abstract:We establish a new convergence analysis of stochastic gradient Langevin dynamics (SGLD) for sampling from a class of distributions that can be non-log-concave. At the core of our approach is a novel conductance analysis of SGLD using an auxiliary time-reversible Markov Chain. Under certain conditions on the target distribution, we prove that $\tilde O(d^4\epsilon^{-2})$ stochastic gradient evaluations suffice to guarantee $\epsilon$-sampling error in terms of the total variation distance, where $d$ is the problem dimension, which improves existing results on the convergence rate of SGLD (Raginsky et al., 2017; Xu et al., 2018). We further show that provided an additional Hessian Lipschitz condition on the log-density function, SGLD is guaranteed to achieve $\epsilon$-sampling error within $\tilde O(d^{15/4}\epsilon^{-3/2})$ stochastic gradient evaluations. Our proof technique provides a new way to study the convergence of Langevin based algorithms, and sheds some light on the design of fast stochastic gradient based sampling algorithms.
Does Network Width Really Help Adversarial Robustness?
Oct 03, 2020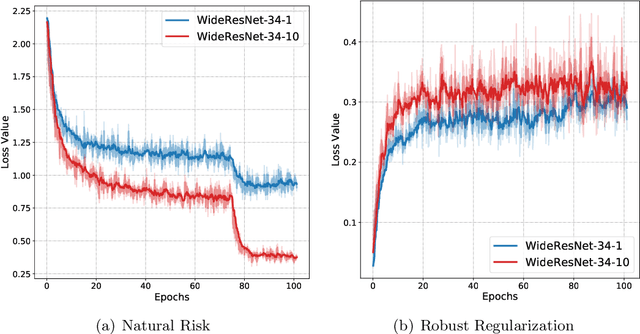
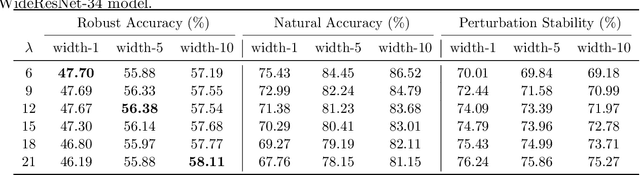
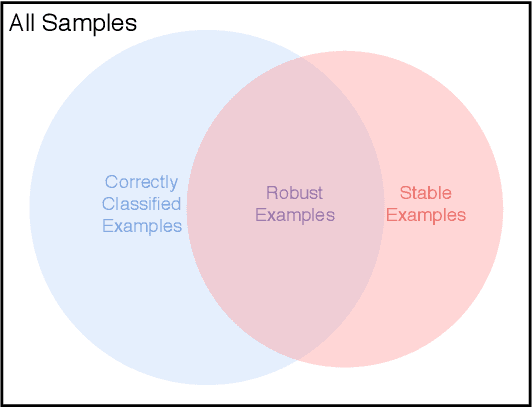
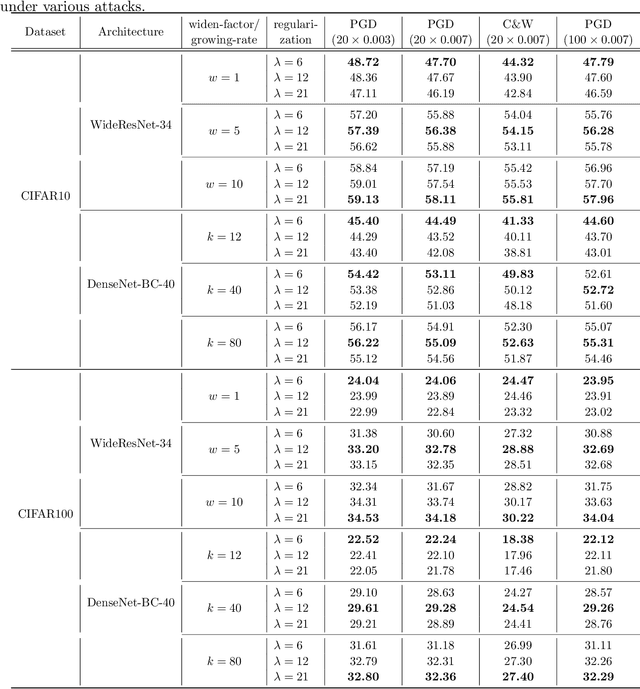
Abstract:Adversarial training is currently the most powerful defense against adversarial examples. Previous empirical results suggest that adversarial training requires wider networks for better performances. Yet, it remains elusive how does neural network width affects model robustness. In this paper, we carefully examine the relation between network width and model robustness. We present an intriguing phenomenon that the increased network width may not help robustness. Specifically, we show that the model robustness is closely related to both natural accuracy and perturbation stability, a new metric proposed in our paper to characterize the model's stability under adversarial perturbations. While better natural accuracy can be achieved on wider neural networks, the perturbation stability actually becomes worse, leading to a potentially worse overall model robustness. To understand the origin of this phenomenon, we further relate the perturbation stability with the network's local Lipschitznesss. By leveraging recent results on neural tangent kernels, we show that larger network width naturally leads to worse perturbation stability. This suggests that to fully unleash the power of wide model architecture, practitioners should adopt a larger regularization parameter for training wider networks. Experiments on benchmark datasets confirm that this strategy could indeed alleviate the perturbation stability issue and improve the state-of-the-art robust models.
Efficient Robust Training via Backward Smoothing
Oct 03, 2020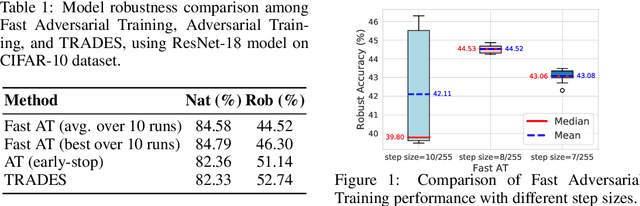
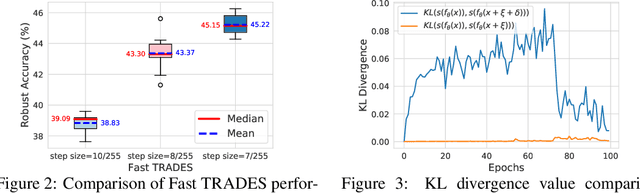

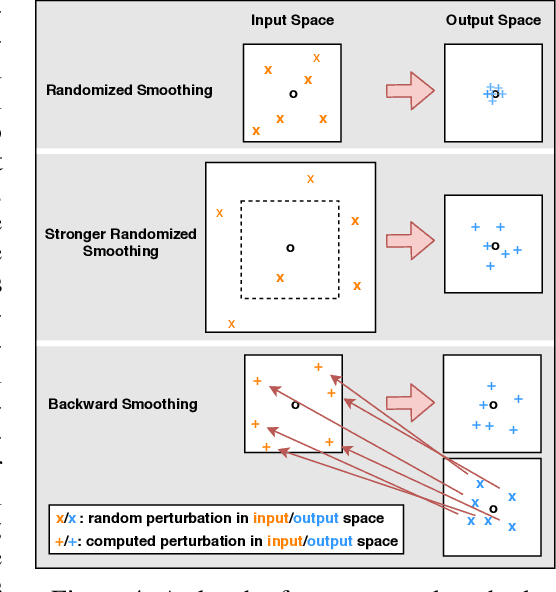
Abstract:Adversarial training is so far the most effective strategy in defending against adversarial examples. However, it suffers from high computational cost due to the iterative adversarial attacks in each training step. Recent studies show that it is possible to achieve Fast Adversarial Training by performing a single-step attack with random initialization. Yet, it remains a mystery why random initialization helps. Besides, such an approach still lags behind state-of-the-art adversarial training algorithms on both stability and model robustness. In this work, we develop a new understanding towards Fast Adversarial Training, by viewing random initialization as performing randomized smoothing for better optimization of the inner maximization problem. From this perspective, we show that the smoothing effect by random initialization is not sufficient under the adversarial perturbation constraint. A new initialization strategy, backward smoothing, is proposed to address this issue and significantly improves both stability and model robustness over single-step robust training methods.Experiments on multiple benchmarks demonstrate that our method achieves similar model robustness as the original TRADES method, while using much less training time ($\sim$3x improvement with the same training schedule).
Neural Thompson Sampling
Oct 02, 2020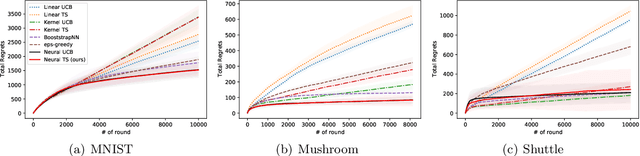
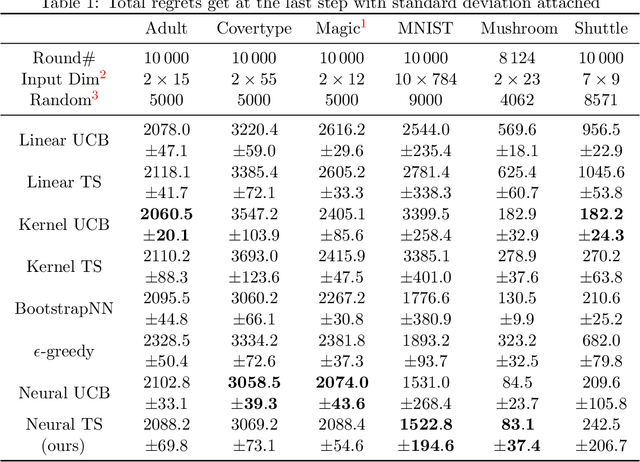
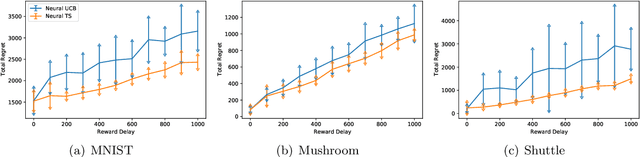
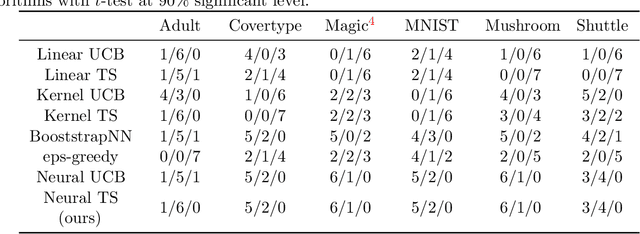
Abstract:Thompson Sampling (TS) is one of the most effective algorithms for solving contextual multi-armed bandit problems. In this paper, we propose a new algorithm, called Neural Thompson Sampling, which adapts deep neural networks for both exploration and exploitation. At the core of our algorithm is a novel posterior distribution of the reward, where its mean is the neural network approximator, and its variance is built upon the neural tangent features of the corresponding neural network. We prove that, provided the underlying reward function is bounded, the proposed algorithm is guaranteed to achieve a cumulative regret of $\mathcal{O}(T^{1/2})$, which matches the regret of other contextual bandit algorithms in terms of total round number $T$. Experimental comparisons with other benchmark bandit algorithms on various data sets corroborate our theory.
Minimax Optimal Reinforcement Learning for Discounted MDPs
Oct 01, 2020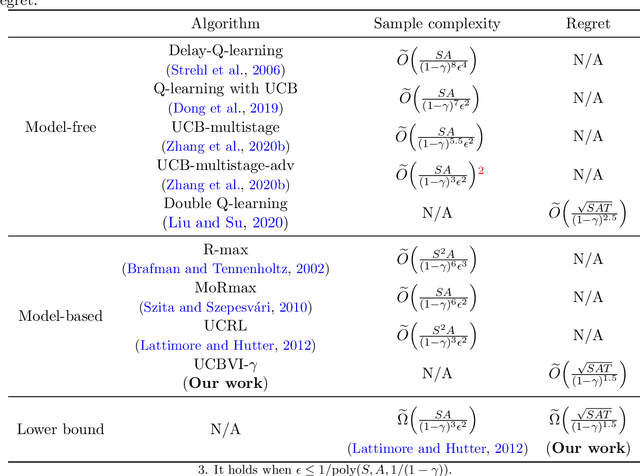
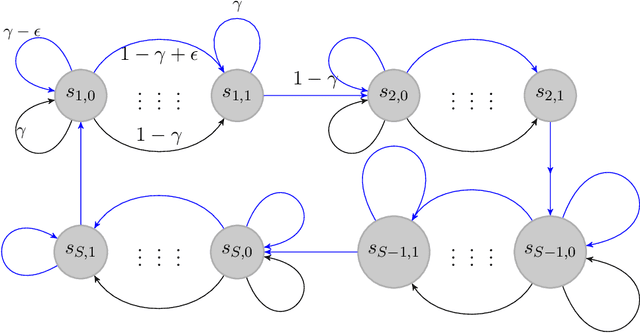
Abstract:We study the reinforcement learning problem for discounted Markov Decision Processes (MDPs) in the tabular setting. We propose a model-based algorithm named UCBVI-$\gamma$, which is based on the optimism in the face of uncertainty principle and the Bernstein-type bonus. It achieves $\tilde{O}\big({\sqrt{SAT}}/{(1-\gamma)^{1.5}}\big)$ regret, where $S$ is the number of states, $A$ is the number of actions, $\gamma$ is the discount factor and $T$ is the number of steps. In addition, we construct a class of hard MDPs and show that for any algorithm, the expected regret is at least $\tilde{\Omega}\big({\sqrt{SAT}}/{(1-\gamma)^{1.5}}\big)$. Our upper bound matches the minimax lower bound up to logarithmic factors, which suggests that UCBVI-$\gamma$ is near optimal for discounted MDPs.
Agnostic Learning of Halfspaces with Gradient Descent via Soft Margins
Oct 01, 2020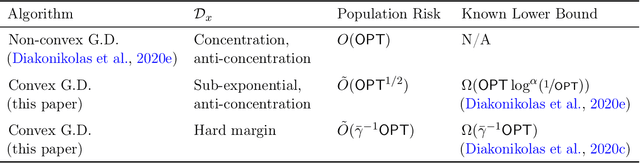
Abstract:We analyze the properties of gradient descent on convex surrogates for the zero-one loss for the agnostic learning of linear halfspaces. If $\mathsf{OPT}$ is the best classification error achieved by a halfspace, by appealing to the notion of soft margins we are able to show that gradient descent finds halfspaces with classification error $\tilde O(\mathsf{OPT}^{1/2}) + \varepsilon$ in $\mathrm{poly}(d,1/\varepsilon)$ time and sample complexity for a broad class of distributions that includes log-concave isotropic distributions as a subclass. Along the way we answer a question recently posed by Ji et al. (2020) on how the tail behavior of a loss function can affect sample complexity and runtime guarantees for gradient descent.
Provably Efficient Reinforcement Learning for Discounted MDPs with Feature Mapping
Jun 23, 2020
Abstract:Modern tasks in reinforcement learning are always with large state and action spaces. To deal with them efficiently, one often uses predefined feature mapping to represents states and actions in a low dimensional space. In this paper, we study reinforcement learning with feature mapping for discounted Markov Decision Processes (MDPs). We propose a novel algorithm which makes use of the feature mapping and obtains a $\tilde O(d\sqrt{T}/(1-\gamma)^2)$ regret, where $d$ is the dimension of the feature space, $T$ is the time horizon and $\gamma$ is the discount factor of the MDP. To the best of our knowledge, this is the first polynomial regret bound without accessing to a generative model or making strong assumptions such as ergodicity of the MDP. By constructing a special class of MDPs, we also show that for any algorithms, the regret is lower bounded by $\Omega(d\sqrt{T}/(1-\gamma)^{1.5})$. Our upper and lower bound results together suggest that the proposed reinforcement learning algorithm is near-optimal up to a $(1-\gamma)^{-0.5}$ factor.
RayS: A Ray Searching Method for Hard-label Adversarial Attack
Jun 23, 2020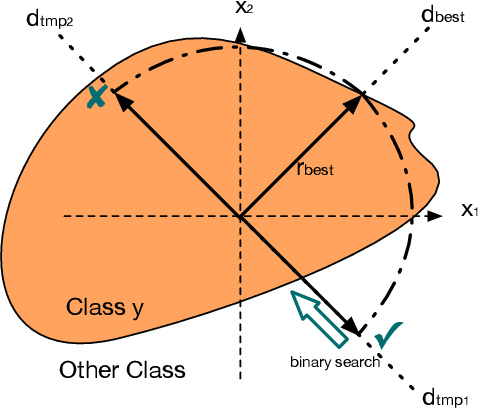
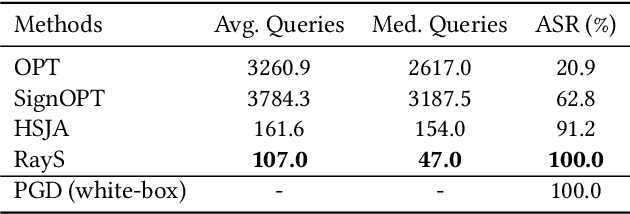

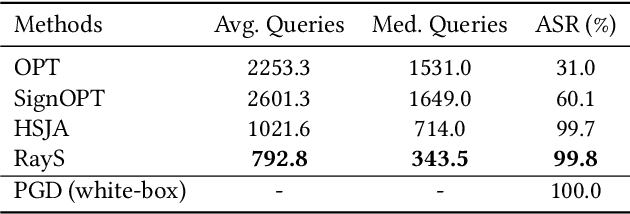
Abstract:Deep neural networks are vulnerable to adversarial attacks. Among different attack settings, the most challenging yet the most practical one is the hard-label setting where the attacker only has access to the hard-label output (prediction label) of the target model. Previous attempts are neither effective enough in terms of attack success rate nor efficient enough in terms of query complexity under the widely used $L_\infty$ norm threat model. In this paper, we present the Ray Searching attack (RayS), which greatly improves the hard-label attack effectiveness as well as efficiency. Unlike previous works, we reformulate the continuous problem of finding the closest decision boundary into a discrete problem that does not require any zeroth-order gradient estimation. In the meantime, all unnecessary searches are eliminated via a fast check step. This significantly reduces the number of queries needed for our hard-label attack. Moreover, interestingly, we found that the proposed RayS attack can also be used as a sanity check for possible "falsely robust" models. On several recently proposed defenses that claim to achieve the state-of-the-art robust accuracy, our attack method demonstrates that the current white-box/black-box attacks could still give a false sense of security and the robust accuracy drop between the most popular PGD attack and RayS attack could be as large as $28\%$. We believe that our proposed RayS attack could help identify falsely robust models that beat most white-box/black-box attacks.
Revisiting Membership Inference Under Realistic Assumptions
Jun 21, 2020
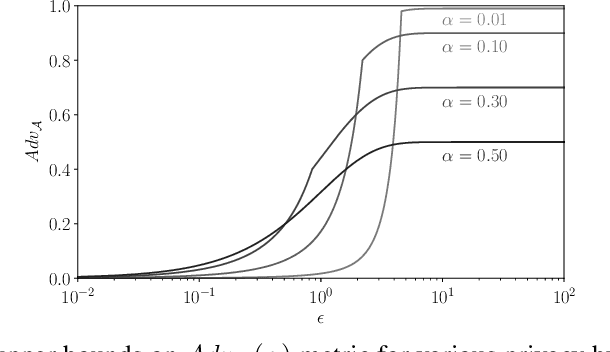
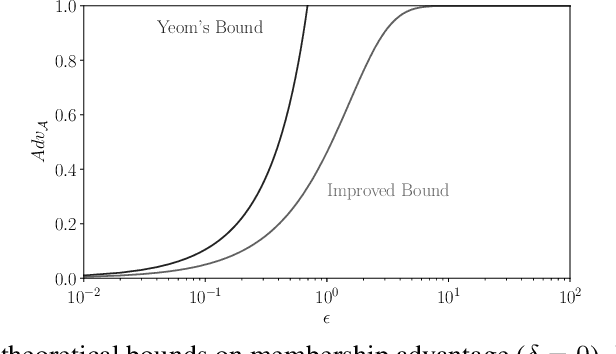

Abstract:Membership inference attacks on models trained using machine learning have been shown to pose significant privacy risks. However, previous works on membership inference assume a balanced prior distribution where the adversary randomly chooses target records from a pool that has equal numbers of members and non-members. Such an assumption of balanced prior is unrealistic in practical scenarios. This paper studies membership inference attacks under more realistic assumptions. First, we consider skewed priors where a non-member is more likely to occur than a member record. For this, we use metric based on positive predictive value (PPV) in conjunction with membership advantage for privacy leakage evaluation, since PPV considers the prior. Second, we consider adversaries that can select inference thresholds according to their attack goals. For this, we develop a threshold selection procedure that improves inference attacks. We also propose a new membership inference attack called Merlin which outperforms previous attacks. Our experimental evaluation shows that while models trained without privacy mechanisms are vulnerable to membership inference attacks in balanced prior settings, there appears to be negligible privacy risk in the skewed prior setting. Code for our experiments can be found here: https://github.com/bargavj/EvaluatingDPML.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge