Sharpness-Aware Minimization and the Edge of Stability

Recent experiments have shown that, often, when training a neural network with gradient descent (GD) with a step size $\eta$, the operator norm of the Hessian of the loss grows until it approximately reaches $2/\eta$, after which it fluctuates around this value. The quantity $2/\eta$ has been called the "edge of stability" based on consideration of a local quadratic approximation of the loss. We perform a similar calculation to arrive at an "edge of stability" for Sharpness-Aware Minimization (SAM), a variant of GD which has been shown to improve its generalization. Unlike the case for GD, the resulting SAM-edge depends on the norm of the gradient. Using three deep learning training tasks, we see empirically that SAM operates on the edge of stability identified by this analysis.

Prediction, Learning, Uniform Convergence, and Scale-sensitive Dimensions

We present a new general-purpose algorithm for learning classes of $[0,1]$-valued functions in a generalization of the prediction model, and prove a general upper bound on the expected absolute error of this algorithm in terms of a scale-sensitive generalization of the Vapnik dimension proposed by Alon, Ben-David, Cesa-Bianchi and Haussler. We give lower bounds implying that our upper bounds cannot be improved by more than a constant factor in general. We apply this result, together with techniques due to Haussler and to Benedek and Itai, to obtain new upper bounds on packing numbers in terms of this scale-sensitive notion of dimension. Using a different technique, we obtain new bounds on packing numbers in terms of Kearns and Schapire's fat-shattering function. We show how to apply both packing bounds to obtain improved general bounds on the sample complexity of agnostic learning. For each $\epsilon > 0$, we establish weaker sufficient and stronger necessary conditions for a class of $[0,1]$-valued functions to be agnostically learnable to within $\epsilon$, and to be an $\epsilon$-uniform Glivenko-Cantelli class. This is a manuscript that was accepted by JCSS, together with a correction.

The Dynamics of Sharpness-Aware Minimization: Bouncing Across Ravines and Drifting Towards Wide Minima

We consider Sharpness-Aware Minimization (SAM), a gradient-based optimization method for deep networks that has exhibited performance improvements on image and language prediction problems. We show that when SAM is applied with a convex quadratic objective, for most random initializations it converges to a cycle that oscillates between either side of the minimum in the direction with the largest curvature, and we provide bounds on the rate of convergence. In the non-quadratic case, we show that such oscillations effectively perform gradient descent, with a smaller step-size, on the spectral norm of the Hessian. In such cases, SAM's update may be regarded as a third derivative -- the derivative of the Hessian in the leading eigenvector direction -- that encourages drift toward wider minima.

Deep Linear Networks can Benignly Overfit when Shallow Ones Do

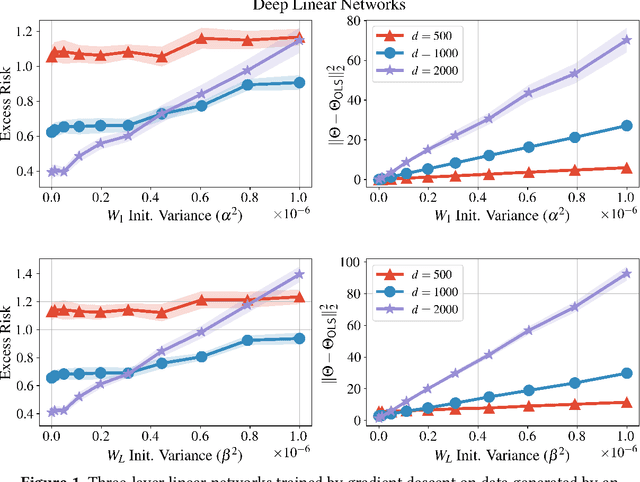
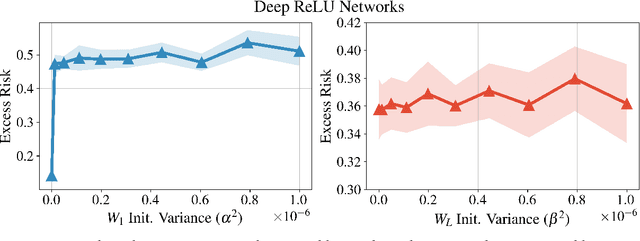
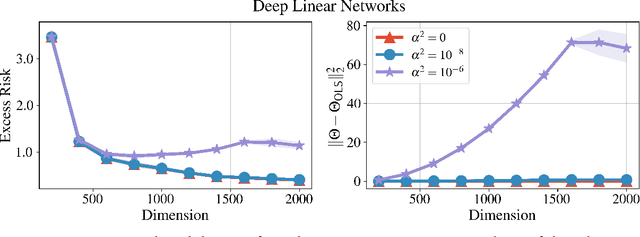
We bound the excess risk of interpolating deep linear networks trained using gradient flow. In a setting previously used to establish risk bounds for the minimum $\ell_2$-norm interpolant, we show that randomly initialized deep linear networks can closely approximate or even match known bounds for the minimum $\ell_2$-norm interpolant. Our analysis also reveals that interpolating deep linear models have exactly the same conditional variance as the minimum $\ell_2$-norm solution. Since the noise affects the excess risk only through the conditional variance, this implies that depth does not improve the algorithm's ability to "hide the noise". Our simulations verify that aspects of our bounds reflect typical behavior for simple data distributions. We also find that similar phenomena are seen in simulations with ReLU networks, although the situation there is more nuanced.

The perils of being unhinged: On the accuracy of classifiers minimizing a noise-robust convex loss

van Rooyen et al. introduced a notion of convex loss functions being robust to random classification noise, and established that the "unhinged" loss function is robust in this sense. In this note we study the accuracy of binary classifiers obtained by minimizing the unhinged loss, and observe that even for simple linearly separable data distributions, minimizing the unhinged loss may only yield a binary classifier with accuracy no better than random guessing.

Foolish Crowds Support Benign Overfitting

We prove a lower bound on the excess risk of sparse interpolating procedures for linear regression with Gaussian data in the overparameterized regime. We apply this result to obtain a lower bound for basis pursuit (the minimum $\ell_1$-norm interpolant) that implies that its excess risk can converge at an exponentially slower rate than OLS (the minimum $\ell_2$-norm interpolant), even when the ground truth is sparse. Our analysis exposes the benefit of an effect analogous to the "wisdom of the crowd", except here the harm arising from fitting the noise is ameliorated by spreading it among many directions - the variance reduction arises from a foolish crowd.

The Interplay Between Implicit Bias and Benign Overfitting in Two-Layer Linear Networks

The recent success of neural network models has shone light on a rather surprising statistical phenomenon: statistical models that perfectly fit noisy data can generalize well to unseen test data. Understanding this phenomenon of $\textit{benign overfitting}$ has attracted intense theoretical and empirical study. In this paper, we consider interpolating two-layer linear neural networks trained with gradient flow on the squared loss and derive bounds on the excess risk when the covariates satisfy sub-Gaussianity and anti-concentration properties, and the noise is independent and sub-Gaussian. By leveraging recent results that characterize the implicit bias of this estimator, our bounds emphasize the role of both the quality of the initialization as well as the properties of the data covariance matrix in achieving low excess risk.

Properties of the After Kernel

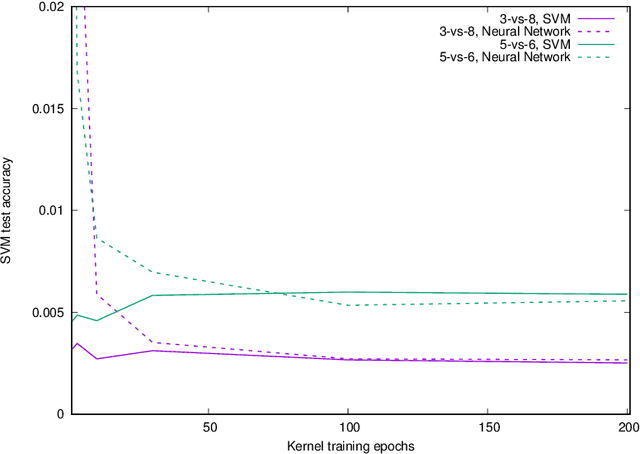
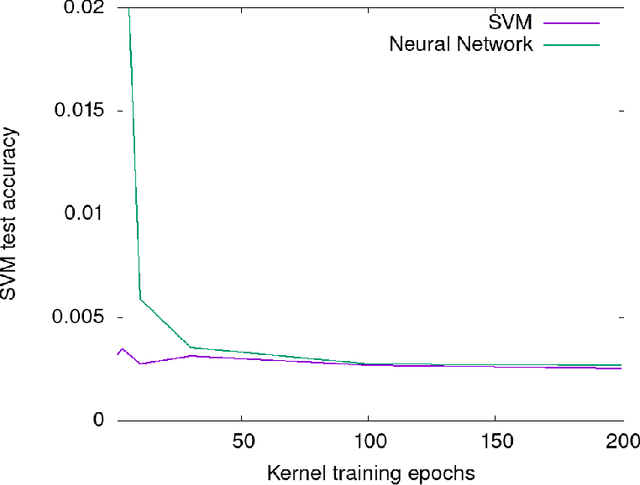
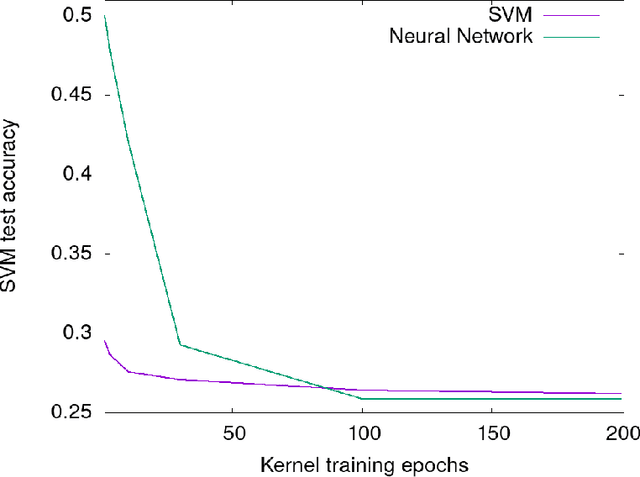
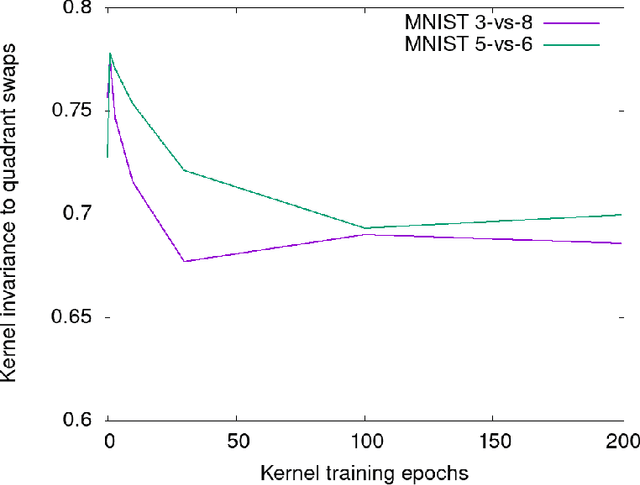
The Neural Tangent Kernel (NTK) is the wide-network limit of a kernel defined using neural networks at initialization, whose embedding is the gradient of the output of the network with respect to its parameters. We study the "after kernel", which is defined using the same embedding, except after training, for neural networks with standard architectures, on binary classification problems extracted from MNIST and CIFAR-10, trained using SGD in a standard way. For some dataset-architecture pairs, after a few epochs of neural network training, a hard-margin SVM using the network's after kernel is much more accurate than when the network's initial kernel is used. For networks with an architecture similar to VGG, the after kernel is more "global", in the sense that it is less invariant to transformations of input images that disrupt the global structure of the image while leaving the local statistics largely intact. For fully connected networks, the after kernel is less global in this sense. The after kernel tends to be more invariant to small shifts, rotations and zooms; data augmentation does not improve these invariances. The (finite approximation to the) conjugate kernel, obtained using the last layer of hidden nodes, sometimes, but not always, provides a good approximation to the NTK and the after kernel.

When does gradient descent with logistic loss interpolate using deep networks with smoothed ReLU activations?

We establish conditions under which gradient descent applied to fixed-width deep networks drives the logistic loss to zero, and prove bounds on the rate of convergence. Our analysis applies for smoothed approximations to the ReLU, such as Swish and the Huberized ReLU, proposed in previous applied work. We provide two sufficient conditions for convergence. The first is simply a bound on the loss at initialization. The second is a data separation condition used in prior analyses.

When does gradient descent with logistic loss find interpolating two-layer networks?

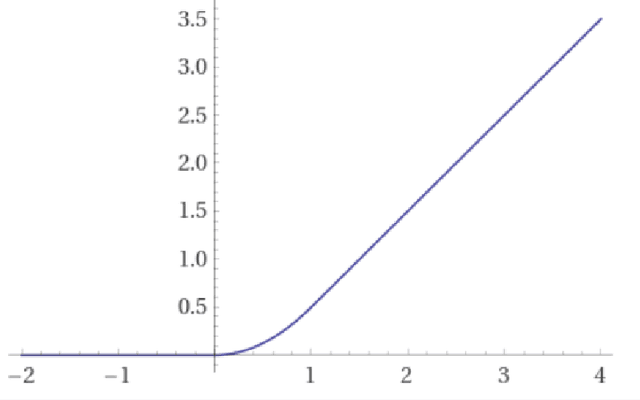
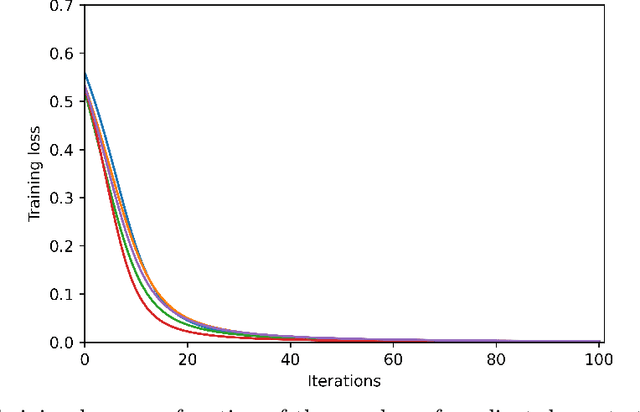
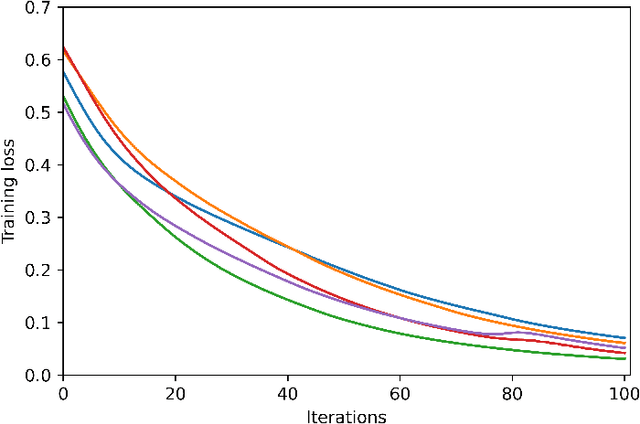
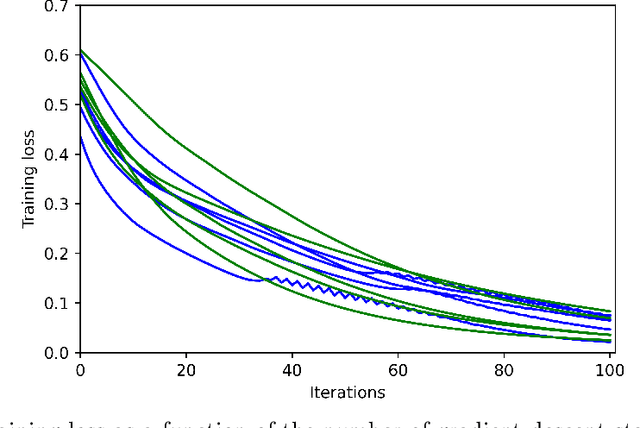
We study the training of finite-width two-layer smoothed ReLU networks for binary classification using the logistic loss. We show that gradient descent drives the training loss to zero if the initial loss is small enough. When the data satisfies certain cluster and separation conditions and the network is wide enough, we show that one step of gradient descent reduces the loss sufficiently that the first result applies. In contrast, all past analyses of fixed-width networks that we know do not guarantee that the training loss goes to zero.