Sentient Agent as a Judge: Evaluating Higher-Order Social Cognition in Large Language Models

Assessing how well a large language model (LLM) understands human, rather than merely text, remains an open challenge. To bridge the gap, we introduce Sentient Agent as a Judge (SAGE), an automated evaluation framework that measures an LLM's higher-order social cognition. SAGE instantiates a Sentient Agent that simulates human-like emotional changes and inner thoughts during interaction, providing a more realistic evaluation of the tested model in multi-turn conversations. At every turn, the agent reasons about (i) how its emotion changes, (ii) how it feels, and (iii) how it should reply, yielding a numerical emotion trajectory and interpretable inner thoughts. Experiments on 100 supportive-dialogue scenarios show that the final Sentient emotion score correlates strongly with Barrett-Lennard Relationship Inventory (BLRI) ratings and utterance-level empathy metrics, validating psychological fidelity. We also build a public Sentient Leaderboard covering 18 commercial and open-source models that uncovers substantial gaps (up to 4x) between frontier systems (GPT-4o-Latest, Gemini2.5-Pro) and earlier baselines, gaps not reflected in conventional leaderboards (e.g., Arena). SAGE thus provides a principled, scalable and interpretable tool for tracking progress toward genuinely empathetic and socially adept language agents.

Equivariant Manifold Flows

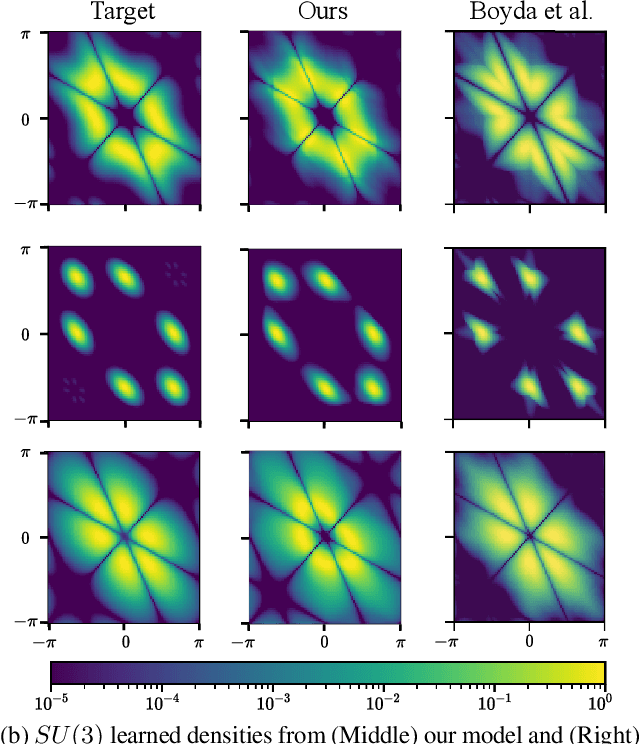
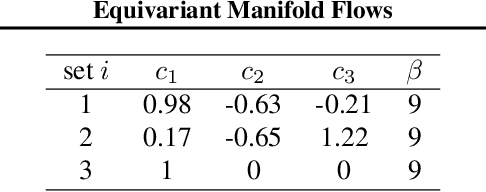
Tractably modelling distributions over manifolds has long been an important goal in the natural sciences. Recent work has focused on developing general machine learning models to learn such distributions. However, for many applications these distributions must respect manifold symmetries -- a trait which most previous models disregard. In this paper, we lay the theoretical foundations for learning symmetry-invariant distributions on arbitrary manifolds via equivariant manifold flows. We demonstrate the utility of our approach by using it to learn gauge invariant densities over $SU(n)$ in the context of quantum field theory.

Neural Manifold Ordinary Differential Equations

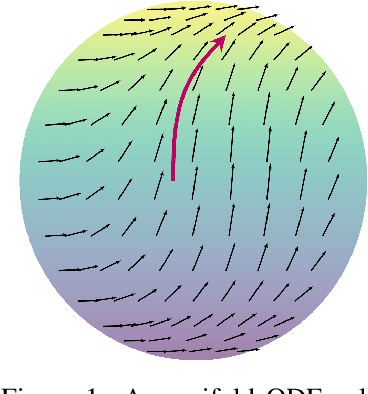
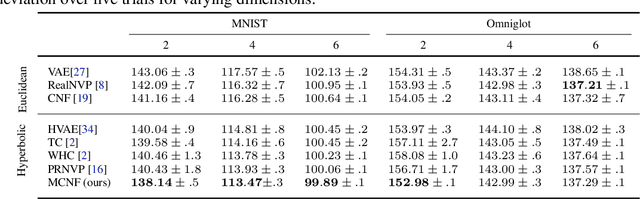
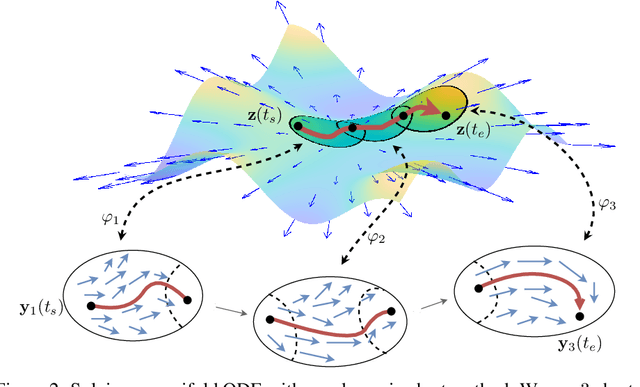
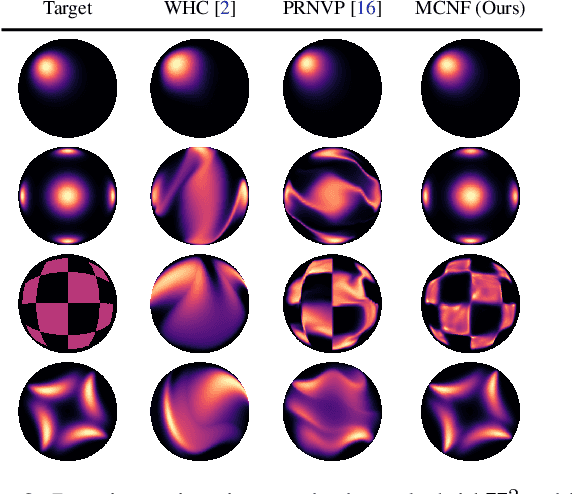
To better conform to data geometry, recent deep generative modelling techniques adapt Euclidean constructions to non-Euclidean spaces. In this paper, we study normalizing flows on manifolds. Previous work has developed flow models for specific cases; however, these advancements hand craft layers on a manifold-by-manifold basis, restricting generality and inducing cumbersome design constraints. We overcome these issues by introducing Neural Manifold Ordinary Differential Equations, a manifold generalization of Neural ODEs, which enables the construction of Manifold Continuous Normalizing Flows (MCNFs). MCNFs require only local geometry (therefore generalizing to arbitrary manifolds) and compute probabilities with continuous change of variables (allowing for a simple and expressive flow construction). We find that leveraging continuous manifold dynamics produces a marked improvement for both density estimation and downstream tasks.

Differentiating through the Fréchet Mean

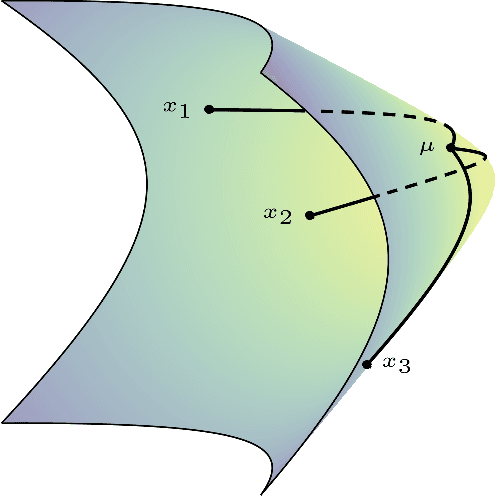
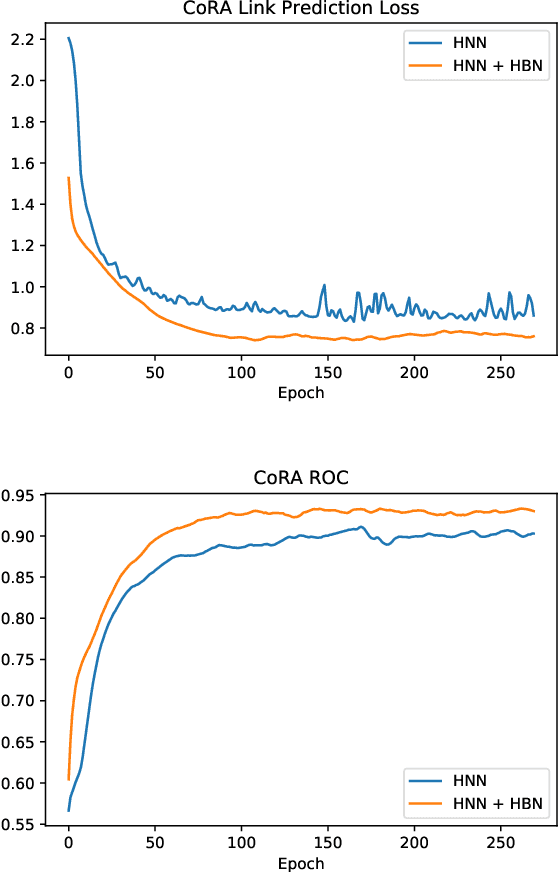
Recent advances in deep representation learning on Riemannian manifolds extend classical deep learning operations to better capture the geometry of the manifold. One possible extension is the Fr\'echet mean, the generalization of the Euclidean mean; however, it has been difficult to apply because it lacks a closed form with an easily computable derivative. In this paper, we show how to differentiate through the Fr\'echet mean for arbitrary Riemannian manifolds. Then, focusing on hyperbolic space, we derive explicit gradient expressions and a fast, accurate, and hyperparameter-free Fr\'echet mean solver. This fully integrates the Fr\'echet mean into the hyperbolic neural network pipeline. To demonstrate this integration, we present two case studies. First, we apply our Fr\'echet mean to the existing Hyperbolic Graph Convolutional Network, replacing its projected aggregation to obtain state-of-the-art results on datasets with high hyperbolicity. Second, to demonstrate the Fr\'echet mean's capacity to generalize Euclidean neural network operations, we develop a hyperbolic batch normalization method that gives an improvement parallel to the one observed in the Euclidean setting.

Adversarial Example Decomposition

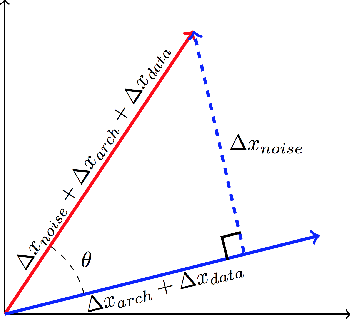
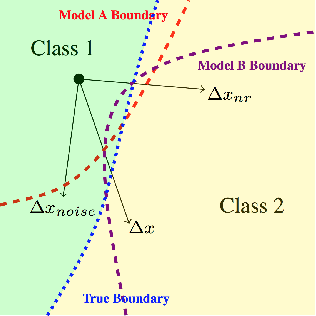
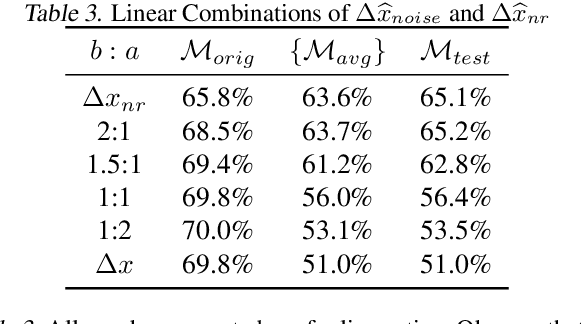
Research has shown that widely used deep neural networks are vulnerable to carefully crafted adversarial perturbations. Moreover, these adversarial perturbations often transfer across models. We hypothesize that adversarial weakness is composed of three sources of bias: architecture, dataset, and random initialization. We show that one can decompose adversarial examples into an architecture-dependent component, data-dependent component, and noise-dependent component and that these components behave intuitively. For example, noise-dependent components transfer poorly to all other models, while architecture-dependent components transfer better to retrained models with the same architecture. In addition, we demonstrate that these components can be recombined to improve transferability without sacrificing efficacy on the original model.