Defence against adversarial attacks using classical and quantum-enhanced Boltzmann machines

We provide a robust defence to adversarial attacks on discriminative algorithms. Neural networks are naturally vulnerable to small, tailored perturbations in the input data that lead to wrong predictions. On the contrary, generative models attempt to learn the distribution underlying a dataset, making them inherently more robust to small perturbations. We use Boltzmann machines for discrimination purposes as attack-resistant classifiers, and compare them against standard state-of-the-art adversarial defences. We find improvements ranging from 5% to 72% against attacks with Boltzmann machines on the MNIST dataset. We furthermore complement the training with quantum-enhanced sampling from the D-Wave 2000Q annealer, finding results comparable with classical techniques and with marginal improvements in some cases. These results underline the relevance of probabilistic methods in constructing neural networks and demonstrate the power of quantum computers, even with limited hardware capabilities. This work is dedicated to the memory of Peter Wittek.

An Artificial Spiking Quantum Neuron

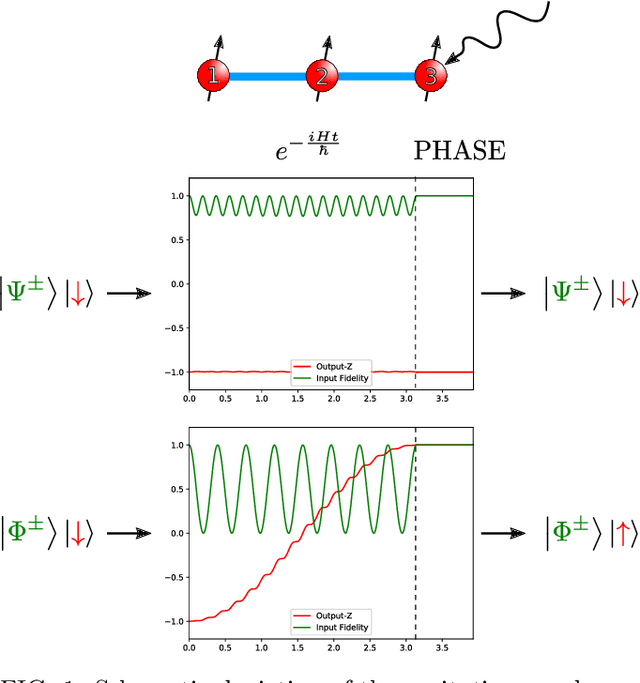
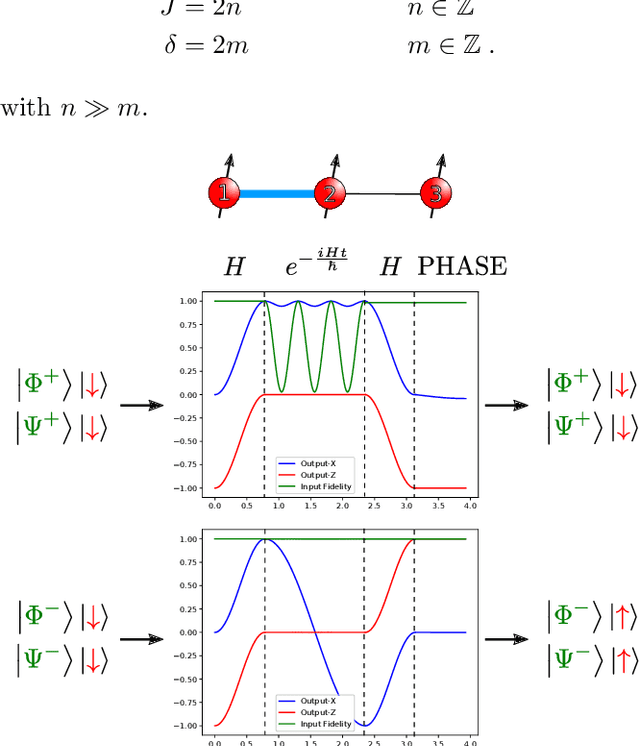
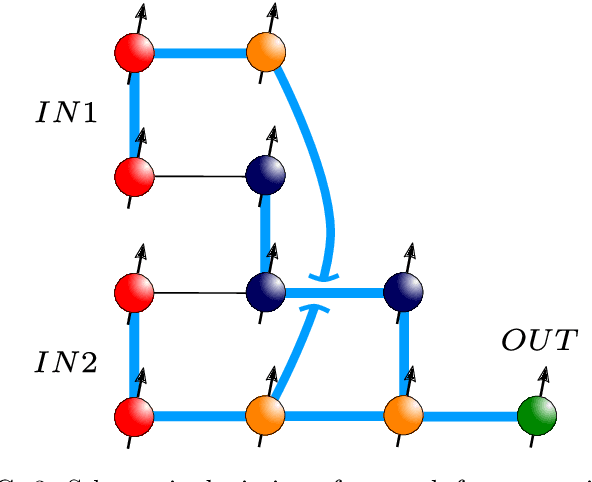
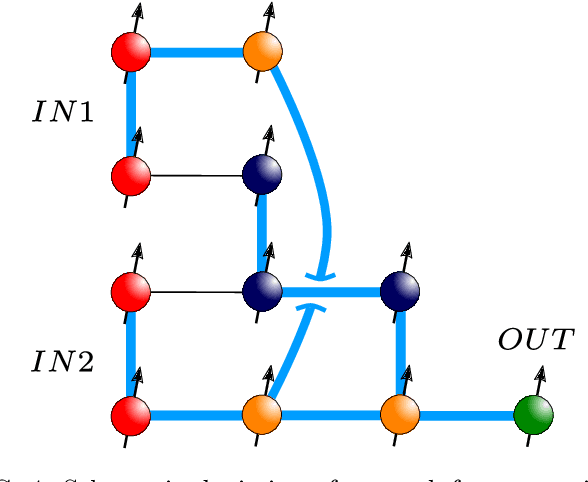
Artificial spiking neural networks have found applications in areas where the temporal nature of activation offers an advantage, such as time series prediction and signal processing. To improve their efficiency, spiking architectures often run on custom-designed neuromorphic hardware, but, despite their attractive properties, these implementations have been limited to digital systems. We describe an artificial quantum spiking neuron that relies on the dynamical evolution of two easy to implement Hamiltonians and subsequent local measurements. The architecture allows exploiting complex amplitudes and back-action from measurements to influence the input. This approach to learning protocols is advantageous in the case where the input and output of the system are both quantum states. We demonstrate this through the classification of Bell pairs which can be seen as a certification protocol. Stacking the introduced elementary building blocks into larger networks combines the spatiotemporal features of a spiking neural network with the non-local quantum correlations across the graph.

Machine Learning by Two-Dimensional Hierarchical Tensor Networks: A Quantum Information Theoretic Perspective on Deep Architectures

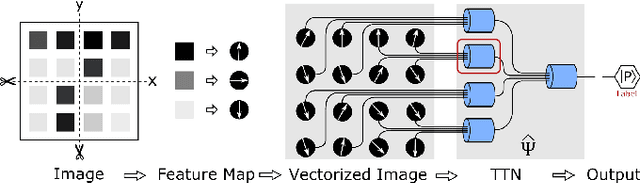
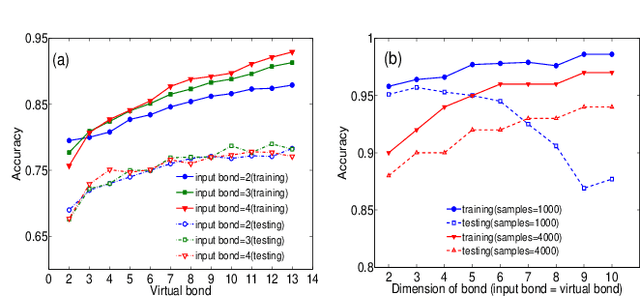
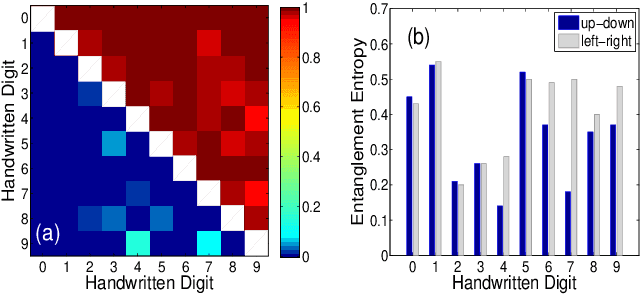
The resemblance between the methods used in quantum-many body physics and in machine learning has drawn considerable attention. In particular, tensor networks (TNs) and deep learning architectures bear striking similarities to the extent that TNs can be used for machine learning. Previous results used one-dimensional TNs in image recognition, showing limited scalability and flexibilities. In this work, we train two-dimensional hierarchical TNs to solve image recognition problems, using a training algorithm derived from the multipartite entanglement renormalization ansatz. This approach introduces novel mathematical connections among quantum many-body physics, quantum information theory, and machine learning. While keeping the TN unitary in the training phase, TN states are defined, which optimally encode classes of images into quantum many-body states. We study the quantum features of the TN states, including quantum entanglement and fidelity. We find these quantities could be novel properties that characterize the image classes, as well as the machine learning tasks. Our work could contribute to the research on identifying/modeling quantum artificial intelligences.

Bayesian Deep Learning on a Quantum Computer

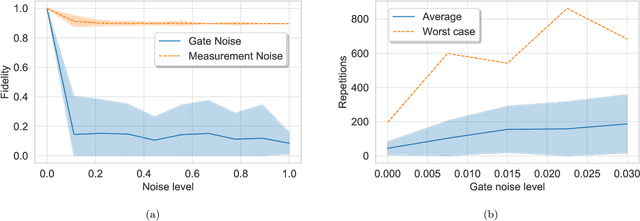
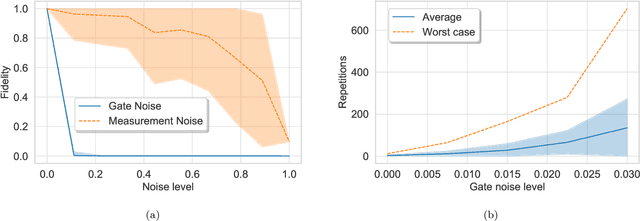
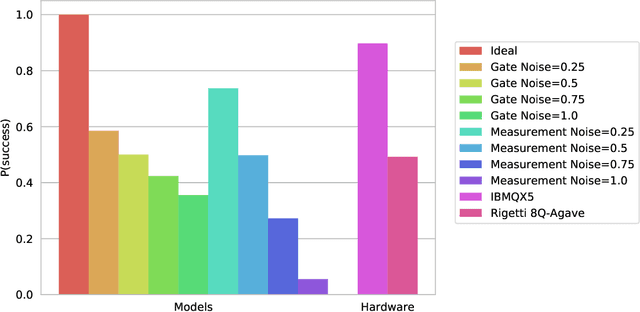
Bayesian methods in machine learning, such as Gaussian processes, have great advantages compared to other techniques. In particular, they provide estimates of the uncertainty associated with a prediction. Extending the Bayesian approach to deep architectures has remained a major challenge. Recent results connected deep feedforward neural networks with Gaussian processes, allowing training without backpropagation. This connection enables us to leverage a quantum algorithm designed for Gaussian processes and develop a new algorithm for Bayesian deep learning on quantum computers. The properties of the kernel matrix in the Gaussian process ensure the efficient execution of the core component of the protocol, quantum matrix inversion, providing an at least polynomial speedup over the classical algorithm. Furthermore, we demonstrate the execution of the algorithm on contemporary quantum computers and analyze its robustness with respect to realistic noise models.

Quantum Machine Learning

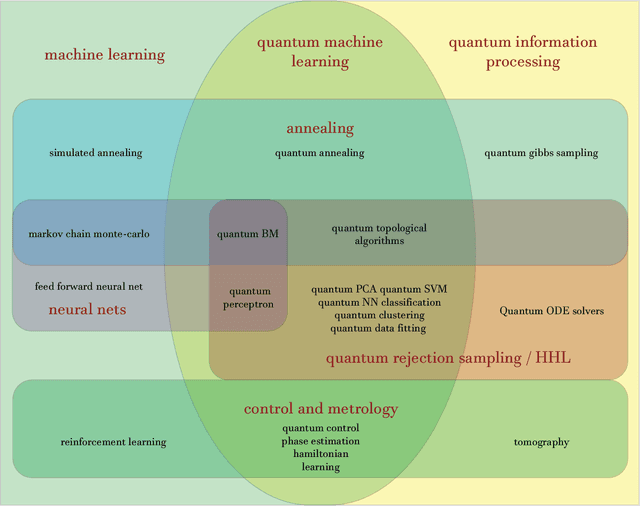
Fuelled by increasing computer power and algorithmic advances, machine learning techniques have become powerful tools for finding patterns in data. Since quantum systems produce counter-intuitive patterns believed not to be efficiently produced by classical systems, it is reasonable to postulate that quantum computers may outperform classical computers on machine learning tasks. The field of quantum machine learning explores how to devise and implement concrete quantum software that offers such advantages. Recent work has made clear that the hardware and software challenges are still considerable but has also opened paths towards solutions.

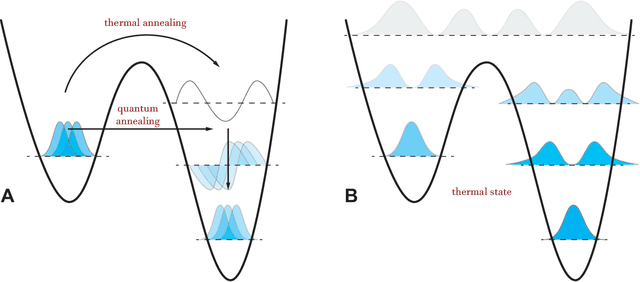
Identifying Quantum Phase Transitions with Adversarial Neural Networks

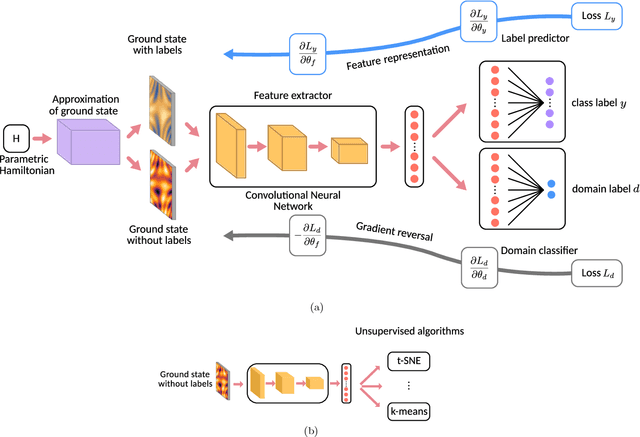
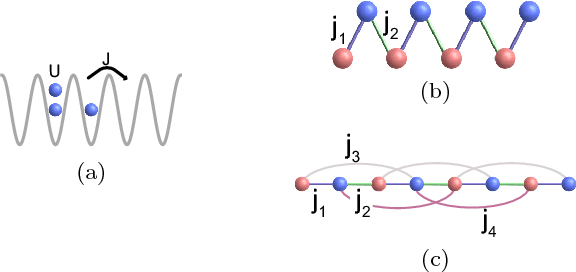
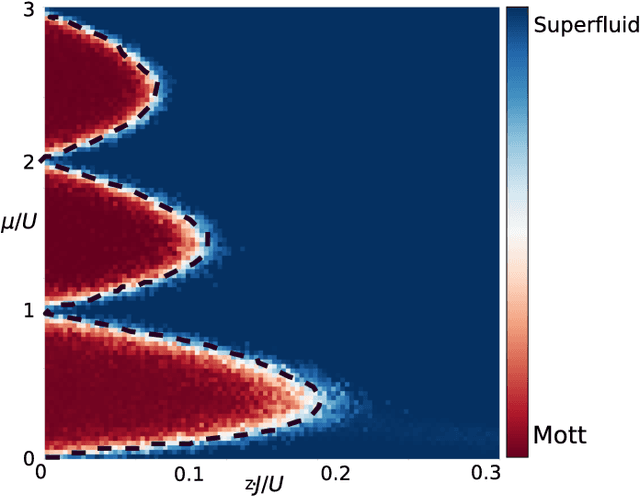
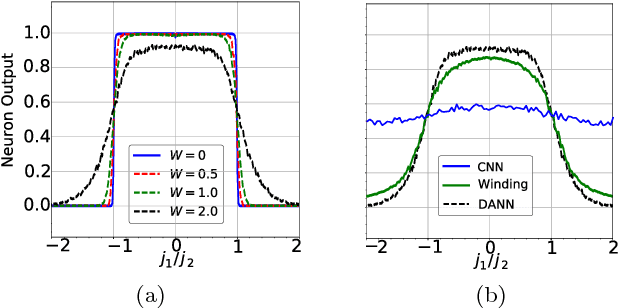
The identification of phases of matter is a challenging task, especially in quantum mechanics, where the complexity of the ground state appears to grow exponentially with the size of the system. We address this problem with state-of-the-art deep learning techniques: adversarial domain adaptation. We derive the phase diagram of the whole parameter space starting from a fixed and known subspace using unsupervised learning. The input data set contains both labeled and unlabeled data instances. The first kind is a system that admits an accurate analytical or numerical solution, and one can recover its phase diagram. The second type is the physical system with an unknown phase diagram. Adversarial domain adaptation uses both types of data to create invariant feature extracting layers in a deep learning architecture. Once these layers are trained, we can attach an unsupervised learner to the network to find phase transitions. We show the success of this technique by applying it on several paradigmatic models: the Ising model with different temperatures, the Bose-Hubbard model, and the SSH model with disorder. The input is the ground state without any manual feature engineering, and the dimension of the parameter space is unrestricted. The method finds unknown transitions successfully and predicts transition points in close agreement with standard methods. This study opens the door to the classification of physical systems where the phases boundaries are complex such as the many-body localization problem or the Bose glass phase.

Somoclu: An Efficient Parallel Library for Self-Organizing Maps

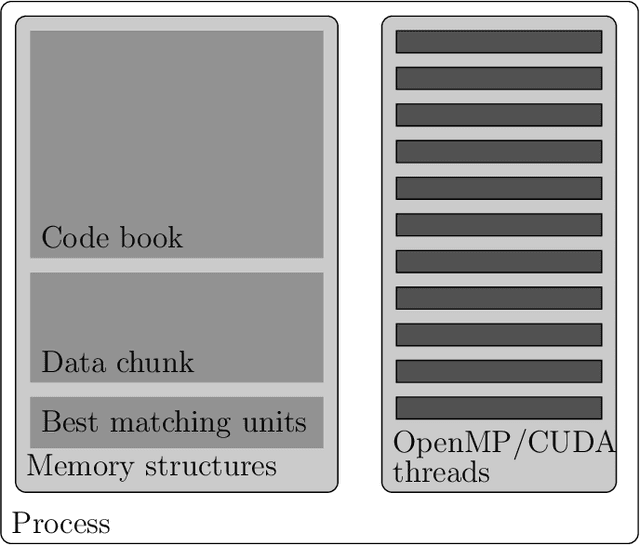
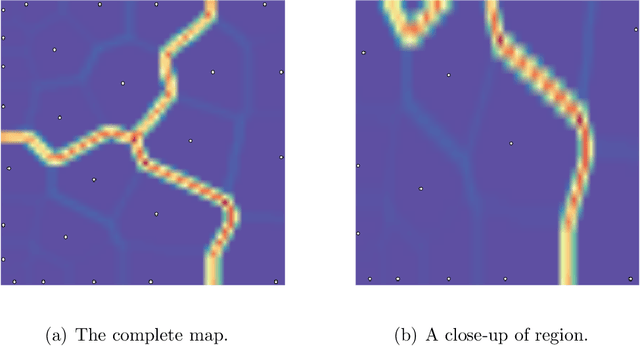
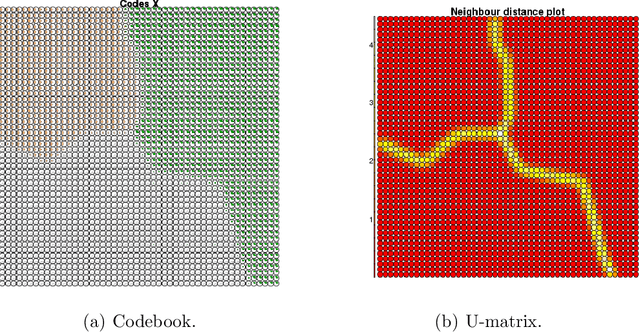
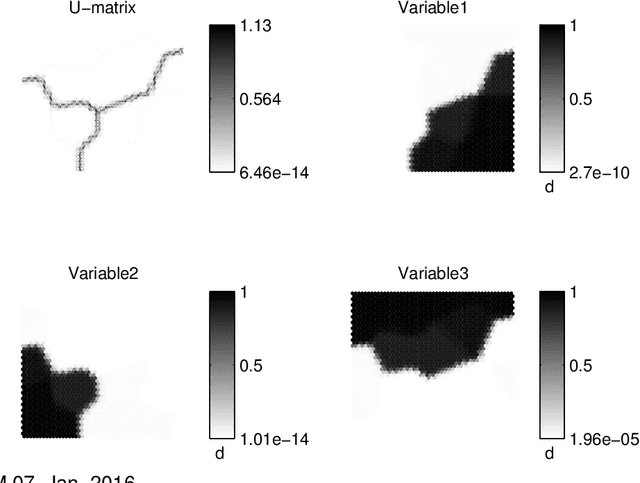
Somoclu is a massively parallel tool for training self-organizing maps on large data sets written in C++. It builds on OpenMP for multicore execution, and on MPI for distributing the workload across the nodes in a cluster. It is also able to boost training by using CUDA if graphics processing units are available. A sparse kernel is included, which is useful for high-dimensional but sparse data, such as the vector spaces common in text mining workflows. Python, R and MATLAB interfaces facilitate interactive use. Apart from fast execution, memory use is highly optimized, enabling training large emergent maps even on a single computer.

Inductive supervised quantum learning

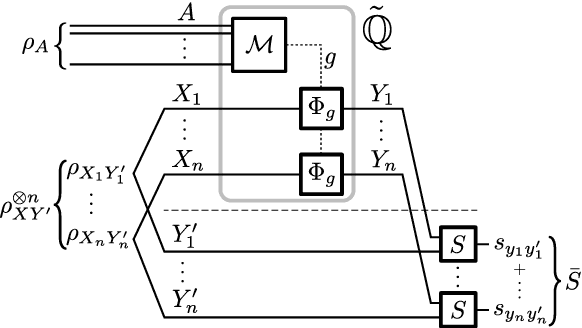
In supervised learning, an inductive learning algorithm extracts general rules from observed training instances, then the rules are applied to test instances. We show that this splitting of training and application arises naturally, in the classical setting, from a simple independence requirement with a physical interpretation of being non-signalling. Thus, two seemingly different definitions of inductive learning happen to coincide. This follows from the properties of classical information that break down in the quantum setup. We prove a quantum de Finetti theorem for quantum channels, which shows that in the quantum case, the equivalence holds in the asymptotic setting, that is, for large number of test instances. This reveals a natural analogy between classical learning protocols and their quantum counterparts, justifying a similar treatment, and allowing to inquire about standard elements in computational learning theory, such as structural risk minimization and sample complexity.

Learning in Quantum Control: High-Dimensional Global Optimization for Noisy Quantum Dynamics

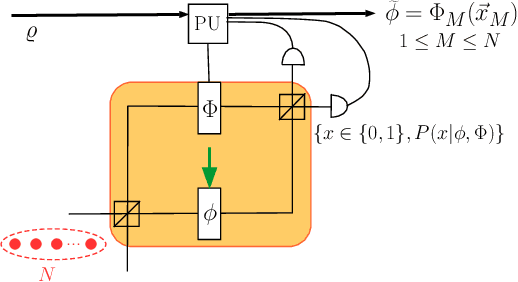
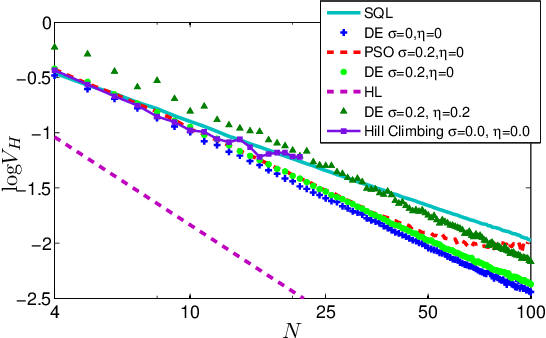
Quantum control is valuable for various quantum technologies such as high-fidelity gates for universal quantum computing, adaptive quantum-enhanced metrology, and ultra-cold atom manipulation. Although supervised machine learning and reinforcement learning are widely used for optimizing control parameters in classical systems, quantum control for parameter optimization is mainly pursued via gradient-based greedy algorithms. Although the quantum fitness landscape is often compatible with greedy algorithms, sometimes greedy algorithms yield poor results, especially for large-dimensional quantum systems. We employ differential evolution algorithms to circumvent the stagnation problem of non-convex optimization. We improve quantum control fidelity for noisy system by averaging over the objective function. To reduce computational cost, we introduce heuristics for early termination of runs and for adaptive selection of search subspaces. Our implementation is massively parallel and vectorized to reduce run time even further. We demonstrate our methods with two examples, namely quantum phase estimation and quantum gate design, for which we achieve superior fidelity and scalability than obtained using greedy algorithms.

Quantum Enhanced Inference in Markov Logic Networks

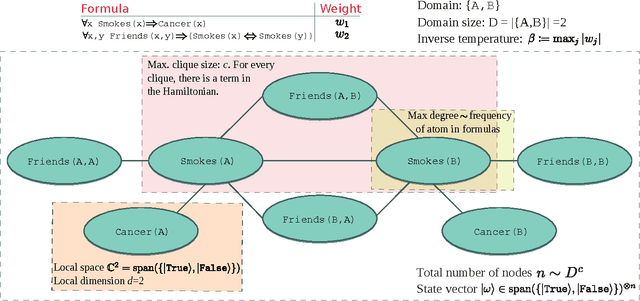
Markov logic networks (MLNs) reconcile two opposing schools in machine learning and artificial intelligence: causal networks, which account for uncertainty extremely well, and first-order logic, which allows for formal deduction. An MLN is essentially a first-order logic template to generate Markov networks. Inference in MLNs is probabilistic and it is often performed by approximate methods such as Markov chain Monte Carlo (MCMC) Gibbs sampling. An MLN has many regular, symmetric structures that can be exploited at both first-order level and in the generated Markov network. We analyze the graph structures that are produced by various lifting methods and investigate the extent to which quantum protocols can be used to speed up Gibbs sampling with state preparation and measurement schemes. We review different such approaches, discuss their advantages, theoretical limitations, and their appeal to implementations. We find that a straightforward application of a recent result yields exponential speedup compared to classical heuristics in approximate probabilistic inference, thereby demonstrating another example where advanced quantum resources can potentially prove useful in machine learning.