Quantum diffusion map for nonlinear dimensionality reduction

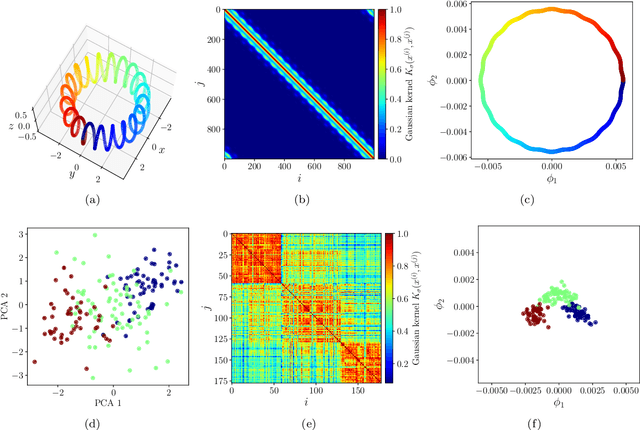
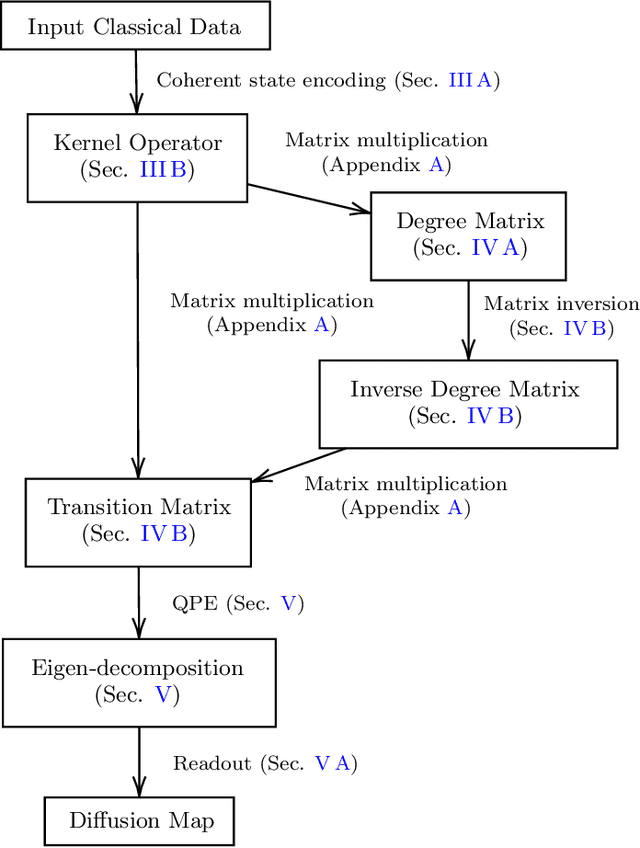
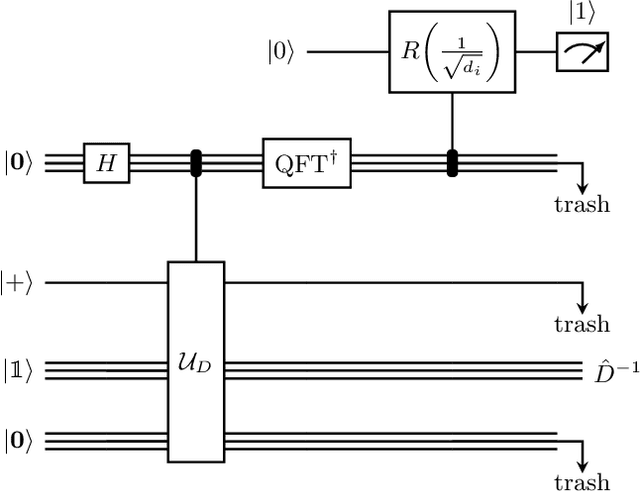
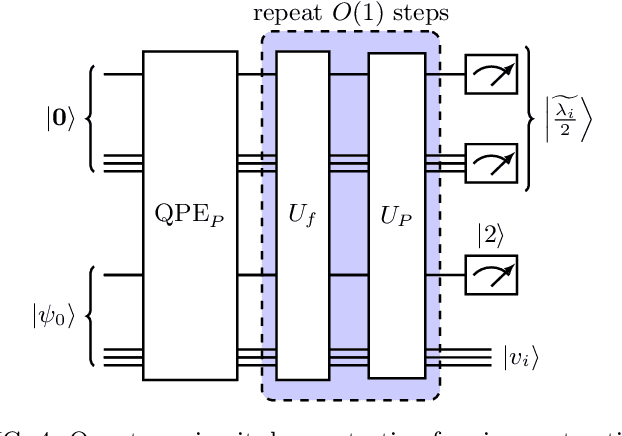
Inspired by random walk on graphs, diffusion map (DM) is a class of unsupervised machine learning that offers automatic identification of low-dimensional data structure hidden in a high-dimensional dataset. In recent years, among its many applications, DM has been successfully applied to discover relevant order parameters in many-body systems, enabling automatic classification of quantum phases of matter. However, classical DM algorithm is computationally prohibitive for a large dataset, and any reduction of the time complexity would be desirable. With a quantum computational speedup in mind, we propose a quantum algorithm for DM, termed quantum diffusion map (qDM). Our qDM takes as an input N classical data vectors, performs an eigen-decomposition of the Markov transition matrix in time $O(\log^3 N)$, and classically constructs the diffusion map via the readout (tomography) of the eigenvectors, giving a total runtime of $O(N^2 \text{polylog}\, N)$. Lastly, quantum subroutines in qDM for constructing a Markov transition operator, and for analyzing its spectral properties can also be useful for other random walk-based algorithms.

Robustness of Adaptive Quantum-Enhanced Phase Estimation

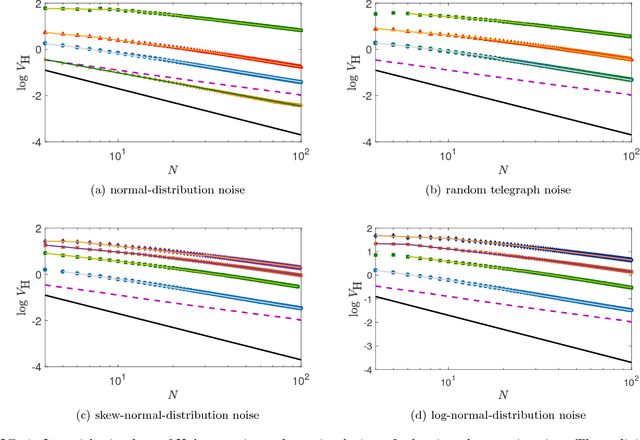
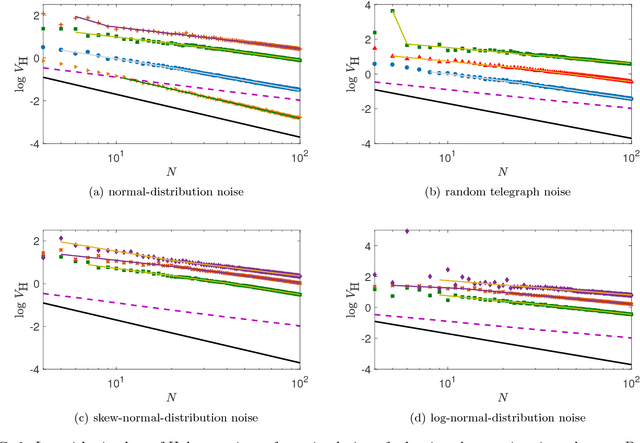
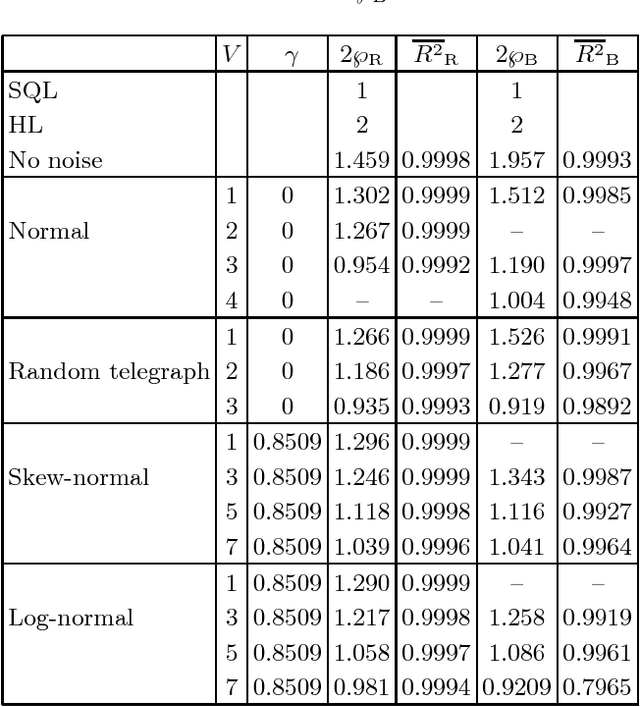
As all physical adaptive quantum-enhanced metrology schemes operate under noisy conditions with only partially understood noise characteristics, so a practical control policy must be robust even for unknown noise. We aim to devise a test to evaluate the robustness of AQEM policies and assess the resource used by the policies. The robustness test is performed on adaptive phase estimation by simulating the scheme under four phase noise models corresponding to the normal-distribution noise, the random telegraph noise, the skew-normal-distribution noise, and the log-normal-distribution noise. The control policies are devised either by a reinforcement-learning algorithm in the same noise condition, albeit ignorant of its properties, or a Bayesian-based feedback method that assumes no noise. Our robustness test and resource comparison can be used to determining the efficacy and selecting a suitable policy.

Learning in Quantum Control: High-Dimensional Global Optimization for Noisy Quantum Dynamics

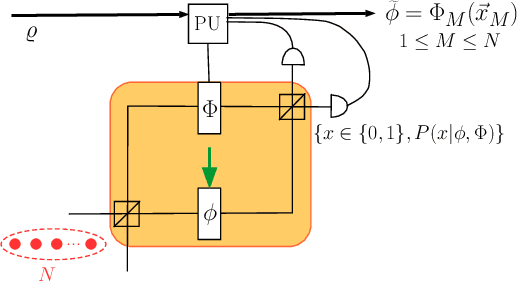
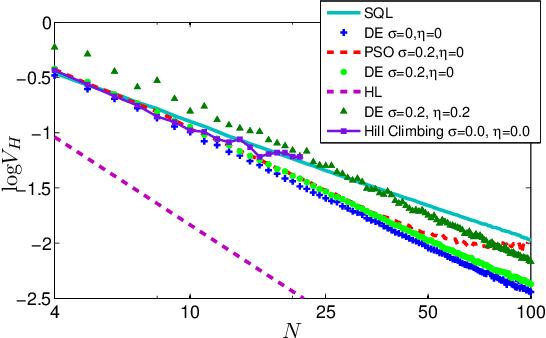
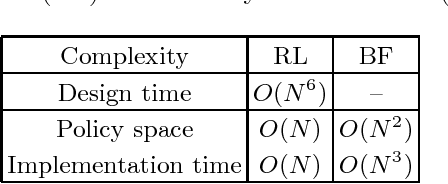
Quantum control is valuable for various quantum technologies such as high-fidelity gates for universal quantum computing, adaptive quantum-enhanced metrology, and ultra-cold atom manipulation. Although supervised machine learning and reinforcement learning are widely used for optimizing control parameters in classical systems, quantum control for parameter optimization is mainly pursued via gradient-based greedy algorithms. Although the quantum fitness landscape is often compatible with greedy algorithms, sometimes greedy algorithms yield poor results, especially for large-dimensional quantum systems. We employ differential evolution algorithms to circumvent the stagnation problem of non-convex optimization. We improve quantum control fidelity for noisy system by averaging over the objective function. To reduce computational cost, we introduce heuristics for early termination of runs and for adaptive selection of search subspaces. Our implementation is massively parallel and vectorized to reduce run time even further. We demonstrate our methods with two examples, namely quantum phase estimation and quantum gate design, for which we achieve superior fidelity and scalability than obtained using greedy algorithms.

Single-shot Adaptive Measurement for Quantum-enhanced Metrology

Quantum-enhanced metrology aims to estimate an unknown parameter such that the precision scales better than the shot-noise bound. Single-shot adaptive quantum-enhanced metrology (AQEM) is a promising approach that uses feedback to tweak the quantum process according to previous measurement outcomes. Techniques and formalism for the adaptive case are quite different from the usual non-adaptive quantum metrology approach due to the causal relationship between measurements and outcomes. We construct a formal framework for AQEM by modeling the procedure as a decision-making process, and we derive the imprecision and the Cram\'{e}r-Rao lower bound with explicit dependence on the feedback policy. We also explain the reinforcement learning approach for generating quantum control policies, which is adopted due to the optimal policy being non-trivial to devise. Applying a learning algorithm based on differential evolution enables us to attain imprecision for adaptive interferometric phase estimation, which turns out to be SQL when non-entangled particles are used in the scheme.