Expressive power of tensor-network factorizations for probabilistic modeling, with applications from hidden Markov models to quantum machine learning

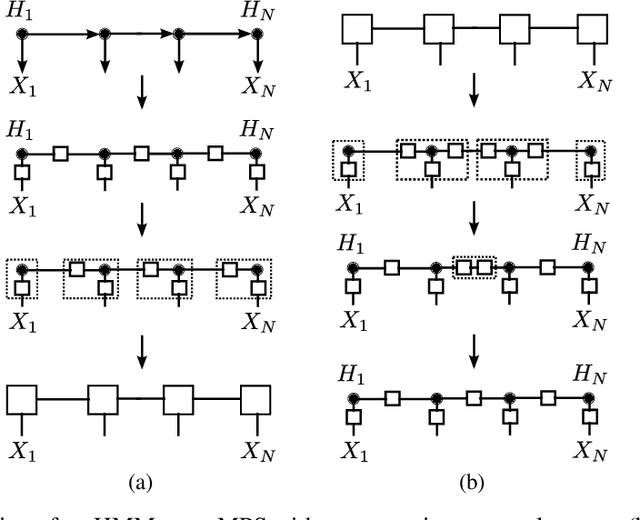
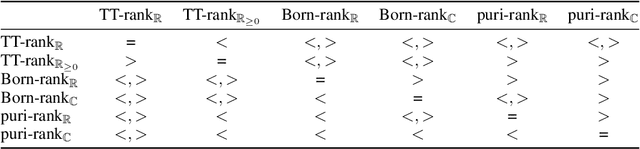
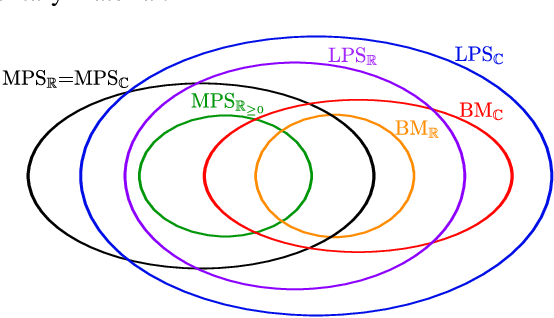
Tensor-network techniques have enjoyed outstanding success in physics, and have recently attracted attention in machine learning, both as a tool for the formulation of new learning algorithms and for enhancing the mathematical understanding of existing methods. Inspired by these developments, and the natural correspondence between tensor networks and probabilistic graphical models, we provide a rigorous analysis of the expressive power of various tensor-network factorizations of discrete multivariate probability distributions. These factorizations include non-negative tensor-trains/MPS, which are in correspondence with hidden Markov models, and Born machines, which are naturally related to local quantum circuits. When used to model probability distributions, they exhibit tractable likelihoods and admit efficient learning algorithms. Interestingly, we prove that there exist probability distributions for which there are unbounded separations between the resource requirements of some of these tensor-network factorizations. Particularly surprising is the fact that using complex instead of real tensors can lead to an arbitrarily large reduction in the number of parameters of the network. Additionally, we introduce locally purified states (LPS), a new factorization inspired by techniques for the simulation of quantum systems, with provably better expressive power than all other representations considered. The ramifications of this result are explored through numerical experiments. Our findings imply that LPS should be considered over hidden Markov models, and furthermore provide guidelines for the design of local quantum circuits for probabilistic modeling.

Supervised learning with generalized tensor networks

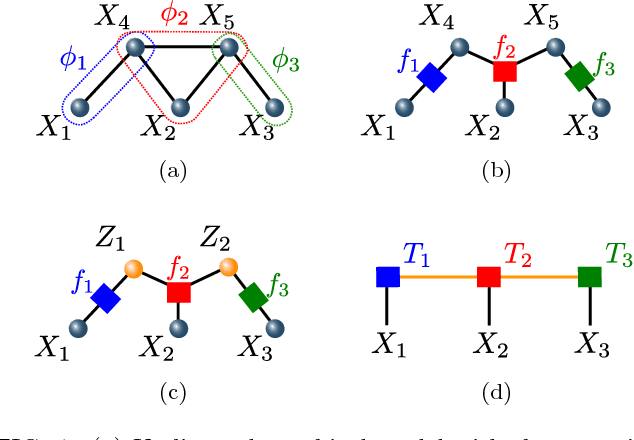
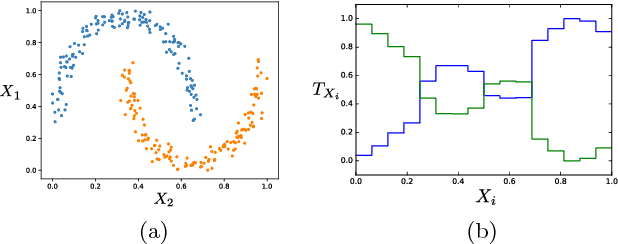
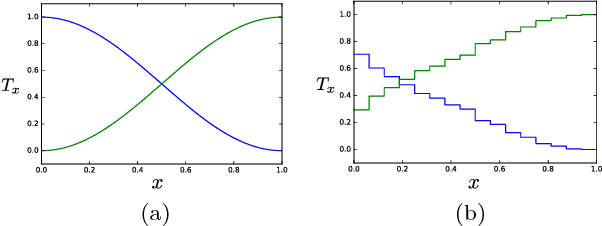
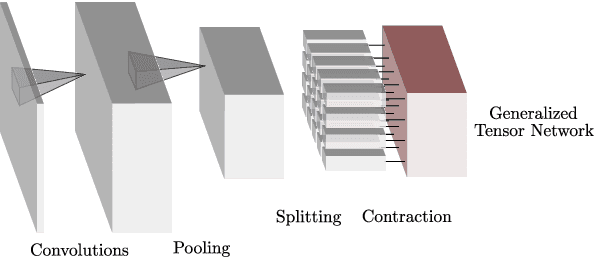
Tensor networks have found a wide use in a variety of applications in physics and computer science, recently leading to both theoretical insights as well as practical algorithms in machine learning. In this work we explore the connection between tensor networks and probabilistic graphical models, and show that it motivates the definition of generalized tensor networks where information from a tensor can be copied and reused in other parts of the network. We discuss the relationship between generalized tensor network architectures used in quantum physics, such as String-Bond States and Entangled Plaquette States, and architectures commonly used in machine learning. We provide an algorithm to train these networks in a supervised learning context and show that they overcome the limitations of regular tensor networks in higher dimensions, while keeping the computation efficient. A method to combine neural networks and tensor networks as part of a common deep learning architecture is also introduced. We benchmark our algorithm for several generalized tensor network architectures on the task of classifying images and sounds, and show that they outperform previously introduced tensor network algorithms. Some of the models we consider can be realized on a quantum computer and may guide the development of near-term quantum machine learning architectures.

Quantum Machine Learning

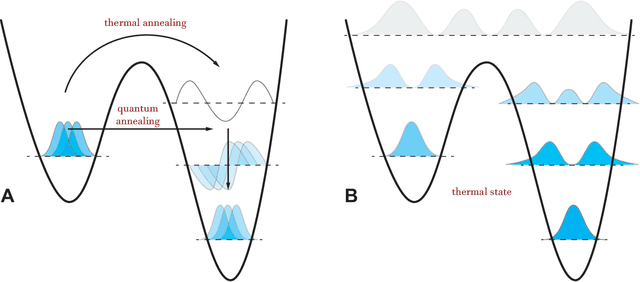
Fuelled by increasing computer power and algorithmic advances, machine learning techniques have become powerful tools for finding patterns in data. Since quantum systems produce counter-intuitive patterns believed not to be efficiently produced by classical systems, it is reasonable to postulate that quantum computers may outperform classical computers on machine learning tasks. The field of quantum machine learning explores how to devise and implement concrete quantum software that offers such advantages. Recent work has made clear that the hardware and software challenges are still considerable but has also opened paths towards solutions.

Neural-Network Quantum States, String-Bond States, and Chiral Topological States

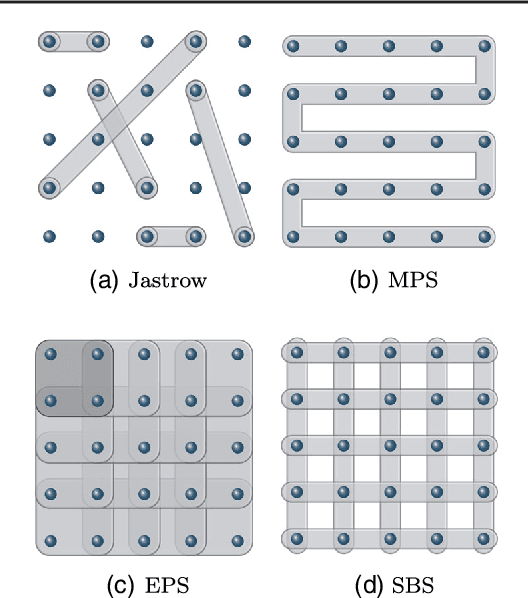
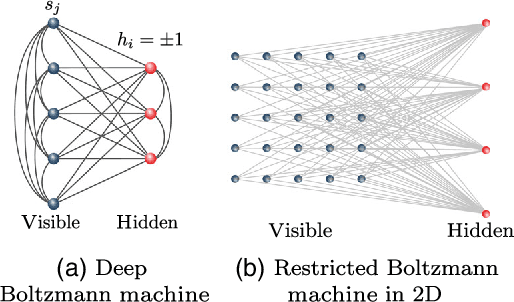
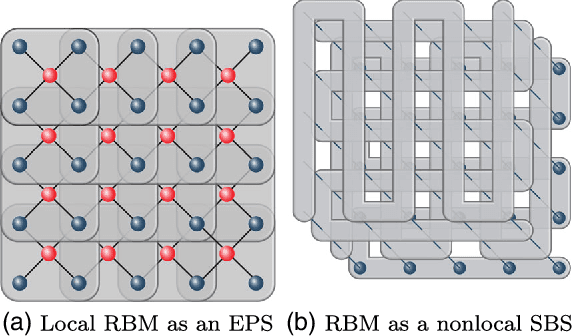
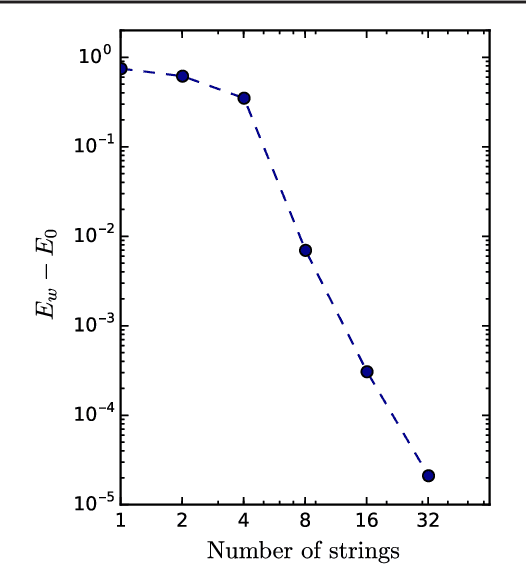
Neural-Network Quantum States have been recently introduced as an Ansatz for describing the wave function of quantum many-body systems. We show that there are strong connections between Neural-Network Quantum States in the form of Restricted Boltzmann Machines and some classes of Tensor-Network states in arbitrary dimensions. In particular we demonstrate that short-range Restricted Boltzmann Machines are Entangled Plaquette States, while fully connected Restricted Boltzmann Machines are String-Bond States with a nonlocal geometry and low bond dimension. These results shed light on the underlying architecture of Restricted Boltzmann Machines and their efficiency at representing many-body quantum states. String-Bond States also provide a generic way of enhancing the power of Neural-Network Quantum States and a natural generalization to systems with larger local Hilbert space. We compare the advantages and drawbacks of these different classes of states and present a method to combine them together. This allows us to benefit from both the entanglement structure of Tensor Networks and the efficiency of Neural-Network Quantum States into a single Ansatz capable of targeting the wave function of strongly correlated systems. While it remains a challenge to describe states with chiral topological order using traditional Tensor Networks, we show that Neural-Network Quantum States and their String-Bond States extension can describe a lattice Fractional Quantum Hall state exactly. In addition, we provide numerical evidence that Neural-Network Quantum States can approximate a chiral spin liquid with better accuracy than Entangled Plaquette States and local String-Bond States. Our results demonstrate the efficiency of neural networks to describe complex quantum wave functions and pave the way towards the use of String-Bond States as a tool in more traditional machine-learning applications.

Supervised quantum gate "teaching" for quantum hardware design

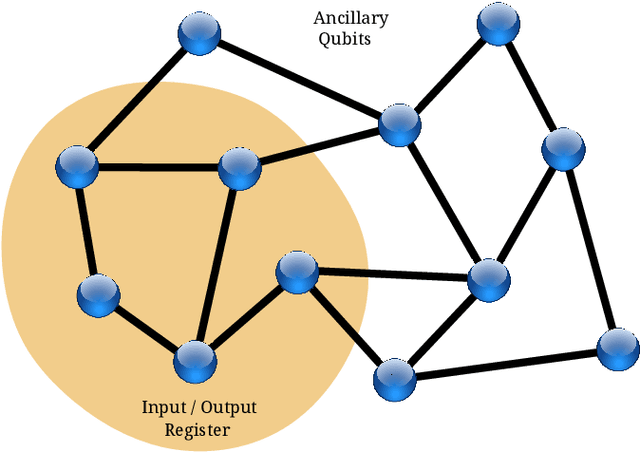
We show how to train a quantum network of pairwise interacting qubits such that its evolution implements a target quantum algorithm into a given network subset. Our strategy is inspired by supervised learning and is designed to help the physical construction of a quantum computer which operates with minimal external classical control.