Barry C. Sanders
Artificial intelligence for representing and characterizing quantum systems
Sep 05, 2025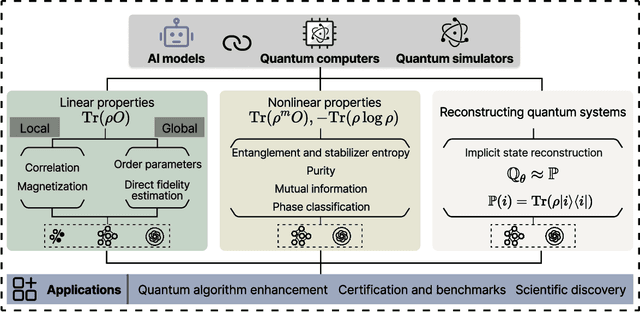

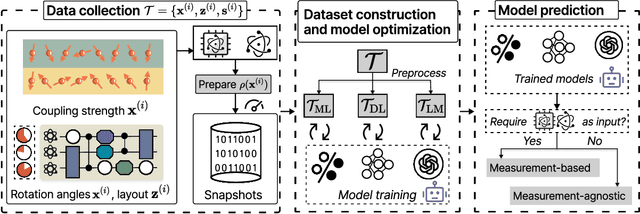
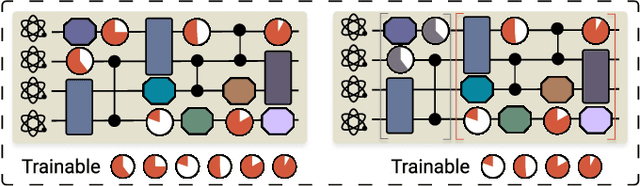
Abstract:Efficient characterization of large-scale quantum systems, especially those produced by quantum analog simulators and megaquop quantum computers, poses a central challenge in quantum science due to the exponential scaling of the Hilbert space with respect to system size. Recent advances in artificial intelligence (AI), with its aptitude for high-dimensional pattern recognition and function approximation, have emerged as a powerful tool to address this challenge. A growing body of research has leveraged AI to represent and characterize scalable quantum systems, spanning from theoretical foundations to experimental realizations. Depending on how prior knowledge and learning architectures are incorporated, the integration of AI into quantum system characterization can be categorized into three synergistic paradigms: machine learning, and, in particular, deep learning and language models. This review discusses how each of these AI paradigms contributes to two core tasks in quantum systems characterization: quantum property prediction and the construction of surrogates for quantum states. These tasks underlie diverse applications, from quantum certification and benchmarking to the enhancement of quantum algorithms and the understanding of strongly correlated phases of matter. Key challenges and open questions are also discussed, together with future prospects at the interface of AI and quantum science.
Quantum-Assisted Support Vector Regression for Detecting Facial Landmarks
Nov 17, 2021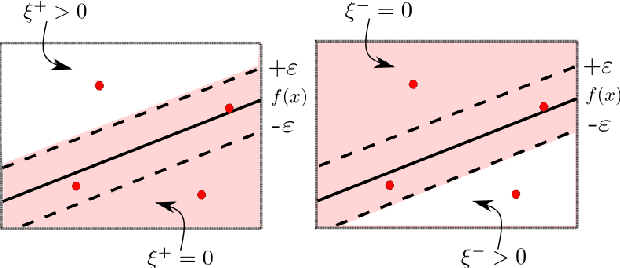

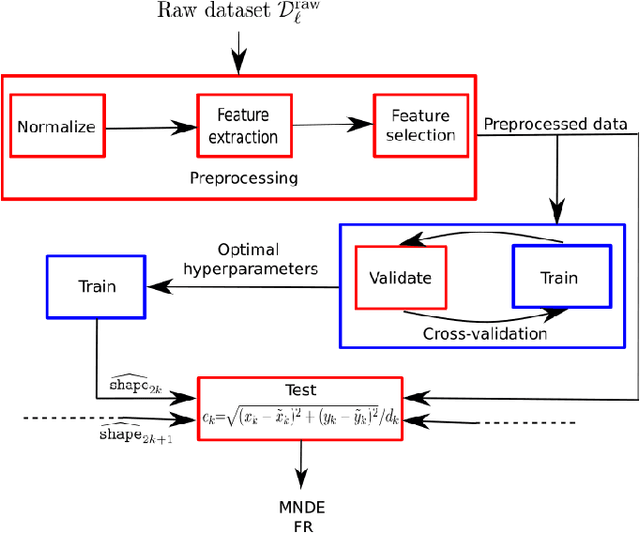
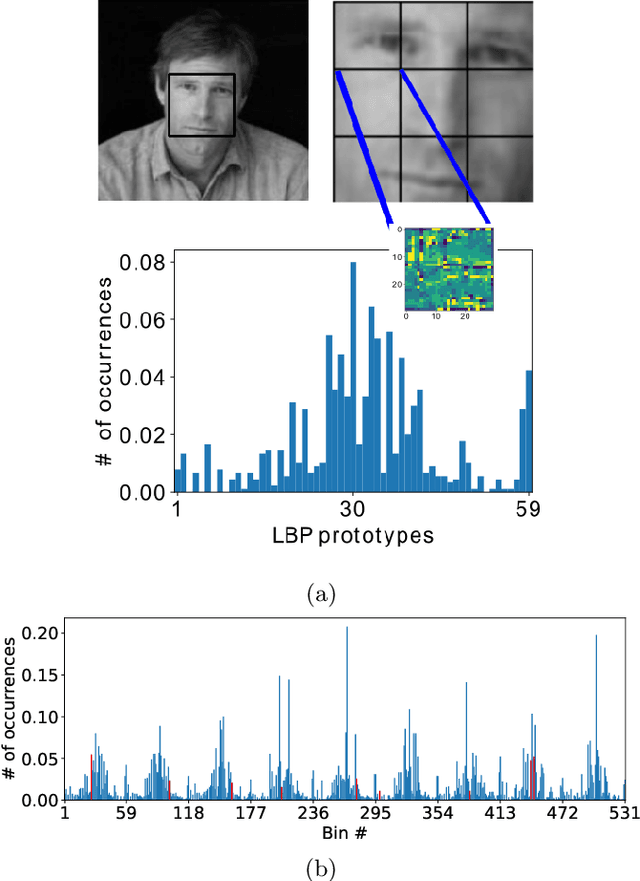
Abstract:The classical machine-learning model for support vector regression (SVR) is widely used for regression tasks, including weather prediction, stock-market and real-estate pricing. However, a practically realisable quantum version for SVR remains to be formulated. We devise annealing-based algorithms, namely simulated and quantum-classical hybrid, for training two SVR models, and compare their empirical performances against the SVR implementation of Python's scikit-learn package and the SVR-based state-of-the-art algorithm for the facial landmark detection (FLD) problem. Our method is to derive a quadratic-unconstrained-binary formulation for the optimisation problem used for training a SVR model and solve this problem using annealing. Using D-Wave's Hybrid Solver, we construct a quantum-assisted SVR model, thereby demonstrating a slight advantage over classical models regarding landmark-detection accuracy. Furthermore, we observe that annealing-based SVR models predict landmarks with lower variances compared to the SVR models trained by greedy optimisation procedures. Our work is a proof-of-concept example for applying quantu-assisted SVR to a supervised learning task with a small training dataset.
Quantum Multiple Kernel Learning
Nov 19, 2020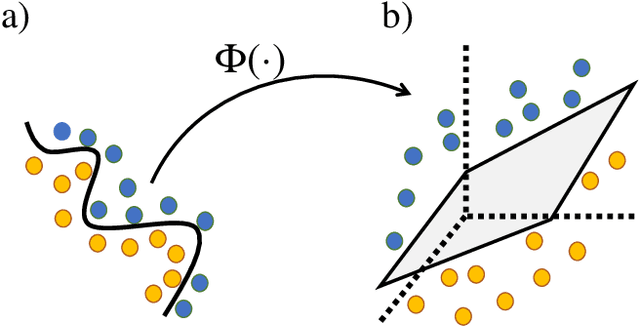

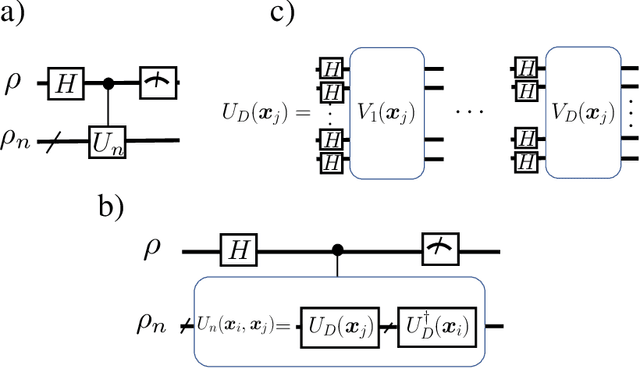
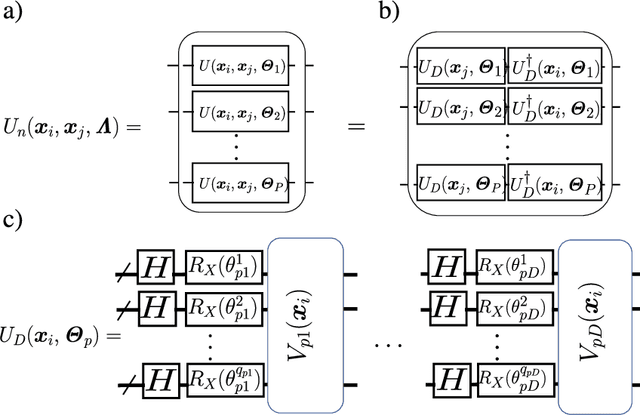
Abstract:Kernel methods play an important role in machine learning applications due to their conceptual simplicity and superior performance on numerous machine learning tasks. Expressivity of a machine learning model, referring to the ability of the model to approximate complex functions, has a significant influence on its performance in these tasks. One approach to enhancing the expressivity of kernel machines is to combine multiple individual kernels to arrive at a more expressive combined kernel. This approach is referred to as multiple kernel learning (MKL). In this work, we propose an MKL method we refer to as quantum MKL, which combines multiple quantum kernels. Our method leverages the power of deterministic quantum computing with one qubit (DQC1) to estimate the combined kernel for a set of classically intractable individual quantum kernels. The combined kernel estimation is achieved without explicitly computing each individual kernel, while still allowing for the tuning of individual kernels in order to achieve better expressivity. Our simulations on two binary classification problems---one performed on a synthetic dataset and the other on a German credit dataset---demonstrate the superiority of the quantum MKL method over single quantum kernel machines.
Robustness of Adaptive Quantum-Enhanced Phase Estimation
Sep 14, 2018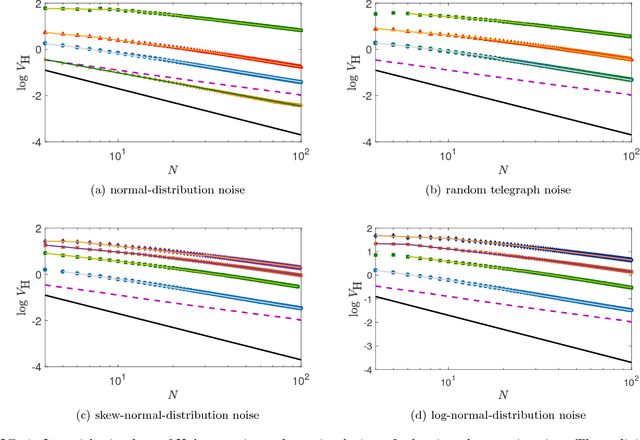
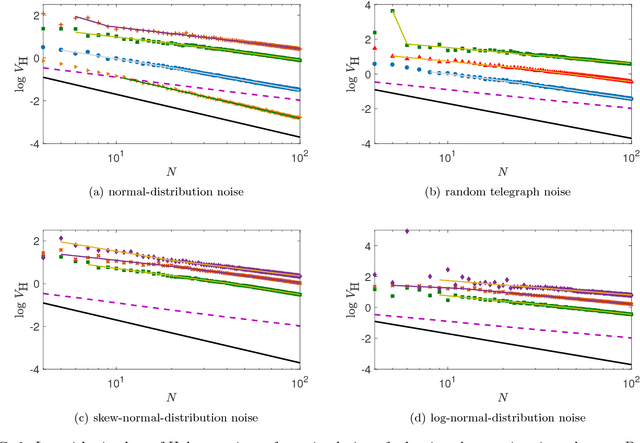
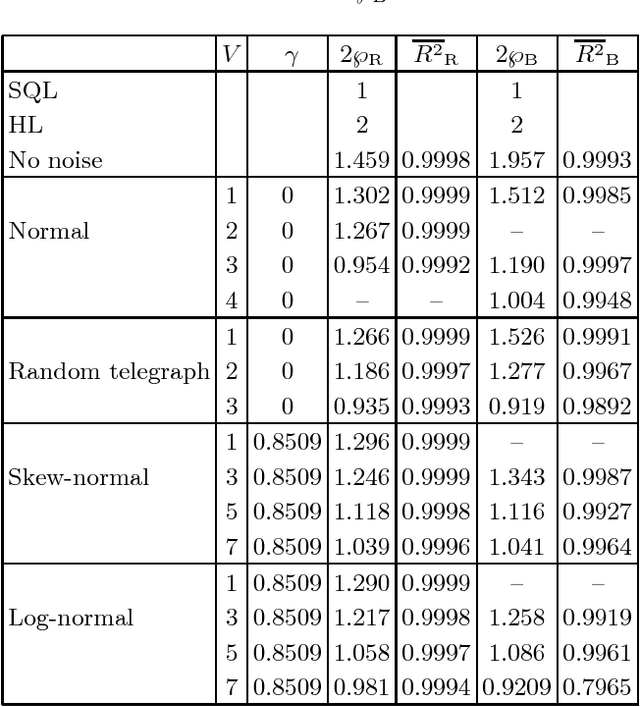
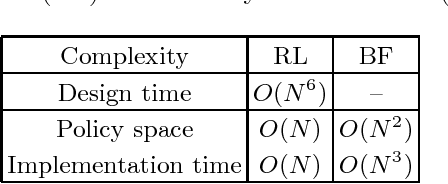
Abstract:As all physical adaptive quantum-enhanced metrology schemes operate under noisy conditions with only partially understood noise characteristics, so a practical control policy must be robust even for unknown noise. We aim to devise a test to evaluate the robustness of AQEM policies and assess the resource used by the policies. The robustness test is performed on adaptive phase estimation by simulating the scheme under four phase noise models corresponding to the normal-distribution noise, the random telegraph noise, the skew-normal-distribution noise, and the log-normal-distribution noise. The control policies are devised either by a reinforcement-learning algorithm in the same noise condition, albeit ignorant of its properties, or a Bayesian-based feedback method that assumes no noise. Our robustness test and resource comparison can be used to determining the efficacy and selecting a suitable policy.
Learning in Quantum Control: High-Dimensional Global Optimization for Noisy Quantum Dynamics
Nov 25, 2016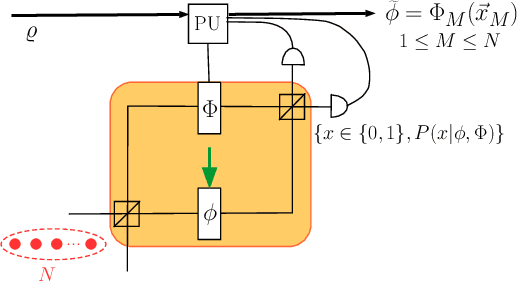

Abstract:Quantum control is valuable for various quantum technologies such as high-fidelity gates for universal quantum computing, adaptive quantum-enhanced metrology, and ultra-cold atom manipulation. Although supervised machine learning and reinforcement learning are widely used for optimizing control parameters in classical systems, quantum control for parameter optimization is mainly pursued via gradient-based greedy algorithms. Although the quantum fitness landscape is often compatible with greedy algorithms, sometimes greedy algorithms yield poor results, especially for large-dimensional quantum systems. We employ differential evolution algorithms to circumvent the stagnation problem of non-convex optimization. We improve quantum control fidelity for noisy system by averaging over the objective function. To reduce computational cost, we introduce heuristics for early termination of runs and for adaptive selection of search subspaces. Our implementation is massively parallel and vectorized to reduce run time even further. We demonstrate our methods with two examples, namely quantum phase estimation and quantum gate design, for which we achieve superior fidelity and scalability than obtained using greedy algorithms.
* 32 pages, 4 figures, extension of proceedings in ESANN 2016 conference submitted to Neurocomputing
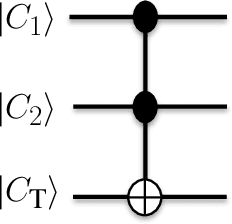
Designing High-Fidelity Single-Shot Three-Qubit Gates: A Machine Learning Approach
Oct 23, 2016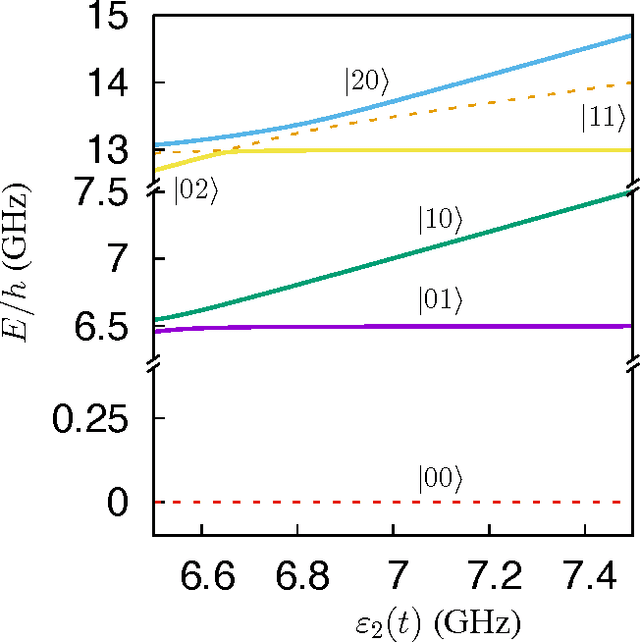
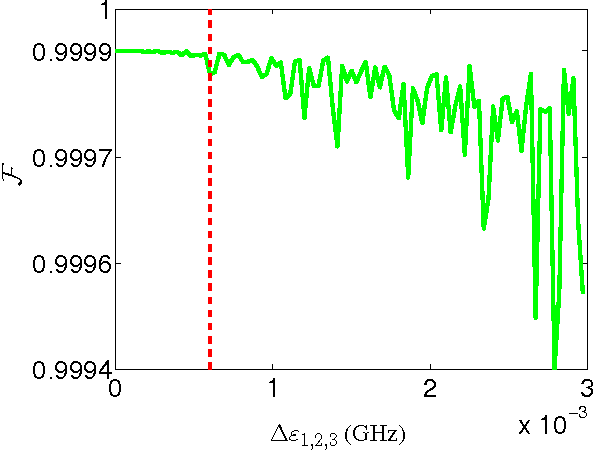
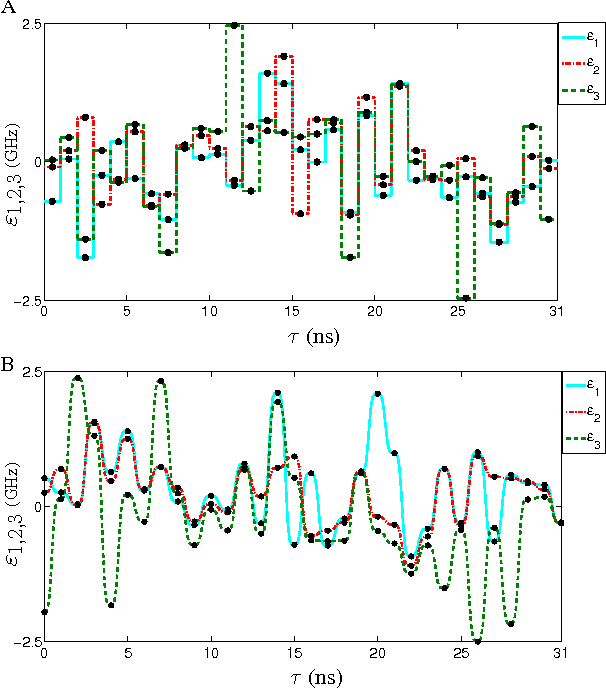
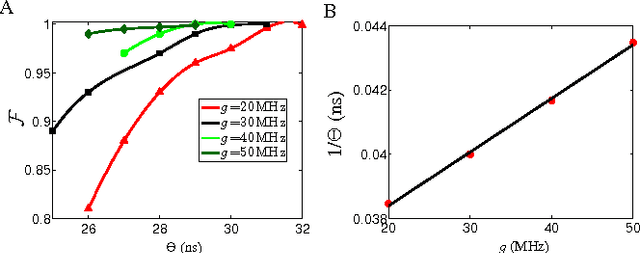
Abstract:Three-qubit quantum gates are key ingredients for quantum error correction and quantum information processing. We generate quantum-control procedures to design three types of three-qubit gates, namely Toffoli, Controlled-Not-Not and Fredkin gates. The design procedures are applicable to a system comprising three nearest-neighbor-coupled superconducting artificial atoms. For each three-qubit gate, the numerical simulation of the proposed scheme achieves 99.9% fidelity, which is an accepted threshold fidelity for fault-tolerant quantum computing. We test our procedure in the presence of decoherence-induced noise as well as show its robustness against random external noise generated by the control electronics. The three-qubit gates are designed via the machine learning algorithm called Subspace-Selective Self-Adaptive Differential Evolution (SuSSADE).
* 18 pages, 13 figures. Accepted for publication in Phys. Rev. Applied
Single-shot Adaptive Measurement for Quantum-enhanced Metrology
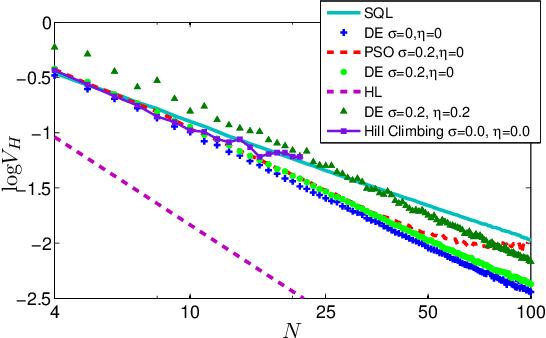
Aug 22, 2016Abstract:Quantum-enhanced metrology aims to estimate an unknown parameter such that the precision scales better than the shot-noise bound. Single-shot adaptive quantum-enhanced metrology (AQEM) is a promising approach that uses feedback to tweak the quantum process according to previous measurement outcomes. Techniques and formalism for the adaptive case are quite different from the usual non-adaptive quantum metrology approach due to the causal relationship between measurements and outcomes. We construct a formal framework for AQEM by modeling the procedure as a decision-making process, and we derive the imprecision and the Cram\'{e}r-Rao lower bound with explicit dependence on the feedback policy. We also explain the reinforcement learning approach for generating quantum control policies, which is adopted due to the optimal policy being non-trivial to devise. Applying a learning algorithm based on differential evolution enables us to attain imprecision for adaptive interferometric phase estimation, which turns out to be SQL when non-entangled particles are used in the scheme.
* 11 pages, 4 figures, paper accepted for Quantum Communications and Quantum Imaging XIV conference at SPIE Optics + Photonics 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge