A Review of Barren Plateaus in Variational Quantum Computing

Variational quantum computing offers a flexible computational paradigm with applications in diverse areas. However, a key obstacle to realizing their potential is the Barren Plateau (BP) phenomenon. When a model exhibits a BP, its parameter optimization landscape becomes exponentially flat and featureless as the problem size increases. Importantly, all the moving pieces of an algorithm -- choices of ansatz, initial state, observable, loss function and hardware noise -- can lead to BPs when ill-suited. Due to the significant impact of BPs on trainability, researchers have dedicated considerable effort to develop theoretical and heuristic methods to understand and mitigate their effects. As a result, the study of BPs has become a thriving area of research, influencing and cross-fertilizing other fields such as quantum optimal control, tensor networks, and learning theory. This article provides a comprehensive review of the current understanding of the BP phenomenon.

Tensor networks in machine learning

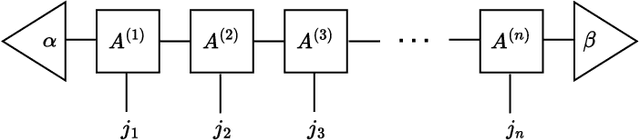
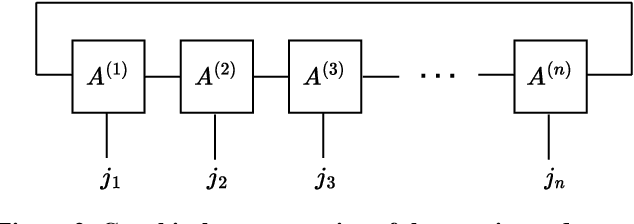
A tensor network is a type of decomposition used to express and approximate large arrays of data. A given data-set, quantum state or higher dimensional multi-linear map is factored and approximated by a composition of smaller multi-linear maps. This is reminiscent to how a Boolean function might be decomposed into a gate array: this represents a special case of tensor decomposition, in which the tensor entries are replaced by 0, 1 and the factorisation becomes exact. The collection of associated techniques are called, tensor network methods: the subject developed independently in several distinct fields of study, which have more recently become interrelated through the language of tensor networks. The tantamount questions in the field relate to expressability of tensor networks and the reduction of computational overheads. A merger of tensor networks with machine learning is natural. On the one hand, machine learning can aid in determining a factorization of a tensor network approximating a data set. On the other hand, a given tensor network structure can be viewed as a machine learning model. Herein the tensor network parameters are adjusted to learn or classify a data-set. In this survey we recover the basics of tensor networks and explain the ongoing effort to develop the theory of tensor networks in machine learning.

Quantum machine learning channel discrimination

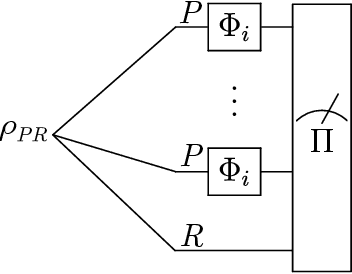
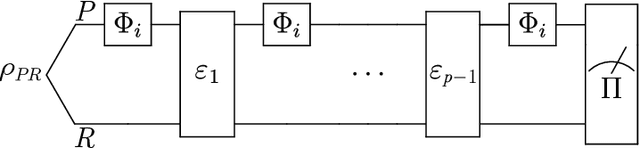
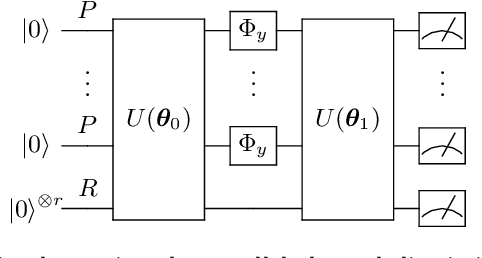
In the problem of quantum channel discrimination, one distinguishes between a given number of quantum channels, which is done by sending an input state through a channel and measuring the output state. This work studies applications of variational quantum circuits and machine learning techniques for discriminating such channels. In particular, we explore (i) the practical implementation of embedding this task into the framework of variational quantum computing, (ii) training a quantum classifier based on variational quantum circuits, and (iii) applying the quantum kernel estimation technique. For testing these three channel discrimination approaches, we considered a pair of entanglement-breaking channels and the depolarizing channel with two different depolarization factors. For the approach (i), we address solving the quantum channel discrimination problem using widely discussed parallel and sequential strategies. We show the advantage of the latter in terms of better convergence with less quantum resources. Quantum channel discrimination with a variational quantum classifier (ii) allows one to operate even with random and mixed input states and simple variational circuits. The kernel-based classification approach (iii) is also found effective as it allows one to discriminate depolarizing channels associated not with just fixed values of the depolarization factor, but with ranges of it. Additionally, we discovered that a simple modification of one of the commonly used kernels significantly increases the efficiency of this approach. Finally, our numerical findings reveal that the performance of variational methods of channel discrimination depends on the trace of the product of the output states. These findings demonstrate that quantum machine learning can be used to discriminate channels, such as those representing physical noise processes.

Experimental quantum adversarial learning with programmable superconducting qubits

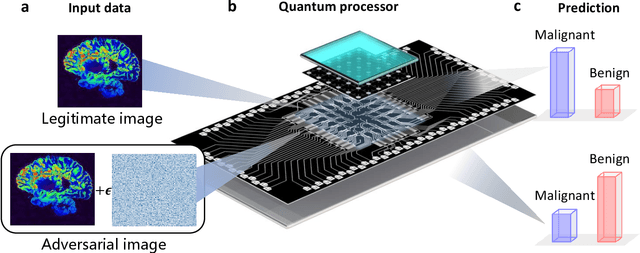
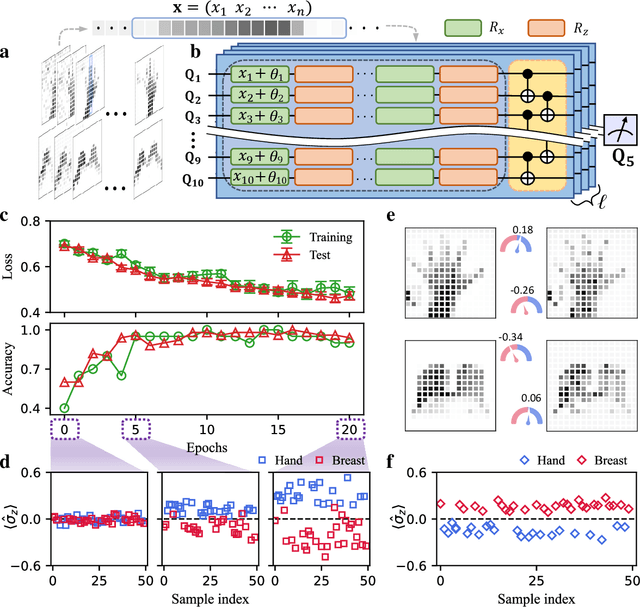
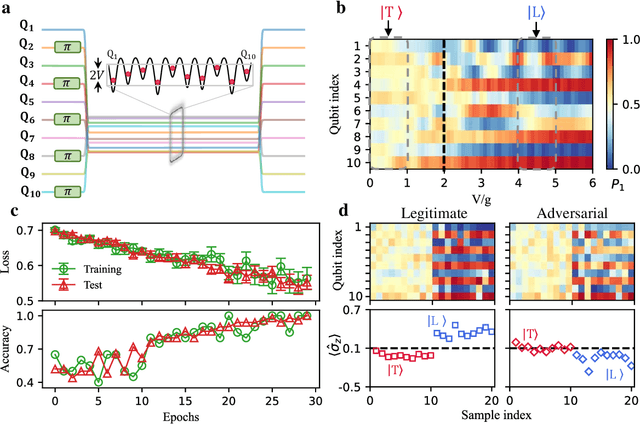
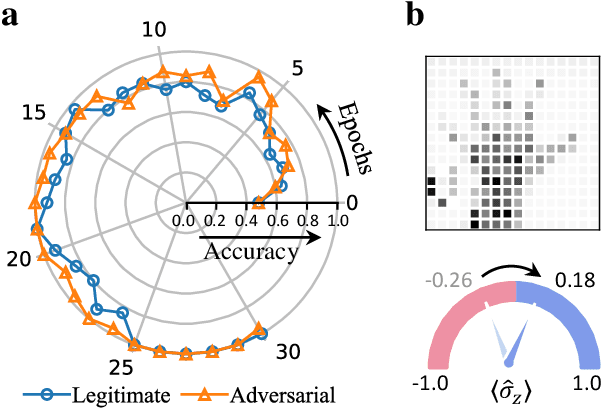
Quantum computing promises to enhance machine learning and artificial intelligence. Different quantum algorithms have been proposed to improve a wide spectrum of machine learning tasks. Yet, recent theoretical works show that, similar to traditional classifiers based on deep classical neural networks, quantum classifiers would suffer from the vulnerability problem: adding tiny carefully-crafted perturbations to the legitimate original data samples would facilitate incorrect predictions at a notably high confidence level. This will pose serious problems for future quantum machine learning applications in safety and security-critical scenarios. Here, we report the first experimental demonstration of quantum adversarial learning with programmable superconducting qubits. We train quantum classifiers, which are built upon variational quantum circuits consisting of ten transmon qubits featuring average lifetimes of 150 $\mu$s, and average fidelities of simultaneous single- and two-qubit gates above 99.94% and 99.4% respectively, with both real-life images (e.g., medical magnetic resonance imaging scans) and quantum data. We demonstrate that these well-trained classifiers (with testing accuracy up to 99%) can be practically deceived by small adversarial perturbations, whereas an adversarial training process would significantly enhance their robustness to such perturbations. Our results reveal experimentally a crucial vulnerability aspect of quantum learning systems under adversarial scenarios and demonstrate an effective defense strategy against adversarial attacks, which provide a valuable guide for quantum artificial intelligence applications with both near-term and future quantum devices.

On barren plateaus and cost function locality in variational quantum algorithms

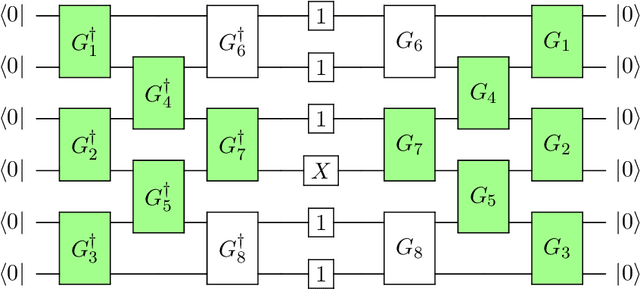
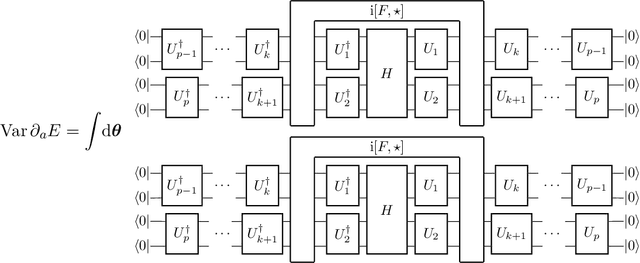
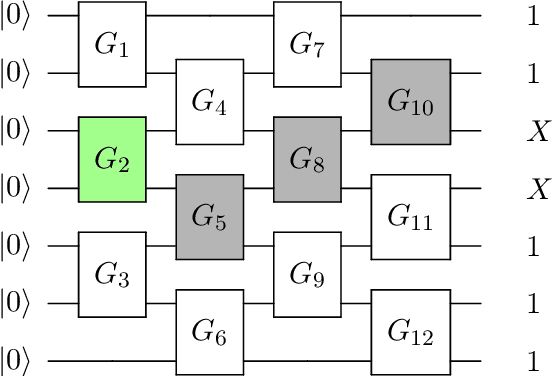
Variational quantum algorithms rely on gradient based optimization to iteratively minimize a cost function evaluated by measuring output(s) of a quantum processor. A barren plateau is the phenomenon of exponentially vanishing gradients in sufficiently expressive parametrized quantum circuits. It has been established that the onset of a barren plateau regime depends on the cost function, although the particular behavior has been demonstrated only for certain classes of cost functions. Here we derive a lower bound on the variance of the gradient, which depends mainly on the width of the circuit causal cone of each term in the Pauli decomposition of the cost function. Our result further clarifies the conditions under which barren plateaus can occur.

Self-learning eigenstates with a quantum processor

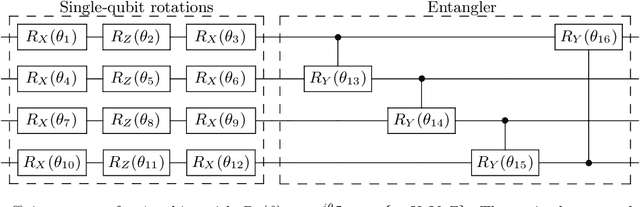
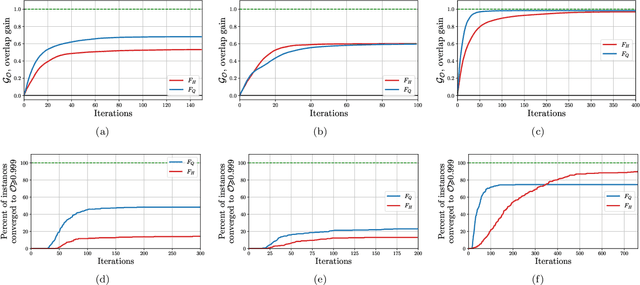
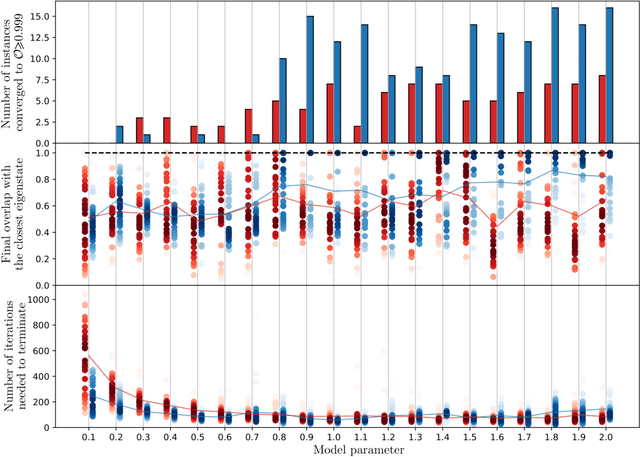
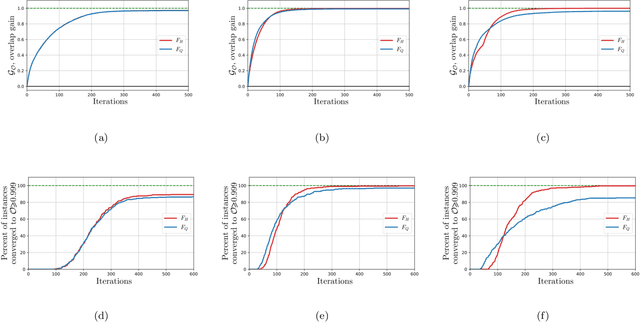
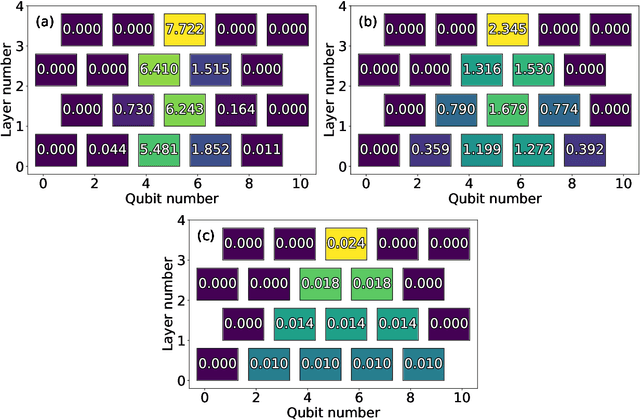
Solutions to many-body problem instances often involve an intractable number of degrees of freedom and admit no known approximations in general form. In practice, representing quantum-mechanical states of a given Hamiltonian using available numerical methods, in particular those based on variational Monte Carlo simulations, become exponentially more challenging with increasing system size. Recently quantum algorithms implemented as variational models, have been proposed to accelerate such simulations. The variational ansatz states are characterized by a polynomial number of parameters devised in a way to minimize the expectation value of a given Hamiltonian, which is emulated by local measurements. In this study, we develop a means to certify the termination of variational algorithms. We demonstrate our approach by applying it to three models: the transverse field Ising model, the model of one-dimensional spinless fermions with competing interactions and the Schwinger model of quantum electrodynamics. By means of comparison, we observe that our approach shows better performance near critical points in these models. We hence take a further step to improve the applicability and to certify the results of variational quantum simulators.

Variational Quantum Eigensolver for Frustrated Quantum Systems

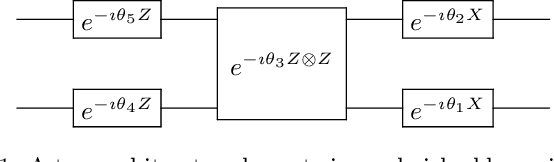
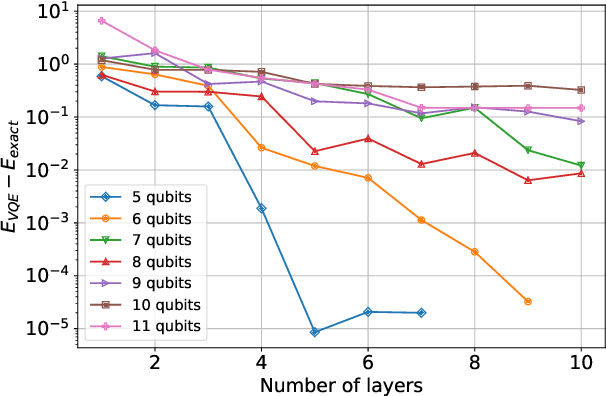
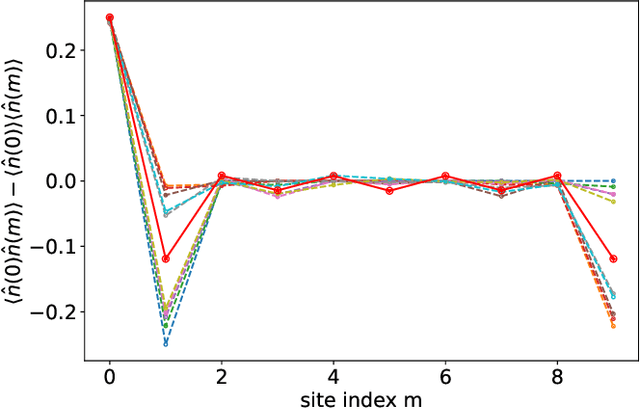
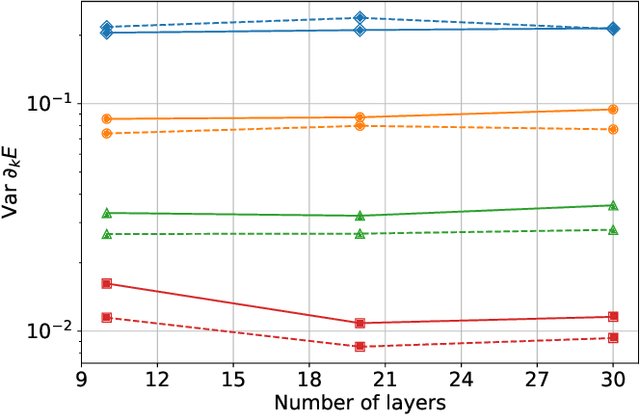
Hybrid quantum-classical algorithms have been proposed as a potentially viable application of quantum computers. A particular example -- the variational quantum eigensolver, or VQE -- is designed to determine a global minimum in an energy landscape specified by a quantum Hamiltonian, which makes it appealing for the needs of quantum chemistry. Experimental realizations have been reported in recent years and theoretical estimates of its efficiency are a subject of intense effort. Here we consider the performance of the VQE technique for a Hubbard-like model describing a one-dimensional chain of fermions with competing nearest- and next-nearest-neighbor interactions. We find that VQE is able to recover the correlation function of the ground state and the excitation velocities even when the energy convergence is not exact. We also study the barren plateau phenomenon for the Hamiltonians in question and find that the severity of this effect depends on the encoding of fermions to qubits. Our results are consistent with the current knowledge about the barren plateaus in quantum optimization.

Machine Learning Phase Transitions with a Quantum Processor

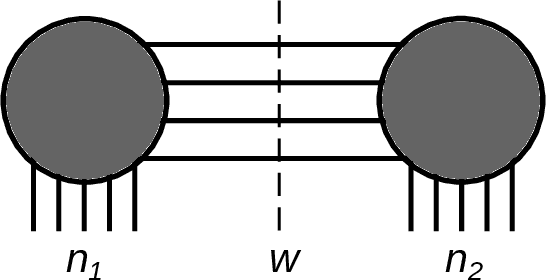
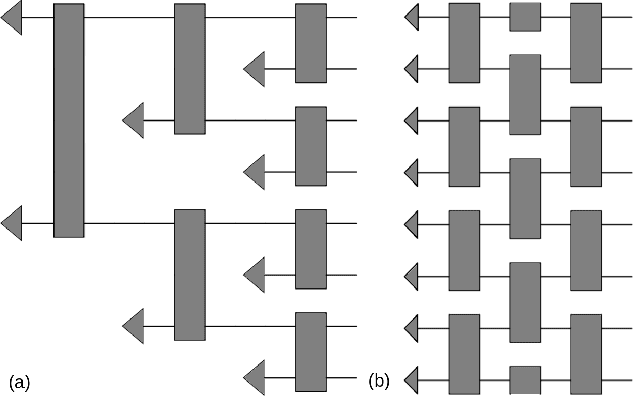
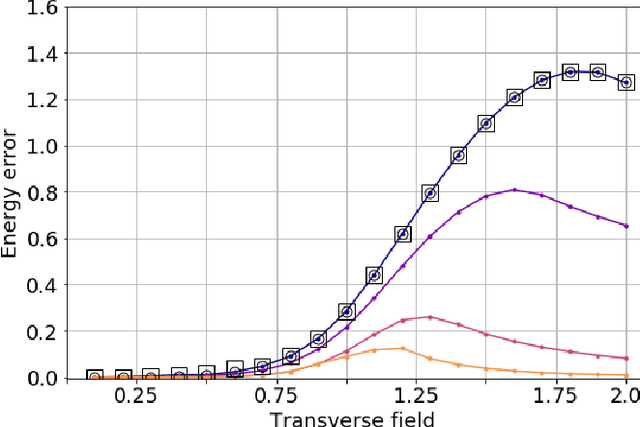
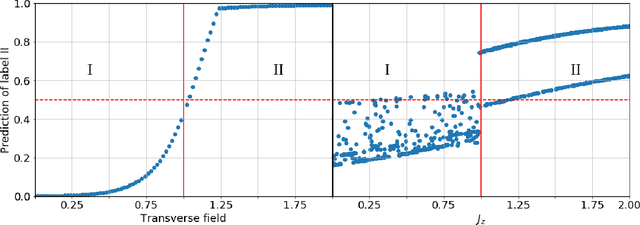
Machine learning has emerged as a promising approach to study the properties of many-body systems. Recently proposed as a tool to classify phases of matter, the approach relies on classical simulation methods$-$such as Monte Carlo$-$which are known to experience an exponential slowdown when simulating certain quantum systems. To overcome this slowdown while still leveraging machine learning, we propose a variational quantum algorithm which merges quantum simulation and quantum machine learning to classify phases of matter. Our classifier is directly fed labeled states recovered by the variational quantum eigensolver algorithm, thereby avoiding the data reading slowdown experienced in many applications of quantum enhanced machine learning. We propose families of variational ansatz states that are inspired directly by tensor networks. This allows us to use tools from tensor network theory to explain properties of the phase diagrams the presented method recovers. Finally, we propose a nearest-neighbour (checkerboard) quantum neural network. This majority vote quantum classifier is successfully trained to recognize phases of matter with $99\%$ accuracy for the transverse field Ising model and $94\%$ accuracy for the XXZ model. These findings suggest that our merger between quantum simulation and quantum enhanced machine learning offers a fertile ground to develop computational insights into quantum systems.

Experimental neural network enhanced quantum tomography

Quantum tomography is currently ubiquitous for testing any implementation of a quantum information processing device. Various sophisticated procedures for state and process reconstruction from measured data are well developed and benefit from precise knowledge of the model describing state preparation and the measurement apparatus. However, physical models suffer from intrinsic limitations as actual measurement operators and trial states cannot be known precisely. This scenario inevitably leads to state-preparation-and-measurement (SPAM) errors degrading reconstruction performance. Here we develop and experimentally implement a machine learning based protocol reducing SPAM errors. We trained a supervised neural network to filter the experimental data and hence uncovered salient patterns that characterize the measurement probabilities for the original state and the ideal experimental apparatus free from SPAM errors. We compared the neural network state reconstruction protocol with a protocol treating SPAM errors by process tomography, as well as to a SPAM-agnostic protocol with idealized measurements. The average reconstruction fidelity is shown to be enhanced by 10\% and 27\%, respectively. The presented methods apply to the vast range of quantum experiments which rely on tomography.

Quantum Machine Learning

Fuelled by increasing computer power and algorithmic advances, machine learning techniques have become powerful tools for finding patterns in data. Since quantum systems produce counter-intuitive patterns believed not to be efficiently produced by classical systems, it is reasonable to postulate that quantum computers may outperform classical computers on machine learning tasks. The field of quantum machine learning explores how to devise and implement concrete quantum software that offers such advantages. Recent work has made clear that the hardware and software challenges are still considerable but has also opened paths towards solutions.