Symmetric observations without symmetric causal explanations

Inferring causal models from observed correlations is a challenging task, crucial to many areas of science. In order to alleviate the effort, it is important to know whether symmetries in the observations correspond to symmetries in the underlying realization. Via an explicit example, we answer this question in the negative. We use a tripartite probability distribution over binary events that is realized by using three (different) independent sources of classical randomness. We prove that even removing the condition that the sources distribute systems described by classical physics, the requirements that i) the sources distribute the same physical systems, ii) these physical systems respect relativistic causality, and iii) the correlations are the observed ones, are incompatible.

Tensorization of neural networks for improved privacy and interpretability

We present a tensorization algorithm for constructing tensor train representations of functions, drawing on sketching and cross interpolation ideas. The method only requires black-box access to the target function and a small set of sample points defining the domain of interest. Thus, it is particularly well-suited for machine learning models, where the domain of interest is naturally defined by the training dataset. We show that this approach can be used to enhance the privacy and interpretability of neural network models. Specifically, we apply our decomposition to (i) obfuscate neural networks whose parameters encode patterns tied to the training data distribution, and (ii) estimate topological phases of matter that are easily accessible from the tensor train representation. Additionally, we show that this tensorization can serve as an efficient initialization method for optimizing tensor trains in general settings, and that, for model compression, our algorithm achieves a superior trade-off between memory and time complexity compared to conventional tensorization methods of neural networks.

Universal representation by Boltzmann machines with Regularised Axons

It is widely known that Boltzmann machines are capable of representing arbitrary probability distributions over the values of their visible neurons, given enough hidden ones. However, sampling -- and thus training -- these models can be numerically hard. Recently we proposed a regularisation of the connections of Boltzmann machines, in order to control the energy landscape of the model, paving a way for efficient sampling and training. Here we formally prove that such regularised Boltzmann machines preserve the ability to represent arbitrary distributions. This is in conjunction with controlling the number of energy local minima, thus enabling easy \emph{guided} sampling and training. Furthermore, we explicitly show that regularised Boltzmann machines can store exponentially many arbitrarily correlated visible patterns with perfect retrieval, and we connect them to the Dense Associative Memory networks.

TensorKrowch: Smooth integration of tensor networks in machine learning

Tensor networks are factorizations of high-dimensional tensors into networks of smaller tensors. They have applications in physics and mathematics, and recently have been proposed as promising machine learning architectures. To ease the integration of tensor networks in machine learning pipelines, we introduce TensorKrowch, an open source Python library built on top of PyTorch. Providing a user-friendly interface, TensorKrowch allows users to construct any tensor network, train it, and integrate it as a layer in more intricate deep learning models. In this paper, we describe the main functionality and basic usage of TensorKrowch, and provide technical details on its building blocks and the optimizations performed to achieve efficient operation.

Accelerating the training of single-layer binary neural networks using the HHL quantum algorithm

Binary Neural Networks are a promising technique for implementing efficient deep models with reduced storage and computational requirements. The training of these is however, still a compute-intensive problem that grows drastically with the layer size and data input. At the core of this calculation is the linear regression problem. The Harrow-Hassidim-Lloyd (HHL) quantum algorithm has gained relevance thanks to its promise of providing a quantum state containing the solution of a linear system of equations. The solution is encoded in superposition at the output of a quantum circuit. Although this seems to provide the answer to the linear regression problem for the training neural networks, it also comes with multiple, difficult-to-avoid hurdles. This paper shows, however, that useful information can be extracted from the quantum-mechanical implementation of HHL, and used to reduce the complexity of finding the solution on the classical side.

Physics solutions for machine learning privacy leaks

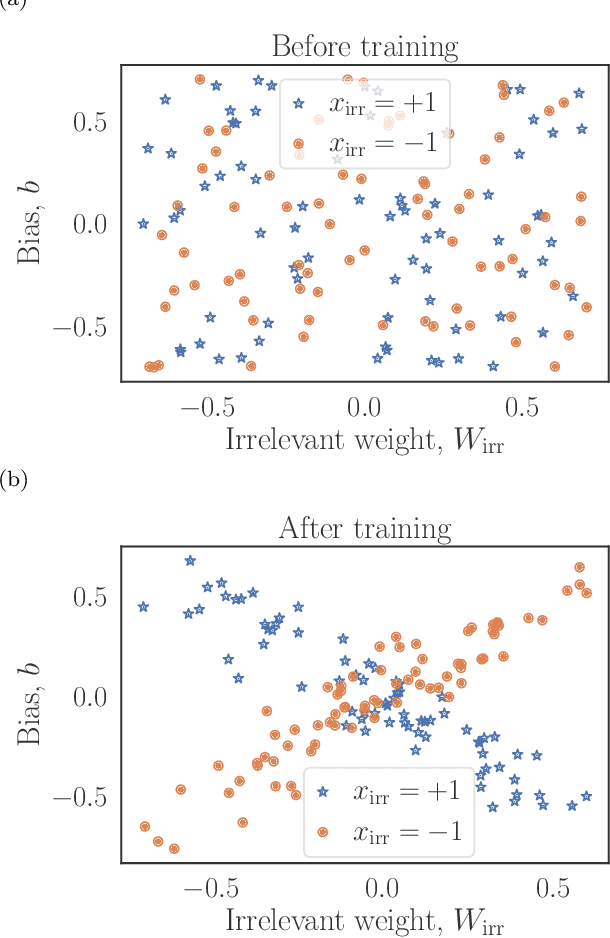
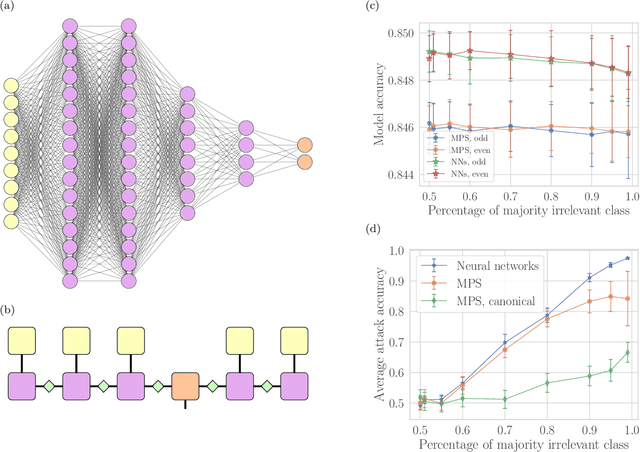
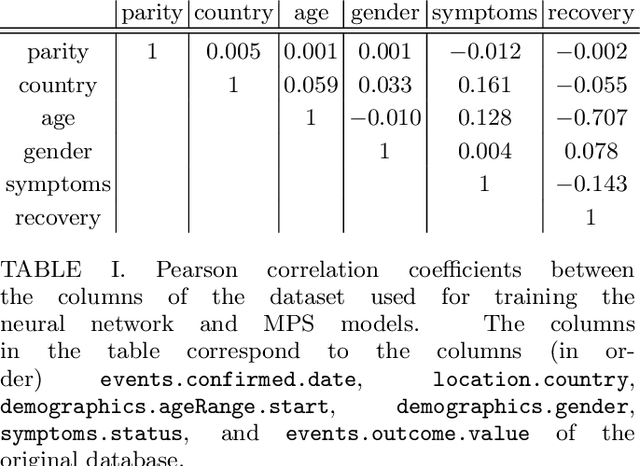
Machine learning systems are becoming more and more ubiquitous in increasingly complex areas, including cutting-edge scientific research. The opposite is also true: the interest in better understanding the inner workings of machine learning systems motivates their analysis under the lens of different scientific disciplines. Physics is particularly successful in this, due to its ability to describe complex dynamical systems. While explanations of phenomena in machine learning based on physics are increasingly present, examples of direct application of notions akin to physics in order to improve machine learning systems are more scarce. Here we provide one such application in the problem of developing algorithms that preserve the privacy of the manipulated data, which is especially important in tasks such as the processing of medical records. We develop well-defined conditions to guarantee robustness to specific types of privacy leaks, and rigorously prove that such conditions are satisfied by tensor-network architectures. These are inspired by the efficient representation of quantum many-body systems, and have shown to compete and even surpass traditional machine learning architectures in certain cases. Given the growing expertise in training tensor-network architectures, these results imply that one may not have to be forced to make a choice between accuracy in prediction and ensuring the privacy of the information processed.

Defence against adversarial attacks using classical and quantum-enhanced Boltzmann machines

We provide a robust defence to adversarial attacks on discriminative algorithms. Neural networks are naturally vulnerable to small, tailored perturbations in the input data that lead to wrong predictions. On the contrary, generative models attempt to learn the distribution underlying a dataset, making them inherently more robust to small perturbations. We use Boltzmann machines for discrimination purposes as attack-resistant classifiers, and compare them against standard state-of-the-art adversarial defences. We find improvements ranging from 5% to 72% against attacks with Boltzmann machines on the MNIST dataset. We furthermore complement the training with quantum-enhanced sampling from the D-Wave 2000Q annealer, finding results comparable with classical techniques and with marginal improvements in some cases. These results underline the relevance of probabilistic methods in constructing neural networks and demonstrate the power of quantum computers, even with limited hardware capabilities. This work is dedicated to the memory of Peter Wittek.

Efficient training of energy-based models via spin-glass control

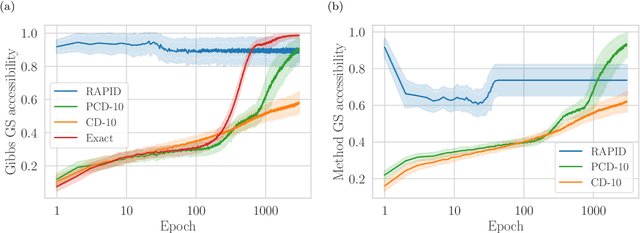
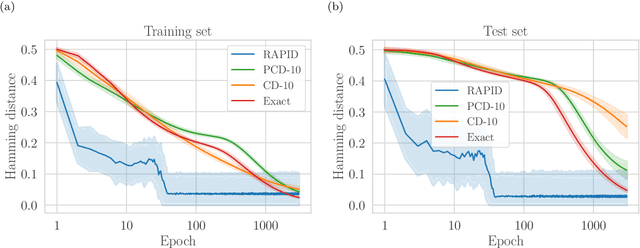
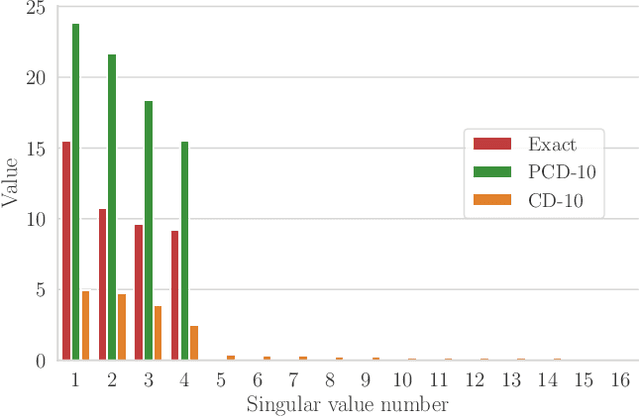
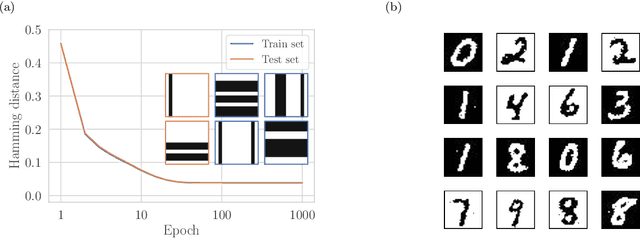
We present an efficient method for unsupervised learning using Boltzmann machines. The method is rooted in the control of the spin-glass properties of the Ising model described by the Boltzmann machine's weights. This allows for very easy access to low-energy configurations. We apply RAPID, the combination of Restricting the Axons (RA) of the model and training via Pattern-InDuced correlations (PID), to learn the Bars and Stripes dataset of various sizes and the MNIST dataset. We show how, in these tasks, RAPID quickly outperforms standard techniques for unsupervised learning in generalization ability. Indeed, both the number of epochs needed for effective learning and the computation time per training step are greatly reduced. In its simplest form, PID allows to compute the negative phase of the log-likelihood gradient with no Markov chain Monte Carlo sampling costs at all.

Quantum Inflation: A General Approach to Quantum Causal Compatibility

Causality is a seminal concept in science: any research discipline, from sociology and medicine to physics and chemistry, aims at understanding the causes that could explain the correlations observed among some measured variables. While several methods exist to characterize classical causal models, no general construction is known for the quantum case. In this work we present quantum inflation, a systematic technique to falsify if a given quantum causal model is compatible with some observed correlations. We demonstrate the power of the technique by reproducing known results and solving open problems for some paradigmatic examples of causal networks. Our results may find an application in many fields: from the characterization of correlations in quantum networks to the study of quantum effects in thermodynamic and biological processes.

Bayesian Deep Learning on a Quantum Computer

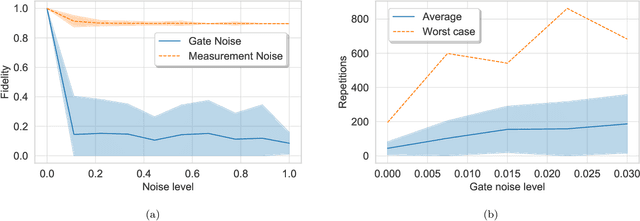
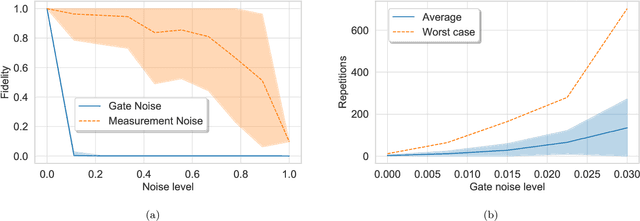
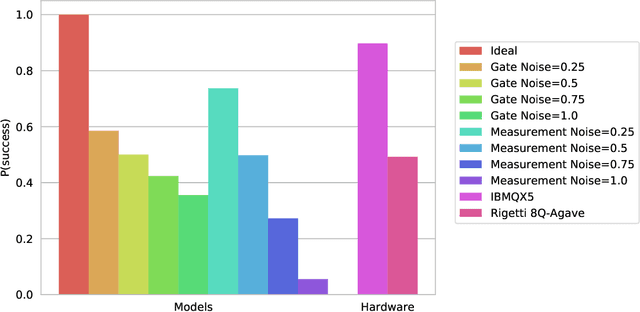
Bayesian methods in machine learning, such as Gaussian processes, have great advantages compared to other techniques. In particular, they provide estimates of the uncertainty associated with a prediction. Extending the Bayesian approach to deep architectures has remained a major challenge. Recent results connected deep feedforward neural networks with Gaussian processes, allowing training without backpropagation. This connection enables us to leverage a quantum algorithm designed for Gaussian processes and develop a new algorithm for Bayesian deep learning on quantum computers. The properties of the kernel matrix in the Gaussian process ensure the efficient execution of the core component of the protocol, quantum matrix inversion, providing an at least polynomial speedup over the classical algorithm. Furthermore, we demonstrate the execution of the algorithm on contemporary quantum computers and analyze its robustness with respect to realistic noise models.