Improving Landmark Localization with Semi-Supervised Learning

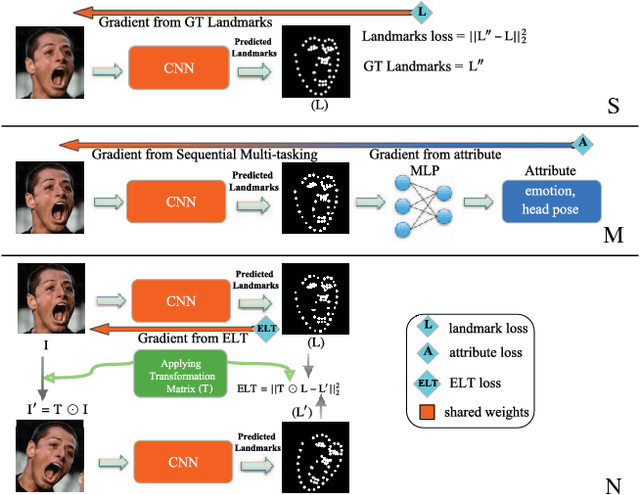
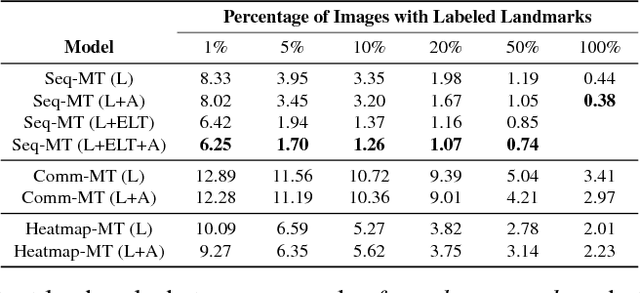
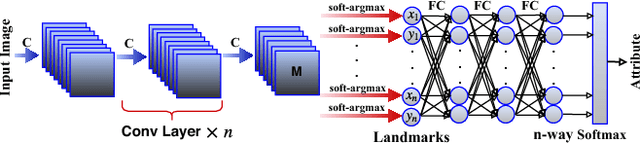
We present two techniques to improve landmark localization in images from partially annotated datasets. Our primary goal is to leverage the common situation where precise landmark locations are only provided for a small data subset, but where class labels for classification or regression tasks related to the landmarks are more abundantly available. First, we propose the framework of sequential multitasking and explore it here through an architecture for landmark localization where training with class labels acts as an auxiliary signal to guide the landmark localization on unlabeled data. A key aspect of our approach is that errors can be backpropagated through a complete landmark localization model. Second, we propose and explore an unsupervised learning technique for landmark localization based on having a model predict equivariant landmarks with respect to transformations applied to the image. We show that these techniques, improve landmark prediction considerably and can learn effective detectors even when only a small fraction of the dataset has landmark labels. We present results on two toy datasets and four real datasets, with hands and faces, and report new state-of-the-art on two datasets in the wild, e.g. with only 5\% of labeled images we outperform previous state-of-the-art trained on the AFLW dataset.

Randomized Value Functions via Multiplicative Normalizing Flows

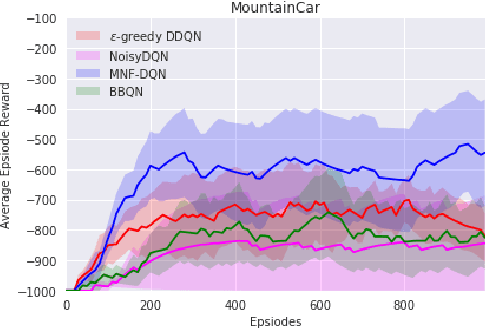
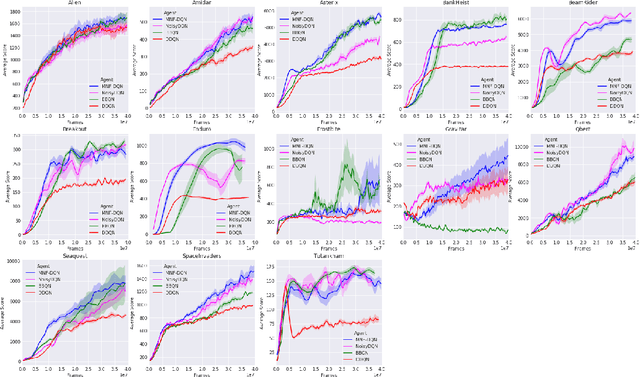
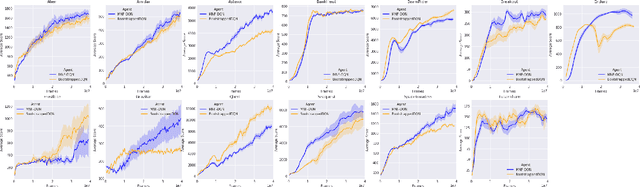
Randomized value functions offer a promising approach towards the challenge of efficient exploration in complex environments with high dimensional state and action spaces. Unlike traditional point estimate methods, randomized value functions maintain a posterior distribution over action-space values. This prevents the agent's behavior policy from prematurely exploiting early estimates and falling into local optima. In this work, we leverage recent advances in variational Bayesian neural networks and combine these with traditional Deep Q-Networks (DQN) and Deep Deterministic Policy Gradient (DDPG) to achieve randomized value functions for high-dimensional domains. In particular, we augment DQN and DDPG with multiplicative normalizing flows in order to track a rich approximate posterior distribution over the parameters of the value function. This allows the agent to perform approximate Thompson sampling in a computationally efficient manner via stochastic gradient methods. We demonstrate the benefits of our approach through an empirical comparison in high dimensional environments.

Convergent Tree Backup and Retrace with Function Approximation

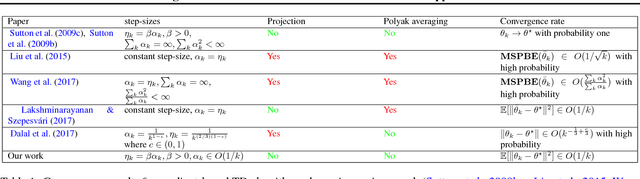
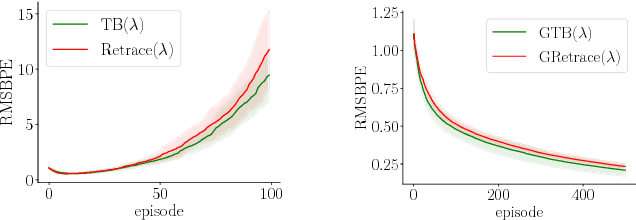
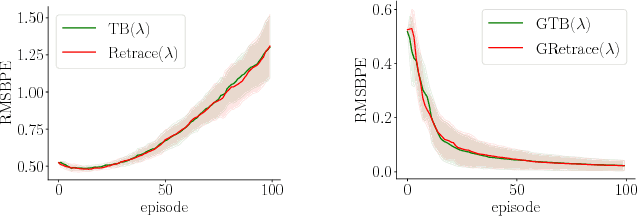
Off-policy learning is key to scaling up reinforcement learning as it allows to learn about a target policy from the experience generated by a different behavior policy. Unfortunately, it has been challenging to combine off-policy learning with function approximation and multi-step bootstrapping in a way that leads to both stable and efficient algorithms. In this work, we show that the \textsc{Tree Backup} and \textsc{Retrace} algorithms are unstable with linear function approximation, both in theory and in practice with specific examples. Based on our analysis, we then derive stable and efficient gradient-based algorithms using a quadratic convex-concave saddle-point formulation. By exploiting the problem structure proper to these algorithms, we are able to provide convergence guarantees and finite-sample bounds. The applicability of our new analysis also goes beyond \textsc{Tree Backup} and \textsc{Retrace} and allows us to provide new convergence rates for the GTD and GTD2 algorithms without having recourse to projections or Polyak averaging.

Parametric Adversarial Divergences are Good Task Losses for Generative Modeling

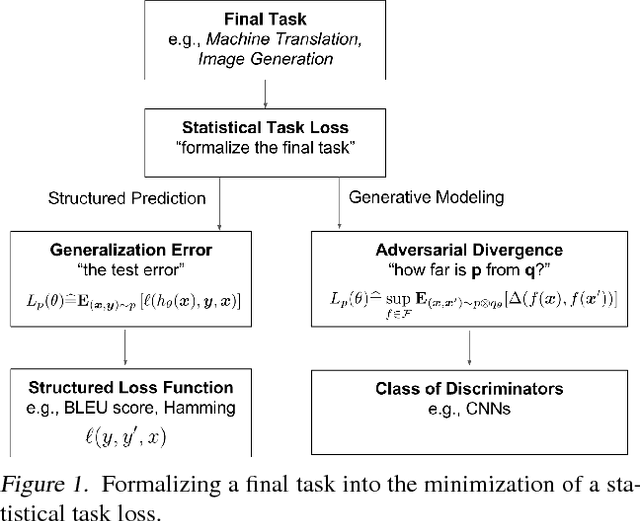
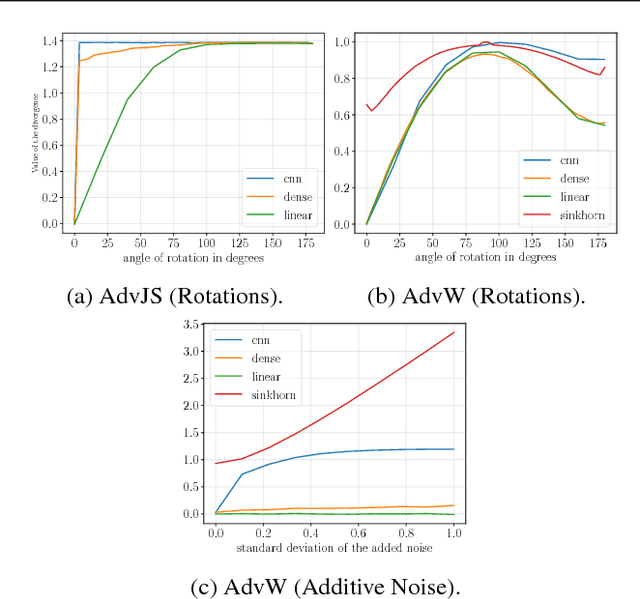
Generative modeling of high dimensional data like images is a notoriously difficult and ill-defined problem. In particular, how to evaluate a learned generative model is unclear. In this position paper, we argue that adversarial learning, pioneered with generative adversarial networks (GANs), provides an interesting framework to implicitly define more meaningful task losses for generative modeling tasks, such as for generating "visually realistic" images. We refer to those task losses as parametric adversarial divergences and we give two main reasons why we think parametric divergences are good learning objectives for generative modeling. Additionally, we unify the processes of choosing a good structured loss (in structured prediction) and choosing a discriminator architecture (in generative modeling) using statistical decision theory; we are then able to formalize and quantify the intuition that "weaker" losses are easier to learn from, in a specific setting. Finally, we propose two new challenging tasks to evaluate parametric and nonparametric divergences: a qualitative task of generating very high-resolution digits, and a quantitative task of learning data that satisfies high-level algebraic constraints. We use two common divergences to train a generator and show that the parametric divergence outperforms the nonparametric divergence on both the qualitative and the quantitative task.

Fast Approximate Natural Gradient Descent in a Kronecker-factored Eigenbasis

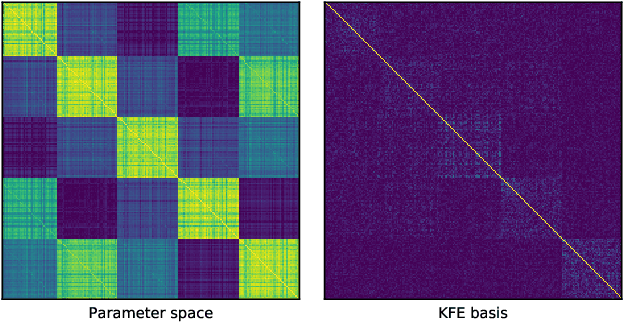
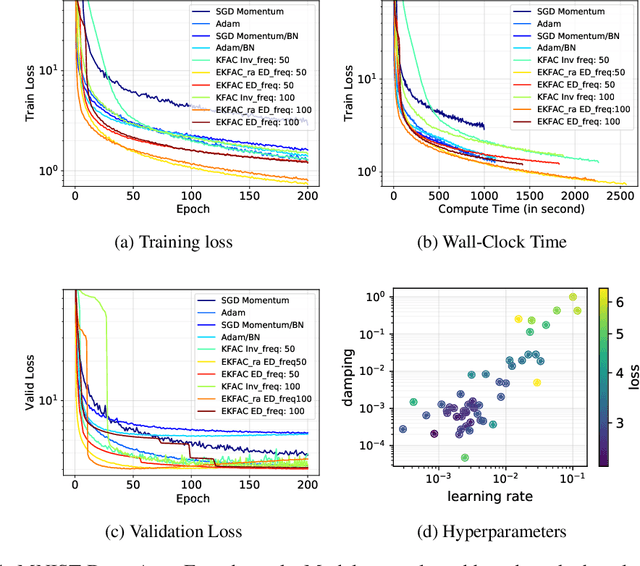
Optimization algorithms that leverage gradient covariance information, such as variants of natural gradient descent (Amari, 1998), offer the prospect of yielding more effective descent directions. For models with many parameters, the covariance matrix they are based on becomes gigantic, making them inapplicable in their original form. This has motivated research into both simple diagonal approximations and more sophisticated factored approximations such as KFAC (Heskes, 2000; Martens & Grosse, 2015; Grosse & Martens, 2016). In the present work we draw inspiration from both to propose a novel approximation that is provably better than KFAC and amendable to cheap partial updates. It consists in tracking a diagonal variance, not in parameter coordinates, but in a Kronecker-factored eigenbasis, in which the diagonal approximation is likely to be more effective. Experiments show improvements over KFAC in optimization speed for several deep network architectures.

Learning to Compute Word Embeddings On the Fly

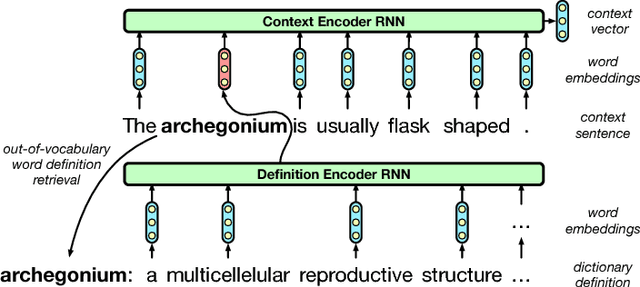
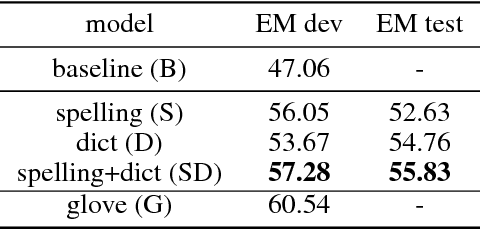
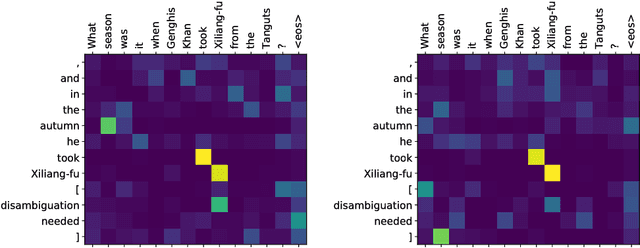
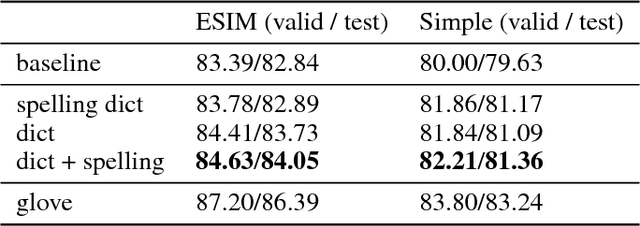
Words in natural language follow a Zipfian distribution whereby some words are frequent but most are rare. Learning representations for words in the "long tail" of this distribution requires enormous amounts of data. Representations of rare words trained directly on end tasks are usually poor, requiring us to pre-train embeddings on external data, or treat all rare words as out-of-vocabulary words with a unique representation. We provide a method for predicting embeddings of rare words on the fly from small amounts of auxiliary data with a network trained end-to-end for the downstream task. We show that this improves results against baselines where embeddings are trained on the end task for reading comprehension, recognizing textual entailment and language modeling.

Learning to Generate Samples from Noise through Infusion Training

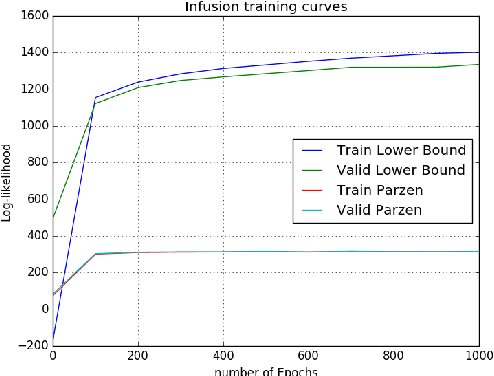
In this work, we investigate a novel training procedure to learn a generative model as the transition operator of a Markov chain, such that, when applied repeatedly on an unstructured random noise sample, it will denoise it into a sample that matches the target distribution from the training set. The novel training procedure to learn this progressive denoising operation involves sampling from a slightly different chain than the model chain used for generation in the absence of a denoising target. In the training chain we infuse information from the training target example that we would like the chains to reach with a high probability. The thus learned transition operator is able to produce quality and varied samples in a small number of steps. Experiments show competitive results compared to the samples generated with a basic Generative Adversarial Net

A Cheap Linear Attention Mechanism with Fast Lookups and Fixed-Size Representations

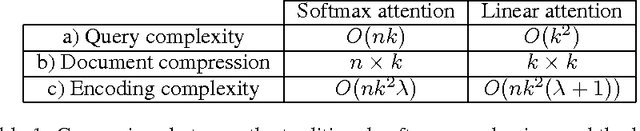
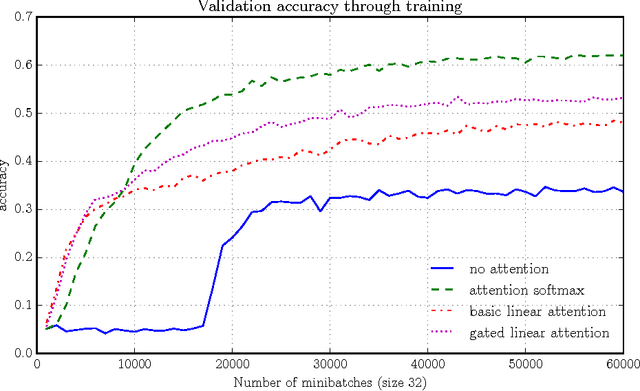
The softmax content-based attention mechanism has proven to be very beneficial in many applications of recurrent neural networks. Nevertheless it suffers from two major computational limitations. First, its computations for an attention lookup scale linearly in the size of the attended sequence. Second, it does not encode the sequence into a fixed-size representation but instead requires to memorize all the hidden states. These two limitations restrict the use of the softmax attention mechanism to relatively small-scale applications with short sequences and few lookups per sequence. In this work we introduce a family of linear attention mechanisms designed to overcome the two limitations listed above. We show that removing the softmax non-linearity from the traditional attention formulation yields constant-time attention lookups and fixed-size representations of the attended sequences. These properties make these linear attention mechanisms particularly suitable for large-scale applications with extreme query loads, real-time requirements and memory constraints. Early experiments on a question answering task show that these linear mechanisms yield significantly better accuracy results than no attention, but obviously worse than their softmax alternative.

Exact gradient updates in time independent of output size for the spherical loss family

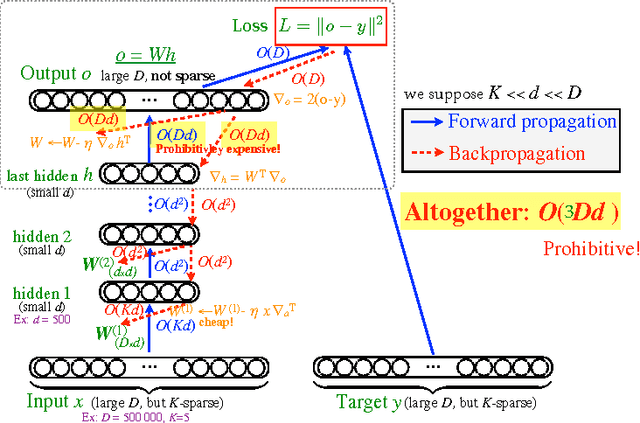
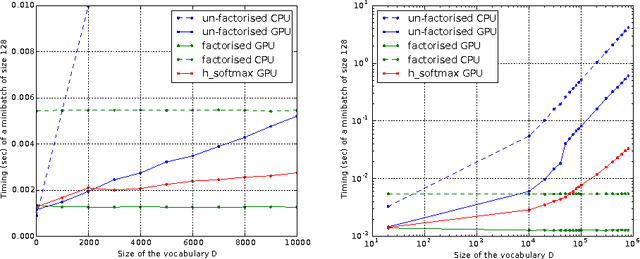
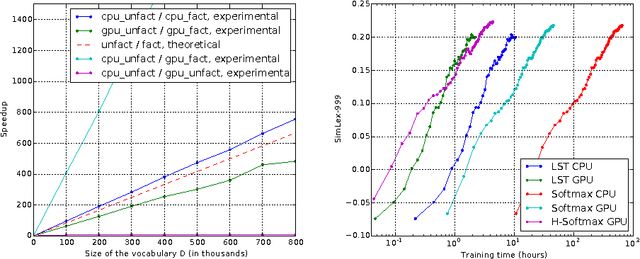
An important class of problems involves training deep neural networks with sparse prediction targets of very high dimension D. These occur naturally in e.g. neural language models or the learning of word-embeddings, often posed as predicting the probability of next words among a vocabulary of size D (e.g. 200,000). Computing the equally large, but typically non-sparse D-dimensional output vector from a last hidden layer of reasonable dimension d (e.g. 500) incurs a prohibitive O(Dd) computational cost for each example, as does updating the $D \times d$ output weight matrix and computing the gradient needed for backpropagation to previous layers. While efficient handling of large sparse network inputs is trivial, the case of large sparse targets is not, and has thus so far been sidestepped with approximate alternatives such as hierarchical softmax or sampling-based approximations during training. In this work we develop an original algorithmic approach which, for a family of loss functions that includes squared error and spherical softmax, can compute the exact loss, gradient update for the output weights, and gradient for backpropagation, all in $O(d^{2})$ per example instead of $O(Dd)$, remarkably without ever computing the D-dimensional output. The proposed algorithm yields a speedup of up to $D/4d$ i.e. two orders of magnitude for typical sizes, for that critical part of the computations that often dominates the training time in this kind of network architecture.

The Z-loss: a shift and scale invariant classification loss belonging to the Spherical Family

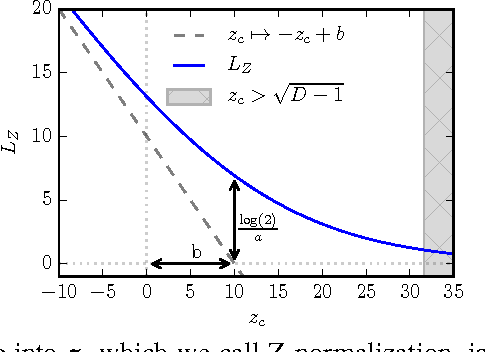
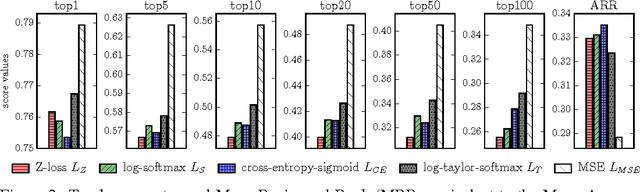
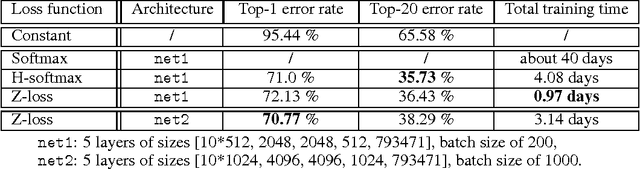
Despite being the standard loss function to train multi-class neural networks, the log-softmax has two potential limitations. First, it involves computations that scale linearly with the number of output classes, which can restrict the size of problems we are able to tackle with current hardware. Second, it remains unclear how close it matches the task loss such as the top-k error rate or other non-differentiable evaluation metrics which we aim to optimize ultimately. In this paper, we introduce an alternative classification loss function, the Z-loss, which is designed to address these two issues. Unlike the log-softmax, it has the desirable property of belonging to the spherical loss family (Vincent et al., 2015), a class of loss functions for which training can be performed very efficiently with a complexity independent of the number of output classes. We show experimentally that it significantly outperforms the other spherical loss functions previously investigated. Furthermore, we show on a word language modeling task that it also outperforms the log-softmax with respect to certain ranking scores, such as top-k scores, suggesting that the Z-loss has the flexibility to better match the task loss. These qualities thus makes the Z-loss an appealing candidate to train very efficiently large output networks such as word-language models or other extreme classification problems. On the One Billion Word (Chelba et al., 2014) dataset, we are able to train a model with the Z-loss 40 times faster than the log-softmax and more than 4 times faster than the hierarchical softmax.