Localized Persistent Homologies for more Effective Deep Learning

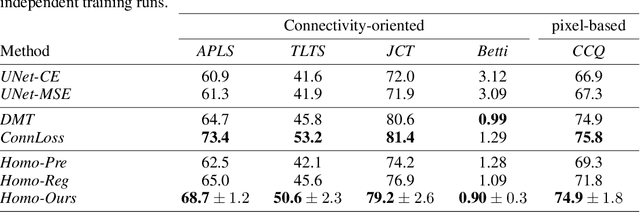
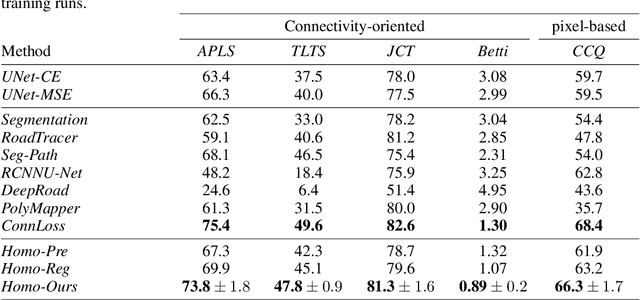
Persistent Homologies have been successfully used to increase the performance of deep networks trained to detect curvilinear structures and to improve the topological quality of the results. However, existing methods are very global and ignore the location of topological features. In this paper, we introduce an approach that relies on a new filtration function to account for location during network training. We demonstrate experimentally on 2D images of roads and 3D image stacks of neuronal processes that networks trained in this manner are better at recovering the topology of the curvilinear structures they extract.

DEBOSH: Deep Bayesian Shape Optimization

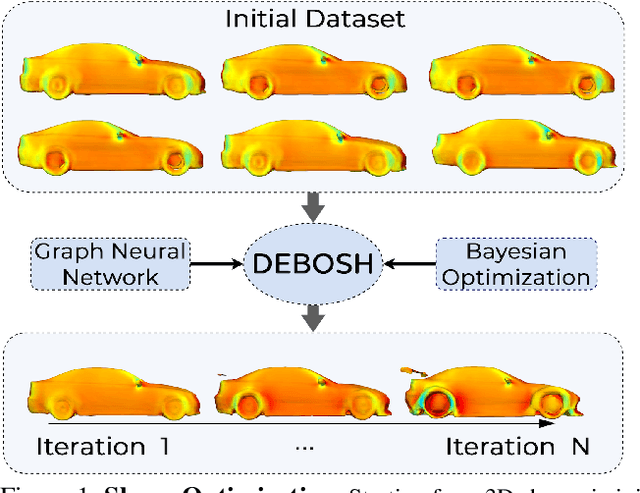
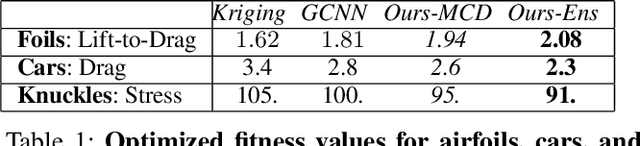
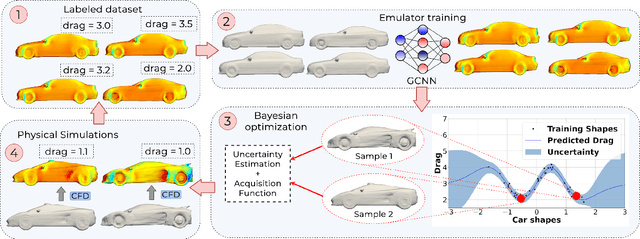
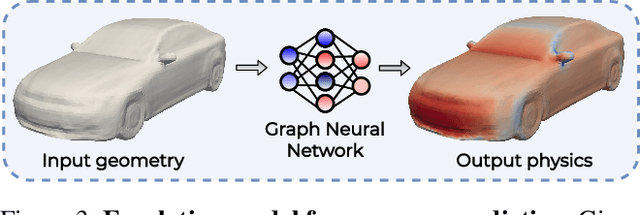
Shape optimization is at the heart of many industrial applications, such as aerodynamics, heat transfer, and structural analysis. It has recently been shown that Graph Neural Networks (GNNs) can predict the performance of a shape quickly and accurately and be used to optimize more effectively than traditional techniques that rely on response-surfaces obtained by Kriging. However, GNNs suffer from the fact that they do not evaluate their own accuracy, which is something Bayesian Optimization methods require. Therefore, estimating confidence in generated predictions is necessary to go beyond straight deterministic optimization, which is less effective. In this paper, we demonstrate that we can use Ensembles-based technique to overcome this limitation and outperform the state-of-the-art. Our experiments on diverse aerodynamics and structural analysis tasks prove that adding uncertainty to shape optimization significantly improves the quality of resulting shapes and reduces the time required for the optimization.

HybridSDF: Combining Free Form Shapes and Geometric Primitives for effective Shape Manipulation

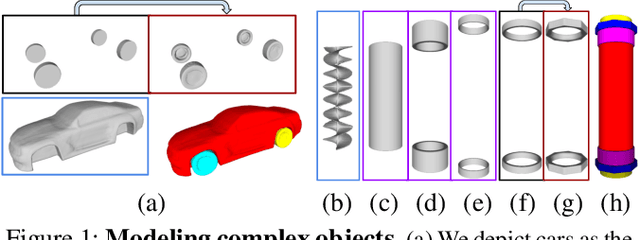
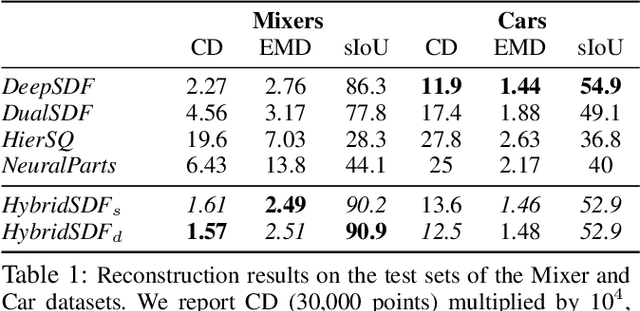
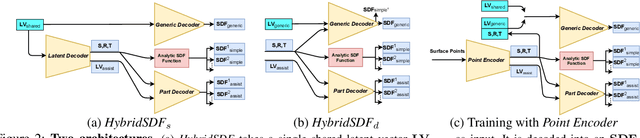
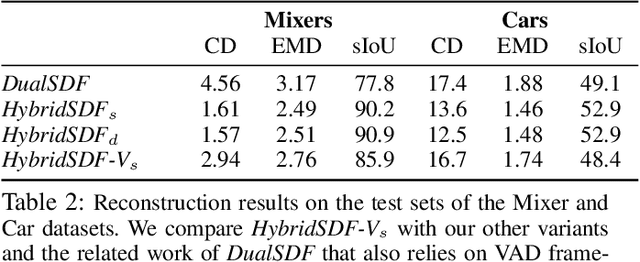
CAD modeling typically involves the use of simple geometric primitives whereas recent advances in deep-learning based 3D surface modeling have opened new shape design avenues. Unfortunately, these advances have not yet been accepted by the CAD community because they cannot be integrated into engineering workflows. To remedy this, we propose a novel approach to effectively combining geometric primitives and free-form surfaces represented by implicit surfaces for accurate modeling that preserves interpretability, enforces consistency, and enables easy manipulation.

DeepMesh: Differentiable Iso-Surface Extraction

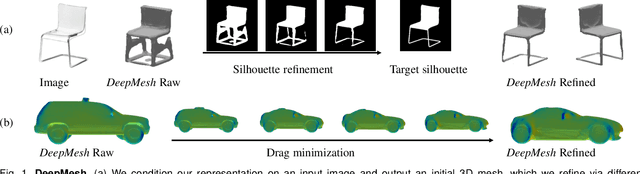
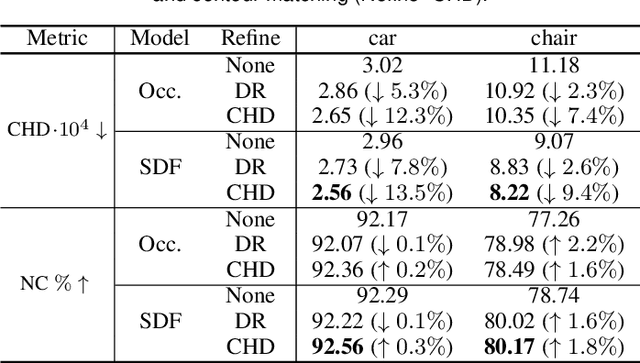
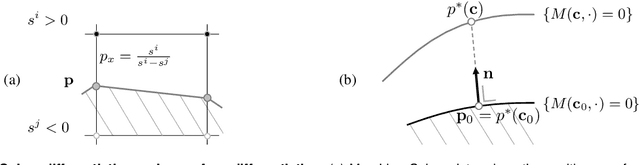
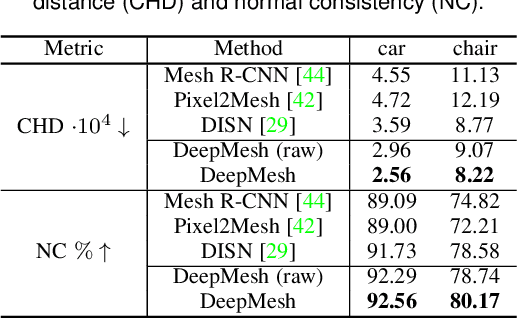
Geometric Deep Learning has recently made striking progress with the advent of continuous Deep Implicit Fields. They allow for detailed modeling of watertight surfaces of arbitrary topology while not relying on a 3D Euclidean grid, resulting in a learnable parameterization that is unlimited in resolution. Unfortunately, these methods are often unsuitable for applications that require an explicit mesh-based surface representation because converting an implicit field to such a representation relies on the Marching Cubes algorithm, which cannot be differentiated with respect to the underlying implicit field. In this work, we remove this limitation and introduce a differentiable way to produce explicit surface mesh representations from Deep Implicit Fields. Our key insight is that by reasoning on how implicit field perturbations impact local surface geometry, one can ultimately differentiate the 3D location of surface samples with respect to the underlying deep implicit field. We exploit this to define DeepMesh -- end-to-end differentiable mesh representation that can vary its topology. We use two different applications to validate our theoretical insight: Single view 3D Reconstruction via Differentiable Rendering and Physically-Driven Shape Optimization. In both cases our end-to-end differentiable parameterization gives us an edge over state-of-the-art algorithms.

Weakly Supervised Volumetric Image Segmentation with Deformed Templates

There are many approaches that use weak-supervision to train networks to segment 2D images. By contrast, existing 3D approaches rely on full-supervision of a subset of 2D slices of the 3D image volume. In this paper, we propose an approach that is truly weakly-supervised in the sense that we only need to provide a sparse set of 3D point on the surface of target objects, an easy task that can be quickly done. We use the 3D points to deform a 3D template so that it roughly matches the target object outlines and we introduce an architecture that exploits the supervision provided by coarse template to train a network to find accurate boundaries. We evaluate the performance of our approach on Computed Tomography (CT), Magnetic Resonance Imagery (MRI) and Electron Microscopy (EM) image datasets. We will show that it outperforms a more traditional approach to weak-supervision in 3D at a reduced supervision cost.

SegmentMeIfYouCan: A Benchmark for Anomaly Segmentation

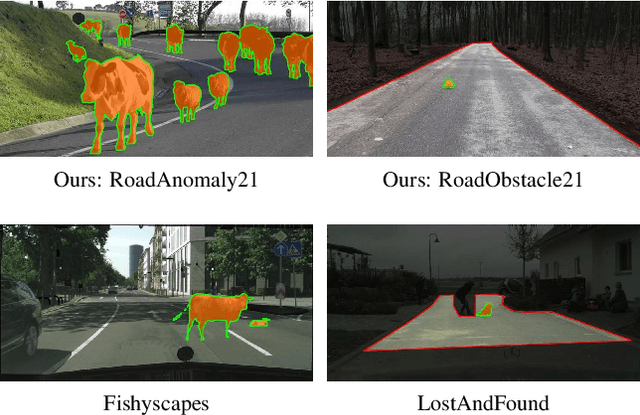
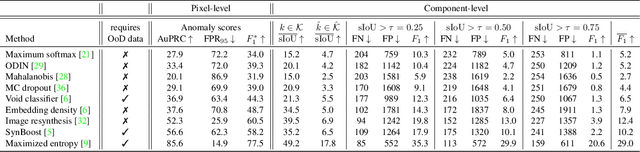
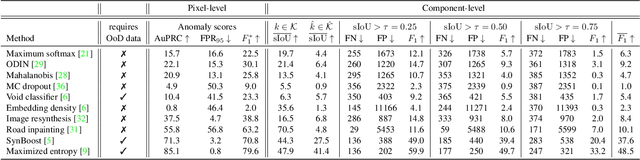
State-of-the-art semantic or instance segmentation deep neural networks (DNNs) are usually trained on a closed set of semantic classes. As such, they are ill-equipped to handle previously-unseen objects. However, detecting and localizing such objects is crucial for safety-critical applications such as perception for automated driving, especially if they appear on the road ahead. While some methods have tackled the tasks of anomalous or out-of-distribution object segmentation, progress remains slow, in large part due to the lack of solid benchmarks; existing datasets either consist of synthetic data, or suffer from label inconsistencies. In this paper, we bridge this gap by introducing the "SegmentMeIfYouCan" benchmark. Our benchmark addresses two tasks: Anomalous object segmentation, which considers any previously-unseen object category; and road obstacle segmentation, which focuses on any object on the road, may it be known or unknown. We provide two corresponding datasets together with a test suite performing an in-depth method analysis, considering both established pixel-wise performance metrics and recent component-wise ones, which are insensitive to object sizes. We empirically evaluate multiple state-of-the-art baseline methods, including several specifically designed for anomaly / obstacle segmentation, on our datasets as well as on public ones, using our benchmark suite. The anomaly and obstacle segmentation results show that our datasets contribute to the diversity and challengingness of both dataset landscapes.

Domain Adaptation for Semantic Segmentation via Patch-Wise Contrastive Learning

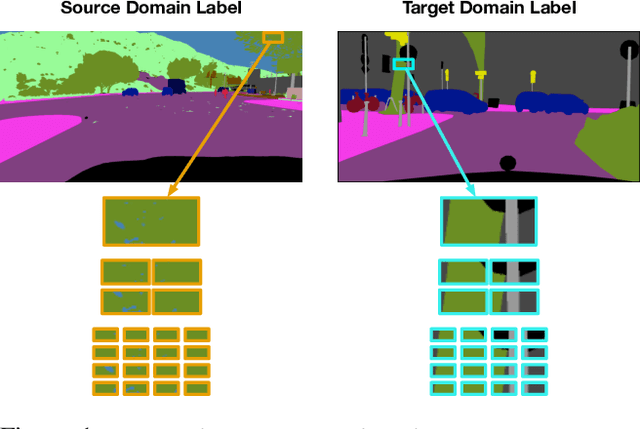
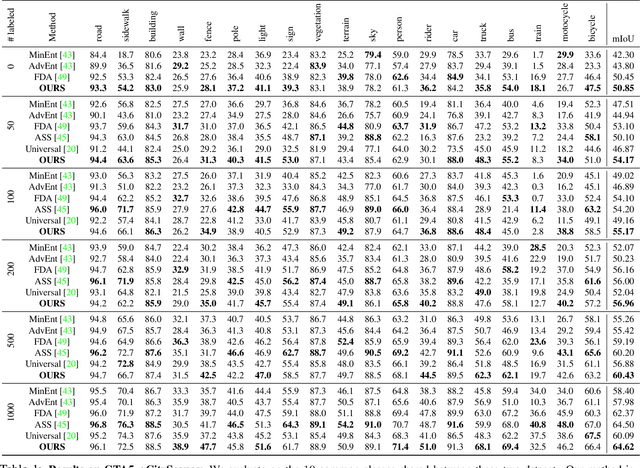
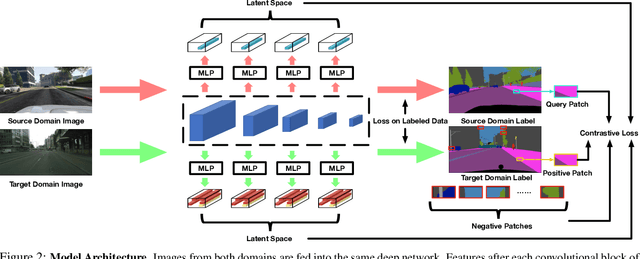
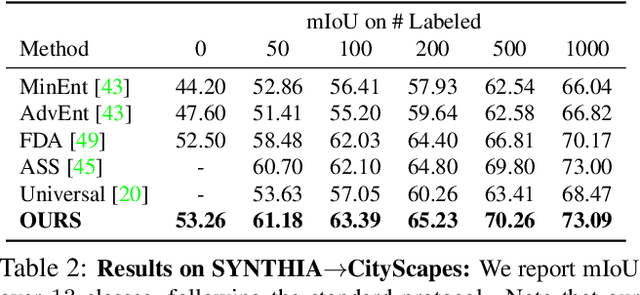
We introduce a novel approach to unsupervised and semi-supervised domain adaptation for semantic segmentation. Unlike many earlier methods that rely on adversarial learning for feature alignment, we leverage contrastive learning to bridge the domain gap by aligning the features of structurally similar label patches across domains. As a result, the networks are easier to train and deliver better performance. Our approach consistently outperforms state-of-the-art unsupervised and semi-supervised methods on two challenging domain adaptive segmentation tasks, particularly with a small number of target domain annotations. It can also be naturally extended to weakly-supervised domain adaptation, where only a minor drop in accuracy can save up to 75% of annotation cost.

Temporally-Coherent Surface Reconstruction via Metric-Consistent Atlases

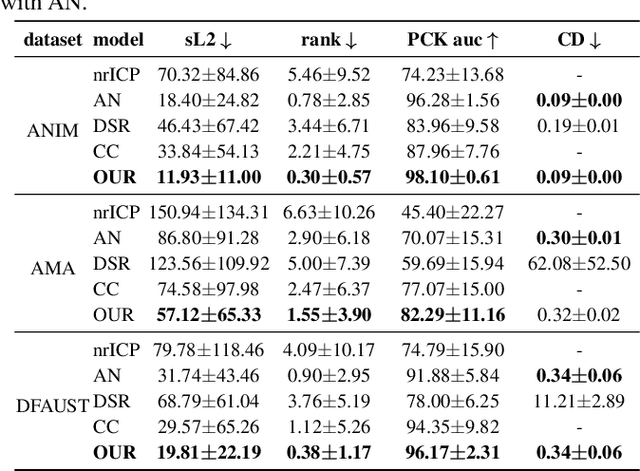
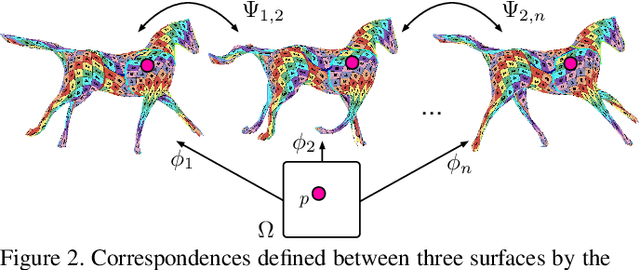
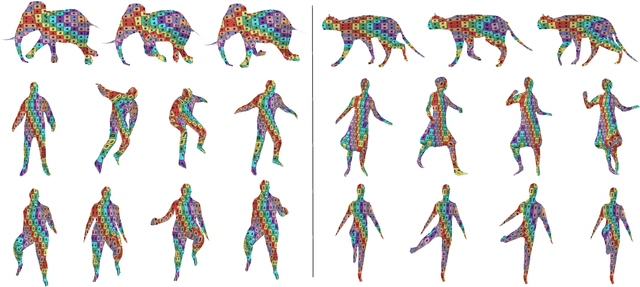
We propose a method for the unsupervised reconstruction of a temporally-coherent sequence of surfaces from a sequence of time-evolving point clouds, yielding dense, semantically meaningful correspondences between all keyframes. We represent the reconstructed surface as an atlas, using a neural network. Using canonical correspondences defined via the atlas, we encourage the reconstruction to be as isometric as possible across frames, leading to semantically-meaningful reconstruction. Through experiments and comparisons, we empirically show that our method achieves results that exceed that state of the art in the accuracy of unsupervised correspondences and accuracy of surface reconstruction.

Robust Differentiable SVD

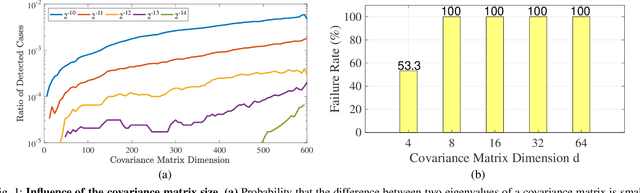
Eigendecomposition of symmetric matrices is at the heart of many computer vision algorithms. However, the derivatives of the eigenvectors tend to be numerically unstable, whether using the SVD to compute them analytically or using the Power Iteration (PI) method to approximate them. This instability arises in the presence of eigenvalues that are close to each other. This makes integrating eigendecomposition into deep networks difficult and often results in poor convergence, particularly when dealing with large matrices. While this can be mitigated by partitioning the data into small arbitrary groups, doing so has no theoretical basis and makes it impossible to exploit the full power of eigendecomposition. In previous work, we mitigated this using SVD during the forward pass and PI to compute the gradients during the backward pass. However, the iterative deflation procedure required to compute multiple eigenvectors using PI tends to accumulate errors and yield inaccurate gradients. Here, we show that the Taylor expansion of the SVD gradient is theoretically equivalent to the gradient obtained using PI without relying in practice on an iterative process and thus yields more accurate gradients. We demonstrate the benefits of this increased accuracy for image classification and style transfer.

Sketch2Mesh: Reconstructing and Editing 3D Shapes from Sketches

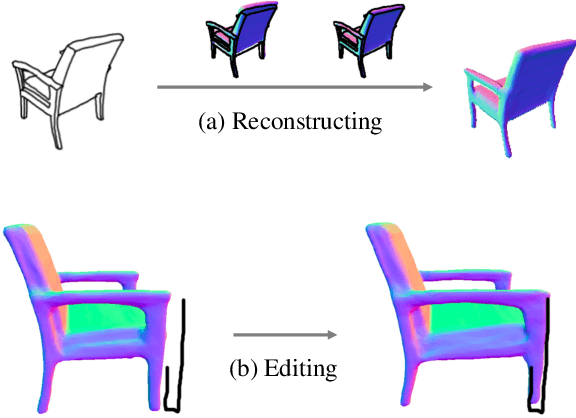
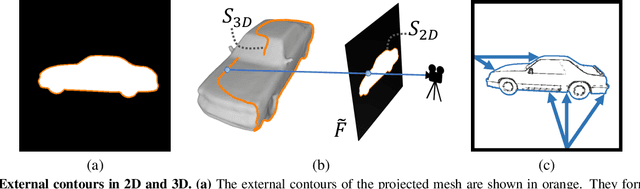
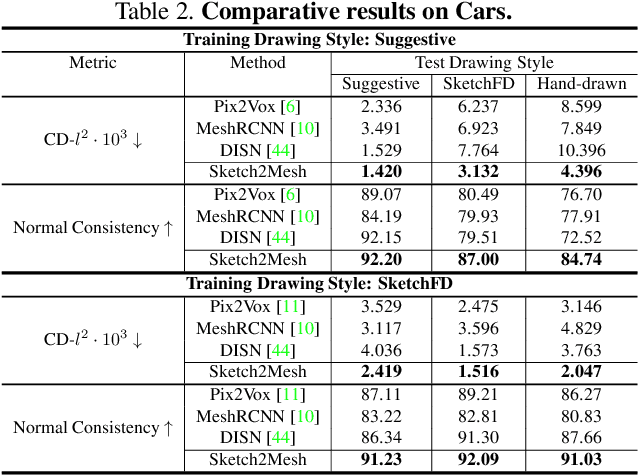
Reconstructing 3D shape from 2D sketches has long been an open problem because the sketches only provide very sparse and ambiguous information. In this paper, we use an encoder/decoder architecture for the sketch to mesh translation. This enables us to leverage its latent parametrization to represent and refine a 3D mesh so that its projections match the external contours outlined in the sketch. We will show that this approach is easy to deploy, robust to style changes, and effective. Furthermore, it can be used for shape refinement given only single pen strokes. We compare our approach to state-of-the-art methods on sketches -- both hand-drawn and synthesized -- and demonstrate that we outperform them.