BOFormer: Learning to Solve Multi-Objective Bayesian Optimization via Non-Markovian RL

Bayesian optimization (BO) offers an efficient pipeline for optimizing black-box functions with the help of a Gaussian process prior and an acquisition function (AF). Recently, in the context of single-objective BO, learning-based AFs witnessed promising empirical results given its favorable non-myopic nature. Despite this, the direct extension of these approaches to multi-objective Bayesian optimization (MOBO) suffer from the \textit{hypervolume identifiability issue}, which results from the non-Markovian nature of MOBO problems. To tackle this, inspired by the non-Markovian RL literature and the success of Transformers in language modeling, we present a generalized deep Q-learning framework and propose \textit{BOFormer}, which substantiates this framework for MOBO via sequence modeling. Through extensive evaluation, we demonstrate that BOFormer constantly outperforms the benchmark rule-based and learning-based algorithms in various synthetic MOBO and real-world multi-objective hyperparameter optimization problems. We have made the source code publicly available to encourage further research in this direction.

Value-Biased Maximum Likelihood Estimation for Model-based Reinforcement Learning in Discounted Linear MDPs

We consider the infinite-horizon linear Markov Decision Processes (MDPs), where the transition probabilities of the dynamic model can be linearly parameterized with the help of a predefined low-dimensional feature mapping. While the existing regression-based approaches have been theoretically shown to achieve nearly-optimal regret, they are computationally rather inefficient due to the need for a large number of optimization runs in each time step, especially when the state and action spaces are large. To address this issue, we propose to solve linear MDPs through the lens of Value-Biased Maximum Likelihood Estimation (VBMLE), which is a classic model-based exploration principle in the adaptive control literature for resolving the well-known closed-loop identification problem of Maximum Likelihood Estimation. We formally show that (i) VBMLE enjoys $\widetilde{O}(d\sqrt{T})$ regret, where $T$ is the time horizon and $d$ is the dimension of the model parameter, and (ii) VBMLE is computationally more efficient as it only requires solving one optimization problem in each time step. In our regret analysis, we offer a generic convergence result of MLE in linear MDPs through a novel supermartingale construct and uncover an interesting connection between linear MDPs and online learning, which could be of independent interest. Finally, the simulation results show that VBMLE significantly outperforms the benchmark method in terms of both empirical regret and computation time.

Neural Contextual Bandits via Reward-Biased Maximum Likelihood Estimation

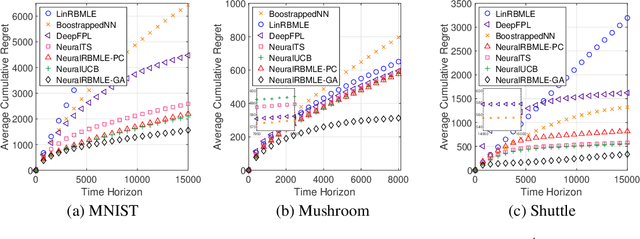
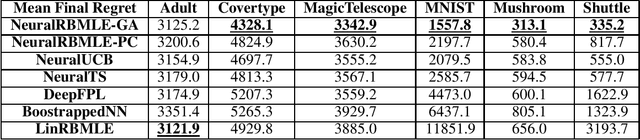
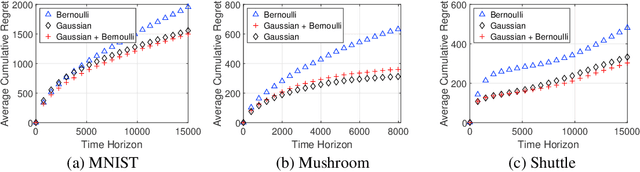
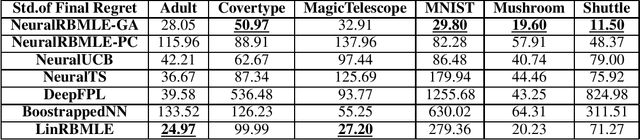
Reward-biased maximum likelihood estimation (RBMLE) is a classic principle in the adaptive control literature for tackling explore-exploit trade-offs. This paper studies the stochastic contextual bandit problem with general bounded reward functions and proposes NeuralRBMLE, which adapts the RBMLE principle by adding a bias term to the log-likelihood to enforce exploration. NeuralRBMLE leverages the representation power of neural networks and directly encodes exploratory behavior in the parameter space, without constructing confidence intervals of the estimated rewards. We propose two variants of NeuralRBMLE algorithms: The first variant directly obtains the RBMLE estimator by gradient ascent, and the second variant simplifies RBMLE to a simple index policy through an approximation. We show that both algorithms achieve $\widetilde{\mathcal{O}}(\sqrt{T})$ regret. Through extensive experiments, we demonstrate that the NeuralRBMLE algorithms achieve comparable or better empirical regrets than the state-of-the-art methods on real-world datasets with non-linear reward functions.

Reward-Biased Maximum Likelihood Estimation for Linear Stochastic Bandits

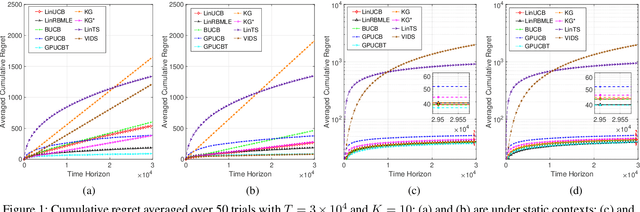
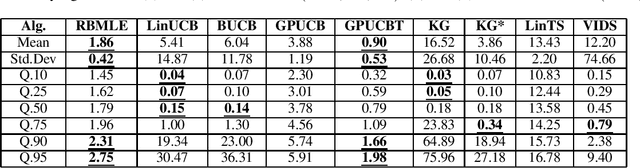
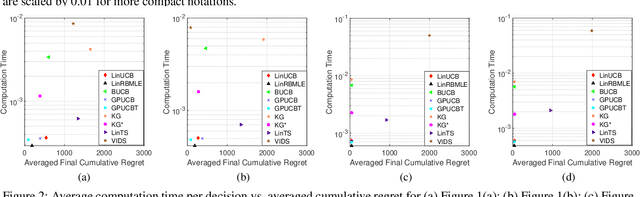
Modifying the reward-biased maximum likelihood method originally proposed in the adaptive control literature, we propose novel learning algorithms to handle the explore-exploit trade-off in linear bandits problems as well as generalized linear bandits problems. We develop novel index policies that we prove achieve order-optimality, and show that they achieve empirical performance competitive with the state-of-the-art benchmark methods in extensive experiments. The new policies achieve this with low computation time per pull for linear bandits, and thereby resulting in both favorable regret as well as computational efficiency.