A Topological Perspective on Demystifying GNN-Based Link Prediction Performance

Graph Neural Networks (GNNs) have shown great promise in learning node embeddings for link prediction (LP). While numerous studies aim to improve the overall LP performance of GNNs, none have explored its varying performance across different nodes and its underlying reasons. To this end, we aim to demystify which nodes will perform better from the perspective of their local topology. Despite the widespread belief that low-degree nodes exhibit poorer LP performance, our empirical findings provide nuances to this viewpoint and prompt us to propose a better metric, Topological Concentration (TC), based on the intersection of the local subgraph of each node with the ones of its neighbors. We empirically demonstrate that TC has a higher correlation with LP performance than other node-level topological metrics like degree and subgraph density, offering a better way to identify low-performing nodes than using cold-start. With TC, we discover a novel topological distribution shift issue in which newly joined neighbors of a node tend to become less interactive with that node's existing neighbors, compromising the generalizability of node embeddings for LP at testing time. To make the computation of TC scalable, We further propose Approximated Topological Concentration (ATC) and theoretically/empirically justify its efficacy in approximating TC and reducing the computation complexity. Given the positive correlation between node TC and its LP performance, we explore the potential of boosting LP performance via enhancing TC by re-weighting edges in the message-passing and discuss its effectiveness with limitations. Our code is publicly available at https://github.com/YuWVandy/Topo_LP_GNN.

Revisiting Link Prediction: A Data Perspective

Link prediction, a fundamental task on graphs, has proven indispensable in various applications, e.g., friend recommendation, protein analysis, and drug interaction prediction. However, since datasets span a multitude of domains, they could have distinct underlying mechanisms of link formation. Evidence in existing literature underscores the absence of a universally best algorithm suitable for all datasets. In this paper, we endeavor to explore principles of link prediction across diverse datasets from a data-centric perspective. We recognize three fundamental factors critical to link prediction: local structural proximity, global structural proximity, and feature proximity. We then unearth relationships among those factors where (i) global structural proximity only shows effectiveness when local structural proximity is deficient. (ii) The incompatibility can be found between feature and structural proximity. Such incompatibility leads to GNNs for Link Prediction (GNN4LP) consistently underperforming on edges where the feature proximity factor dominates. Inspired by these new insights from a data perspective, we offer practical instruction for GNN4LP model design and guidelines for selecting appropriate benchmark datasets for more comprehensive evaluations.

GraphPatcher: Mitigating Degree Bias for Graph Neural Networks via Test-time Augmentation

Recent studies have shown that graph neural networks (GNNs) exhibit strong biases towards the node degree: they usually perform satisfactorily on high-degree nodes with rich neighbor information but struggle with low-degree nodes. Existing works tackle this problem by deriving either designated GNN architectures or training strategies specifically for low-degree nodes. Though effective, these approaches unintentionally create an artificial out-of-distribution scenario, where models mainly or even only observe low-degree nodes during the training, leading to a downgraded performance for high-degree nodes that GNNs originally perform well at. In light of this, we propose a test-time augmentation framework, namely GraphPatcher, to enhance test-time generalization of any GNNs on low-degree nodes. Specifically, GraphPatcher iteratively generates virtual nodes to patch artificially created low-degree nodes via corruptions, aiming at progressively reconstructing target GNN's predictions over a sequence of increasingly corrupted nodes. Through this scheme, GraphPatcher not only learns how to enhance low-degree nodes (when the neighborhoods are heavily corrupted) but also preserves the original superior performance of GNNs on high-degree nodes (when lightly corrupted). Additionally, GraphPatcher is model-agnostic and can also mitigate the degree bias for either self-supervised or supervised GNNs. Comprehensive experiments are conducted over seven benchmark datasets and GraphPatcher consistently enhances common GNNs' overall performance by up to 3.6% and low-degree performance by up to 6.5%, significantly outperforming state-of-the-art baselines. The source code is publicly available at https://github.com/jumxglhf/GraphPatcher.

RobustL2S: Speaker-Specific Lip-to-Speech Synthesis exploiting Self-Supervised Representations

Significant progress has been made in speaker dependent Lip-to-Speech synthesis, which aims to generate speech from silent videos of talking faces. Current state-of-the-art approaches primarily employ non-autoregressive sequence-to-sequence architectures to directly predict mel-spectrograms or audio waveforms from lip representations. We hypothesize that the direct mel-prediction hampers training/model efficiency due to the entanglement of speech content with ambient information and speaker characteristics. To this end, we propose RobustL2S, a modularized framework for Lip-to-Speech synthesis. First, a non-autoregressive sequence-to-sequence model maps self-supervised visual features to a representation of disentangled speech content. A vocoder then converts the speech features into raw waveforms. Extensive evaluations confirm the effectiveness of our setup, achieving state-of-the-art performance on the unconstrained Lip2Wav dataset and the constrained GRID and TCD-TIMIT datasets. Speech samples from RobustL2S can be found at https://neha-sherin.github.io/RobustL2S/

Evaluating Graph Neural Networks for Link Prediction: Current Pitfalls and New Benchmarking

Link prediction attempts to predict whether an unseen edge exists based on only a portion of edges of a graph. A flurry of methods have been introduced in recent years that attempt to make use of graph neural networks (GNNs) for this task. Furthermore, new and diverse datasets have also been created to better evaluate the effectiveness of these new models. However, multiple pitfalls currently exist that hinder our ability to properly evaluate these new methods. These pitfalls mainly include: (1) Lower than actual performance on multiple baselines, (2) A lack of a unified data split and evaluation metric on some datasets, and (3) An unrealistic evaluation setting that uses easy negative samples. To overcome these challenges, we first conduct a fair comparison across prominent methods and datasets, utilizing the same dataset and hyperparameter search settings. We then create a more practical evaluation setting based on a Heuristic Related Sampling Technique (HeaRT), which samples hard negative samples via multiple heuristics. The new evaluation setting helps promote new challenges and opportunities in link prediction by aligning the evaluation with real-world situations. Our implementation and data are available at https://github.com/Juanhui28/HeaRT

CARL-G: Clustering-Accelerated Representation Learning on Graphs

Self-supervised learning on graphs has made large strides in achieving great performance in various downstream tasks. However, many state-of-the-art methods suffer from a number of impediments, which prevent them from realizing their full potential. For instance, contrastive methods typically require negative sampling, which is often computationally costly. While non-contrastive methods avoid this expensive step, most existing methods either rely on overly complex architectures or dataset-specific augmentations. In this paper, we ask: Can we borrow from classical unsupervised machine learning literature in order to overcome those obstacles? Guided by our key insight that the goal of distance-based clustering closely resembles that of contrastive learning: both attempt to pull representations of similar items together and dissimilar items apart. As a result, we propose CARL-G - a novel clustering-based framework for graph representation learning that uses a loss inspired by Cluster Validation Indices (CVIs), i.e., internal measures of cluster quality (no ground truth required). CARL-G is adaptable to different clustering methods and CVIs, and we show that with the right choice of clustering method and CVI, CARL-G outperforms node classification baselines on 4/5 datasets with up to a 79x training speedup compared to the best-performing baseline. CARL-G also performs at par or better than baselines in node clustering and similarity search tasks, training up to 1,500x faster than the best-performing baseline. Finally, we also provide theoretical foundations for the use of CVI-inspired losses in graph representation learning.

Demystifying Structural Disparity in Graph Neural Networks: Can One Size Fit All?

Recent studies on Graph Neural Networks(GNNs) provide both empirical and theoretical evidence supporting their effectiveness in capturing structural patterns on both homophilic and certain heterophilic graphs. Notably, most real-world homophilic and heterophilic graphs are comprised of a mixture of nodes in both homophilic and heterophilic structural patterns, exhibiting a structural disparity. However, the analysis of GNN performance with respect to nodes exhibiting different structural patterns, e.g., homophilic nodes in heterophilic graphs, remains rather limited. In the present study, we provide evidence that Graph Neural Networks(GNNs) on node classification typically perform admirably on homophilic nodes within homophilic graphs and heterophilic nodes within heterophilic graphs while struggling on the opposite node set, exhibiting a performance disparity. We theoretically and empirically identify effects of GNNs on testing nodes exhibiting distinct structural patterns. We then propose a rigorous, non-i.i.d PAC-Bayesian generalization bound for GNNs, revealing reasons for the performance disparity, namely the aggregated feature distance and homophily ratio difference between training and testing nodes. Furthermore, we demonstrate the practical implications of our new findings via (1) elucidating the effectiveness of deeper GNNs; and (2) revealing an over-looked distribution shift factor on graph out-of-distribution problem and proposing a new scenario accordingly.

MParrotTTS: Multilingual Multi-speaker Text to Speech Synthesis in Low Resource Setting

We present MParrotTTS, a unified multilingual, multi-speaker text-to-speech (TTS) synthesis model that can produce high-quality speech. Benefiting from a modularized training paradigm exploiting self-supervised speech representations, MParrotTTS adapts to a new language with minimal supervised data and generalizes to languages not seen while training the self-supervised backbone. Moreover, without training on any bilingual or parallel examples, MParrotTTS can transfer voices across languages while preserving the speaker-specific characteristics, e.g., synthesizing fluent Hindi speech using a French speaker's voice and accent. We present extensive results on six languages in terms of speech naturalness and speaker similarity in parallel and cross-lingual synthesis. The proposed model outperforms the state-of-the-art multilingual TTS models and baselines, using only a small fraction of supervised training data. Speech samples from our model can be found at https://paper2438.github.io/tts/

Link Prediction with Non-Contrastive Learning

A recent focal area in the space of graph neural networks (GNNs) is graph self-supervised learning (SSL), which aims to derive useful node representations without labeled data. Notably, many state-of-the-art graph SSL methods are contrastive methods, which use a combination of positive and negative samples to learn node representations. Owing to challenges in negative sampling (slowness and model sensitivity), recent literature introduced non-contrastive methods, which instead only use positive samples. Though such methods have shown promising performance in node-level tasks, their suitability for link prediction tasks, which are concerned with predicting link existence between pairs of nodes (and have broad applicability to recommendation systems contexts) is yet unexplored. In this work, we extensively evaluate the performance of existing non-contrastive methods for link prediction in both transductive and inductive settings. While most existing non-contrastive methods perform poorly overall, we find that, surprisingly, BGRL generally performs well in transductive settings. However, it performs poorly in the more realistic inductive settings where the model has to generalize to links to/from unseen nodes. We find that non-contrastive models tend to overfit to the training graph and use this analysis to propose T-BGRL, a novel non-contrastive framework that incorporates cheap corruptions to improve the generalization ability of the model. This simple modification strongly improves inductive performance in 5/6 of our datasets, with up to a 120% improvement in Hits@50--all with comparable speed to other non-contrastive baselines and up to 14x faster than the best-performing contrastive baseline. Our work imparts interesting findings about non-contrastive learning for link prediction and paves the way for future researchers to further expand upon this area.

Linkless Link Prediction via Relational Distillation

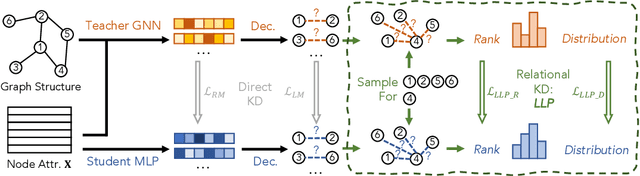
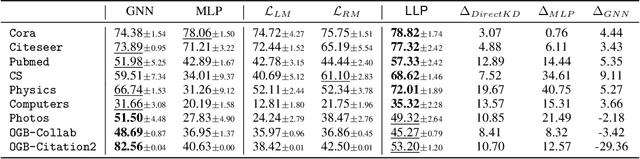
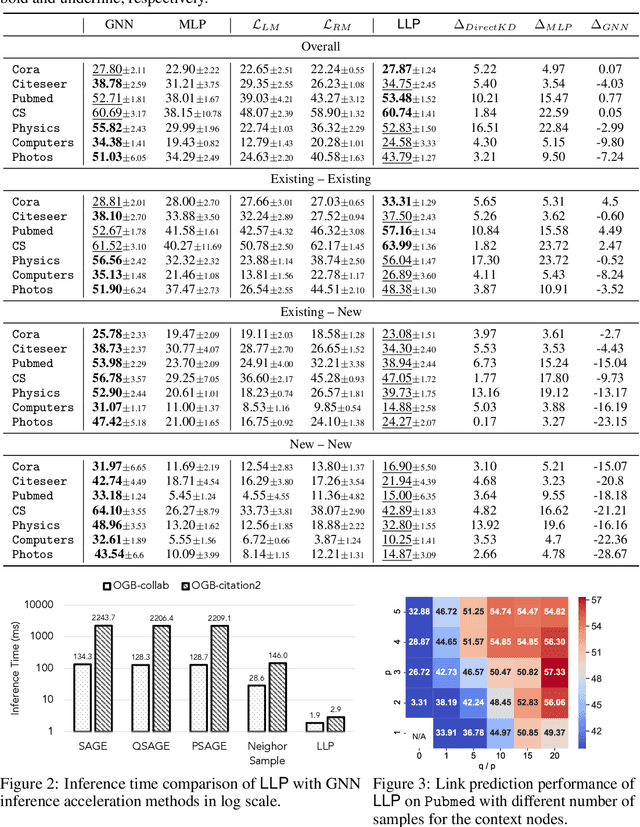
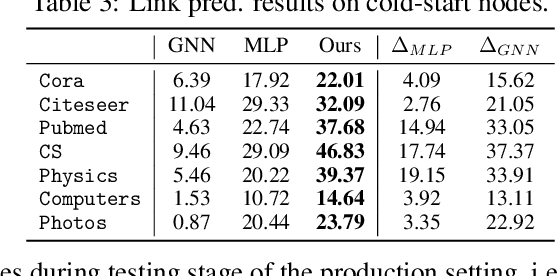
Graph Neural Networks (GNNs) have been widely used on graph data and have shown exceptional performance in the task of link prediction. Despite their effectiveness, GNNs often suffer from high latency due to non-trivial neighborhood data dependency in practical deployments. To address this issue, researchers have proposed methods based on knowledge distillation (KD) to transfer the knowledge from teacher GNNs to student MLPs, which are known to be efficient even with industrial scale data, and have shown promising results on node classification. Nonetheless, using KD to accelerate link prediction is still unexplored. In this work, we start with exploring two direct analogs of traditional KD for link prediction, i.e., predicted logit-based matching and node representation-based matching. Upon observing direct KD analogs do not perform well for link prediction, we propose a relational KD framework, Linkless Link Prediction (LLP). Unlike simple KD methods that match independent link logits or node representations, LLP distills relational knowledge that is centered around each (anchor) node to the student MLP. Specifically, we propose two matching strategies that complement each other: rank-based matching and distribution-based matching. Extensive experiments demonstrate that LLP boosts the link prediction performance of MLPs with significant margins, and even outperforms the teacher GNNs on 6 out of 9 benchmarks. LLP also achieves a 776.37x speedup in link prediction inference compared to GNNs on the large scale OGB-Citation2 dataset.