HELM: Hyperbolic Large Language Models via Mixture-of-Curvature Experts

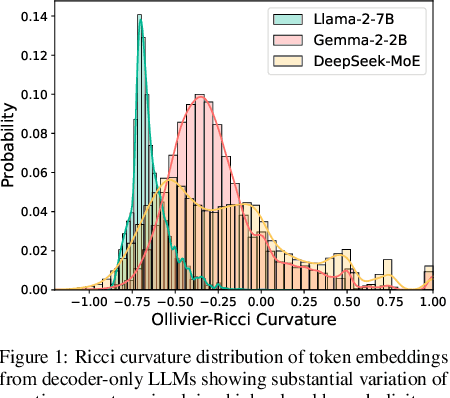
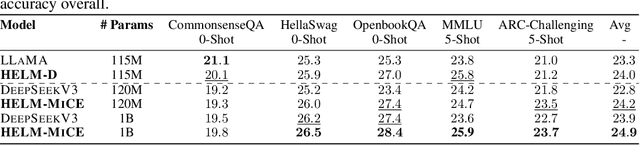
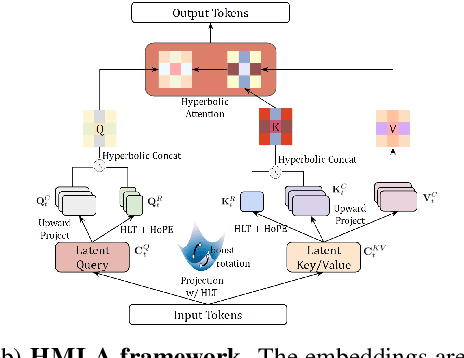
Large language models (LLMs) have shown great success in text modeling tasks across domains. However, natural language exhibits inherent semantic hierarchies and nuanced geometric structure, which current LLMs do not capture completely owing to their reliance on Euclidean operations. Recent studies have also shown that not respecting the geometry of token embeddings leads to training instabilities and degradation of generative capabilities. These findings suggest that shifting to non-Euclidean geometries can better align language models with the underlying geometry of text. We thus propose to operate fully in Hyperbolic space, known for its expansive, scale-free, and low-distortion properties. We thus introduce HELM, a family of HypErbolic Large Language Models, offering a geometric rethinking of the Transformer-based LLM that addresses the representational inflexibility, missing set of necessary operations, and poor scalability of existing hyperbolic LMs. We additionally introduce a Mixture-of-Curvature Experts model, HELM-MICE, where each expert operates in a distinct curvature space to encode more fine-grained geometric structure from text, as well as a dense model, HELM-D. For HELM-MICE, we further develop hyperbolic Multi-Head Latent Attention (HMLA) for efficient, reduced-KV-cache training and inference. For both models, we develop essential hyperbolic equivalents of rotary positional encodings and RMS normalization. We are the first to train fully hyperbolic LLMs at billion-parameter scale, and evaluate them on well-known benchmarks such as MMLU and ARC, spanning STEM problem-solving, general knowledge, and commonsense reasoning. Our results show consistent gains from our HELM architectures -- up to 4% -- over popular Euclidean architectures used in LLaMA and DeepSeek, highlighting the efficacy and enhanced reasoning afforded by hyperbolic geometry in large-scale LM pretraining.

Efficient Diffusion Models for Symmetric Manifolds

We introduce a framework for designing efficient diffusion models for $d$-dimensional symmetric-space Riemannian manifolds, including the torus, sphere, special orthogonal group and unitary group. Existing manifold diffusion models often depend on heat kernels, which lack closed-form expressions and require either $d$ gradient evaluations or exponential-in-$d$ arithmetic operations per training step. We introduce a new diffusion model for symmetric manifolds with a spatially-varying covariance, allowing us to leverage a projection of Euclidean Brownian motion to bypass heat kernel computations. Our training algorithm minimizes a novel efficient objective derived via Ito's Lemma, allowing each step to run in $O(1)$ gradient evaluations and nearly-linear-in-$d$ ($O(d^{1.19})$) arithmetic operations, reducing the gap between diffusions on symmetric manifolds and Euclidean space. Manifold symmetries ensure the diffusion satisfies an "average-case" Lipschitz condition, enabling accurate and efficient sample generation. Empirically, our model outperforms prior methods in training speed and improves sample quality on synthetic datasets on the torus, special orthogonal group, and unitary group.

HyperCore: The Core Framework for Building Hyperbolic Foundation Models with Comprehensive Modules

Hyperbolic neural networks have emerged as a powerful tool for modeling hierarchical data across diverse modalities. Recent studies show that token distributions in foundation models exhibit scale-free properties, suggesting that hyperbolic space is a more suitable ambient space than Euclidean space for many pre-training and downstream tasks. However, existing tools lack essential components for building hyperbolic foundation models, making it difficult to leverage recent advancements. We introduce HyperCore, a comprehensive open-source framework that provides core modules for constructing hyperbolic foundation models across multiple modalities. HyperCore's modules can be effortlessly combined to develop novel hyperbolic foundation models, eliminating the need to extensively modify Euclidean modules from scratch and possible redundant research efforts. To demonstrate its versatility, we build and test the first fully hyperbolic vision transformers (LViT) with a fine-tuning pipeline, the first fully hyperbolic multimodal CLIP model (L-CLIP), and a hybrid Graph RAG with a hyperbolic graph encoder. Our experiments demonstrate that LViT outperforms its Euclidean counterpart. Additionally, we benchmark and reproduce experiments across hyperbolic GNNs, CNNs, Transformers, and vision Transformers to highlight HyperCore's advantages.

Position: Beyond Euclidean -- Foundation Models Should Embrace Non-Euclidean Geometries

In the era of foundation models and Large Language Models (LLMs), Euclidean space has been the de facto geometric setting for machine learning architectures. However, recent literature has demonstrated that this choice comes with fundamental limitations. At a large scale, real-world data often exhibit inherently non-Euclidean structures, such as multi-way relationships, hierarchies, symmetries, and non-isotropic scaling, in a variety of domains, such as languages, vision, and the natural sciences. It is challenging to effectively capture these structures within the constraints of Euclidean spaces. This position paper argues that moving beyond Euclidean geometry is not merely an optional enhancement but a necessity to maintain the scaling law for the next-generation of foundation models. By adopting these geometries, foundation models could more efficiently leverage the aforementioned structures. Task-aware adaptability that dynamically reconfigures embeddings to match the geometry of downstream applications could further enhance efficiency and expressivity. Our position is supported by a series of theoretical and empirical investigations of prevalent foundation models.Finally, we outline a roadmap for integrating non-Euclidean geometries into foundation models, including strategies for building geometric foundation models via fine-tuning, training from scratch, and hybrid approaches.

Lorentzian Residual Neural Networks

Hyperbolic neural networks have emerged as a powerful tool for modeling hierarchical data structures prevalent in real-world datasets. Notably, residual connections, which facilitate the direct flow of information across layers, have been instrumental in the success of deep neural networks. However, current methods for constructing hyperbolic residual networks suffer from limitations such as increased model complexity, numerical instability, and errors due to multiple mappings to and from the tangent space. To address these limitations, we introduce LResNet, a novel Lorentzian residual neural network based on the weighted Lorentzian centroid in the Lorentz model of hyperbolic geometry. Our method enables the efficient integration of residual connections in Lorentz hyperbolic neural networks while preserving their hierarchical representation capabilities. We demonstrate that our method can theoretically derive previous methods while offering improved stability, efficiency, and effectiveness. Extensive experiments on both graph and vision tasks showcase the superior performance and robustness of our method compared to state-of-the-art Euclidean and hyperbolic alternatives. Our findings highlight the potential of \method for building more expressive neural networks in hyperbolic embedding space as a generally applicable method to multiple architectures, including CNNs, GNNs, and graph Transformers.