Efficient Diffusion Models for Symmetric Manifolds

We introduce a framework for designing efficient diffusion models for $d$-dimensional symmetric-space Riemannian manifolds, including the torus, sphere, special orthogonal group and unitary group. Existing manifold diffusion models often depend on heat kernels, which lack closed-form expressions and require either $d$ gradient evaluations or exponential-in-$d$ arithmetic operations per training step. We introduce a new diffusion model for symmetric manifolds with a spatially-varying covariance, allowing us to leverage a projection of Euclidean Brownian motion to bypass heat kernel computations. Our training algorithm minimizes a novel efficient objective derived via Ito's Lemma, allowing each step to run in $O(1)$ gradient evaluations and nearly-linear-in-$d$ ($O(d^{1.19})$) arithmetic operations, reducing the gap between diffusions on symmetric manifolds and Euclidean space. Manifold symmetries ensure the diffusion satisfies an "average-case" Lipschitz condition, enabling accurate and efficient sample generation. Empirically, our model outperforms prior methods in training speed and improves sample quality on synthetic datasets on the torus, special orthogonal group, and unitary group.

Private Low-Rank Approximation for Covariance Matrices, Dyson Brownian Motion, and Eigenvalue-Gap Bounds for Gaussian Perturbations

We consider the problem of approximating a $d \times d$ covariance matrix $M$ with a rank-$k$ matrix under $(\varepsilon,\delta)$-differential privacy. We present and analyze a complex variant of the Gaussian mechanism and obtain upper bounds on the Frobenius norm of the difference between the matrix output by this mechanism and the best rank-$k$ approximation to $M$. Our analysis provides improvements over previous bounds, particularly when the spectrum of $M$ satisfies natural structural assumptions. The novel insight is to view the addition of Gaussian noise to a matrix as a continuous-time matrix Brownian motion. This viewpoint allows us to track the evolution of eigenvalues and eigenvectors of the matrix, which are governed by stochastic differential equations discovered by Dyson. These equations enable us to upper bound the Frobenius distance between the best rank-$k$ approximation of $M$ and that of a Gaussian perturbation of $M$ as an integral that involves inverse eigenvalue gaps of the stochastically evolving matrix, as opposed to a sum of perturbation bounds obtained via Davis-Kahan-type theorems. Subsequently, again using the Dyson Brownian motion viewpoint, we show that the eigenvalues of the matrix $M$ perturbed by Gaussian noise have large gaps with high probability. These results also contribute to the analysis of low-rank approximations under average-case perturbations, and to an understanding of eigenvalue gaps for random matrices, both of which may be of independent interest.

Faster Sampling from Log-Concave Densities over Polytopes via Efficient Linear Solvers

We consider the problem of sampling from a log-concave distribution $\pi(\theta) \propto e^{-f(\theta)}$ constrained to a polytope $K:=\{\theta \in \mathbb{R}^d: A\theta \leq b\}$, where $A\in \mathbb{R}^{m\times d}$ and $b \in \mathbb{R}^m$.The fastest-known algorithm \cite{mangoubi2022faster} for the setting when $f$ is $O(1)$-Lipschitz or $O(1)$-smooth runs in roughly $O(md \times md^{\omega -1})$ arithmetic operations, where the $md^{\omega -1}$ term arises because each Markov chain step requires computing a matrix inversion and determinant (here $\omega \approx 2.37$ is the matrix multiplication constant). We present a nearly-optimal implementation of this Markov chain with per-step complexity which is roughly the number of non-zero entries of $A$ while the number of Markov chain steps remains the same. The key technical ingredients are 1) to show that the matrices that arise in this Dikin walk change slowly, 2) to deploy efficient linear solvers that can leverage this slow change to speed up matrix inversion by using information computed in previous steps, and 3) to speed up the computation of the determinantal term in the Metropolis filter step via a randomized Taylor series-based estimator.

Private Covariance Approximation and Eigenvalue-Gap Bounds for Complex Gaussian Perturbations

We consider the problem of approximating a $d \times d$ covariance matrix $M$ with a rank-$k$ matrix under $(\varepsilon,\delta)$-differential privacy. We present and analyze a complex variant of the Gaussian mechanism and show that the Frobenius norm of the difference between the matrix output by this mechanism and the best rank-$k$ approximation to $M$ is bounded by roughly $\tilde{O}(\sqrt{kd})$, whenever there is an appropriately large gap between the $k$'th and the $k+1$'th eigenvalues of $M$. This improves on previous work that requires that the gap between every pair of top-$k$ eigenvalues of $M$ is at least $\sqrt{d}$ for a similar bound. Our analysis leverages the fact that the eigenvalues of complex matrix Brownian motion repel more than in the real case, and uses Dyson's stochastic differential equations governing the evolution of its eigenvalues to show that the eigenvalues of the matrix $M$ perturbed by complex Gaussian noise have large gaps with high probability. Our results contribute to the analysis of low-rank approximations under average-case perturbations and to an understanding of eigenvalue gaps for random matrices, which may be of independent interest.

Re-Analyze Gauss: Bounds for Private Matrix Approximation via Dyson Brownian Motion

Given a symmetric matrix $M$ and a vector $\lambda$, we present new bounds on the Frobenius-distance utility of the Gaussian mechanism for approximating $M$ by a matrix whose spectrum is $\lambda$, under $(\varepsilon,\delta)$-differential privacy. Our bounds depend on both $\lambda$ and the gaps in the eigenvalues of $M$, and hold whenever the top $k+1$ eigenvalues of $M$ have sufficiently large gaps. When applied to the problems of private rank-$k$ covariance matrix approximation and subspace recovery, our bounds yield improvements over previous bounds. Our bounds are obtained by viewing the addition of Gaussian noise as a continuous-time matrix Brownian motion. This viewpoint allows us to track the evolution of eigenvalues and eigenvectors of the matrix, which are governed by stochastic differential equations discovered by Dyson. These equations allow us to bound the utility as the square-root of a sum-of-squares of perturbations to the eigenvectors, as opposed to a sum of perturbation bounds obtained via Davis-Kahan-type theorems.

Private Matrix Approximation and Geometry of Unitary Orbits

Consider the following optimization problem: Given $n \times n$ matrices $A$ and $\Lambda$, maximize $\langle A, U\Lambda U^*\rangle$ where $U$ varies over the unitary group $\mathrm{U}(n)$. This problem seeks to approximate $A$ by a matrix whose spectrum is the same as $\Lambda$ and, by setting $\Lambda$ to be appropriate diagonal matrices, one can recover matrix approximation problems such as PCA and rank-$k$ approximation. We study the problem of designing differentially private algorithms for this optimization problem in settings where the matrix $A$ is constructed using users' private data. We give efficient and private algorithms that come with upper and lower bounds on the approximation error. Our results unify and improve upon several prior works on private matrix approximation problems. They rely on extensions of packing/covering number bounds for Grassmannians to unitary orbits which should be of independent interest.

Faster Sampling from Log-Concave Distributions over Polytopes via a Soft-Threshold Dikin Walk

We consider the problem of sampling from a $d$-dimensional log-concave distribution $\pi(\theta) \propto e^{-f(\theta)}$ constrained to a polytope $K$ defined by $m$ inequalities. Our main result is a "soft-threshold'' variant of the Dikin walk Markov chain that requires at most $O((md + d L^2 R^2) \times md^{\omega-1}) \log(\frac{w}{\delta}))$ arithmetic operations to sample from $\pi$ within error $\delta>0$ in the total variation distance from a $w$-warm start, where $L$ is the Lipschitz-constant of $f$, $K$ is contained in a ball of radius $R$ and contains a ball of smaller radius $r$, and $\omega$ is the matrix-multiplication constant. When a warm start is not available, it implies an improvement of $\tilde{O}(d^{3.5-\omega})$ arithmetic operations on the previous best bound for sampling from $\pi$ within total variation error $\delta$, which was obtained with the hit-and-run algorithm, in the setting where $K$ is a polytope given by $m=O(d)$ inequalities and $LR = O(\sqrt{d})$. When a warm start is available, our algorithm improves by a factor of $d^2$ arithmetic operations on the best previous bound in this setting, which was obtained for a different version of the Dikin walk algorithm. Plugging our Dikin walk Markov chain into the post-processing algorithm of Mangoubi and Vishnoi (2021), we achieve further improvements in the dependence of the running time for the problem of generating samples from $\pi$ with infinity distance bounds in the special case when $K$ is a polytope.

Sampling from Log-Concave Distributions with Infinity-Distance Guarantees and Applications to Differentially Private Optimization

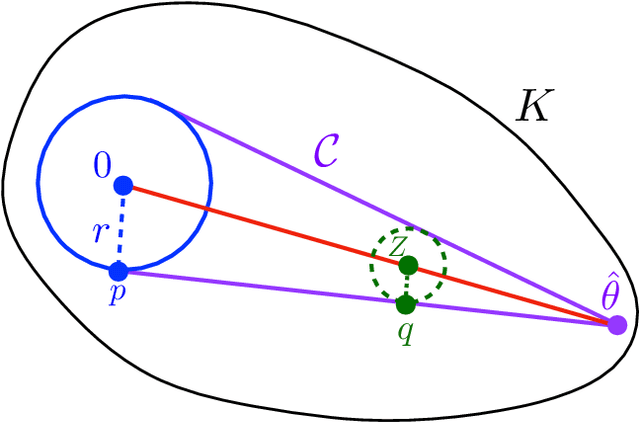
For a $d$-dimensional log-concave distribution $\pi(\theta)\propto e^{-f(\theta)}$ on a polytope $K$, we consider the problem of outputting samples from a distribution $\nu$ which is $O(\varepsilon)$-close in infinity-distance $\sup_{\theta\in K}|\log\frac{\nu(\theta)}{\pi(\theta)}|$ to $\pi$. Such samplers with infinity-distance guarantees are specifically desired for differentially private optimization as traditional sampling algorithms which come with total-variation distance or KL divergence bounds are insufficient to guarantee differential privacy. Our main result is an algorithm that outputs a point from a distribution $O(\varepsilon)$-close to $\pi$ in infinity-distance and requires $O((md+dL^2R^2)\times(LR+d\log(\frac{Rd+LRd}{\varepsilon r}))\times md^{\omega-1})$ arithmetic operations, where $f$ is $L$-Lipschitz, $K$ is defined by $m$ inequalities, is contained in a ball of radius $R$ and contains a ball of smaller radius $r$, and $\omega$ is the matrix-multiplication constant. In particular this runtime is logarithmic in $\frac{1}{\varepsilon}$ and significantly improves on prior works. Technically, we depart from the prior works that construct Markov chains on a $\frac{1}{\varepsilon^2}$-discretization of $K$ to achieve a sample with $O(\varepsilon)$ infinity-distance error, and present a method to convert continuous samples from $K$ with total-variation bounds to samples with infinity bounds. To achieve improved dependence on $d$, we present a "soft-threshold" version of the Dikin walk which may be of independent interest. Plugging our algorithm into the framework of the exponential mechanism yields similar improvements in the running time of $\varepsilon$-pure differentially private algorithms for optimization problems such as empirical risk minimization of Lipschitz-convex functions and low-rank approximation, while still achieving the tightest known utility bounds.

Sync-Switch: Hybrid Parameter Synchronization for Distributed Deep Learning

Stochastic Gradient Descent (SGD) has become the de facto way to train deep neural networks in distributed clusters. A critical factor in determining the training throughput and model accuracy is the choice of the parameter synchronization protocol. For example, while Bulk Synchronous Parallel (BSP) often achieves better converged accuracy, the corresponding training throughput can be negatively impacted by stragglers. In contrast, Asynchronous Parallel (ASP) can have higher throughput, but its convergence and accuracy can be impacted by stale gradients. To improve the performance of synchronization protocol, recent work often focuses on designing new protocols with a heavy reliance on hard-to-tune hyper-parameters. In this paper, we design a hybrid synchronization approach that exploits the benefits of both BSP and ASP, i.e., reducing training time while simultaneously maintaining the converged accuracy. Based on extensive empirical profiling, we devise a collection of adaptive policies that determine how and when to switch between synchronization protocols. Our policies include both offline ones that target recurring jobs and online ones for handling transient stragglers. We implement the proposed policies in a prototype system, called Sync-Switch, on top of TensorFlow, and evaluate the training performance with popular deep learning models and datasets. Our experiments show that Sync-Switch achieves up to 5.13X throughput speedup and similar converged accuracy when comparing to BSP. Further, we observe that Sync-Switch achieves 3.8% higher converged accuracy with just 1.23X the training time compared to training with ASP. Moreover, Sync-Switch can be used in settings when training with ASP leads to divergence errors. Sync-Switch achieves all of these benefits with very low overhead, e.g., the framework overhead can be as low as 1.7% of the total training time.

A Provably Convergent and Practical Algorithm for Min-max Optimization with Applications to GANs

We present a new algorithm for optimizing min-max loss functions that arise in training GANs. We prove that our algorithm converges to an equilibrium point in time polynomial in the dimension, and smoothness parameters of the loss function. The point our algorithm converges to is stable when the maximizing player can respond using any sequence of steps which increase the loss at each step, and the minimizing player is empowered to simulate the maximizing player's response for arbitrarily many steps but is restricted to move according to updates sampled from a stochastic gradient oracle. We apply our algorithm to train GANs on Gaussian mixtures, MNIST and CIFAR-10. We observe that our algorithm trains stably and avoids mode collapse, while achieving a training time per iteration and memory requirement similar to gradient descent-ascent.