Falsification of Autonomous Systems in Rich Environments

Validating the behavior of autonomous Cyber-Physical Systems (CPS) and Artificial Intelligence (AI) agents, which rely on automated controllers, is an objective of great importance. In recent years, Neural-Network (NN) controllers have been demonstrating great promise. Unfortunately, such learned controllers are often not certified and can cause the system to suffer from unpredictable or unsafe behavior. To mitigate this issue, a great effort has been dedicated to automated verification of systems. Specifically, works in the category of ``black-box testing'' rely on repeated system simulations to find a falsifying counterexample of a system run that violates a specification. As running high-fidelity simulations is computationally demanding, the goal of falsification approaches is to minimize the simulation effort (NN inference queries) needed to return a falsifying example. This often proves to be a great challenge, especially when the tested controller is well-trained. This work contributes a novel falsification approach for autonomous systems under formal specification operating in uncertain environments. We are especially interested in CPS operating in rich, semantically-defined, open environments, which yield high-dimensional, simulation-dependent sensor observations. Our approach introduces a novel reformulation of the falsification problem as the problem of planning a trajectory for a ``meta-system,'' which wraps and encapsulates the examined system; we call this approach: meta-planning. This formulation can be solved with standard sampling-based motion-planning techniques (like RRT) and can gradually integrate domain knowledge to improve the search. We support the suggested approach with an experimental study on falsification of an obstacle-avoiding autonomous car with a NN controller, where meta-planning demonstrates superior performance over alternative approaches.

LTLf Synthesis Under Unreliable Input

We study the problem of realizing strategies for an LTLf goal specification while ensuring that at least an LTLf backup specification is satisfied in case of unreliability of certain input variables. We formally define the problem and characterize its worst-case complexity as 2EXPTIME-complete, like standard LTLf synthesis. Then we devise three different solution techniques: one based on direct automata manipulation, which is 2EXPTIME, one disregarding unreliable input variables by adopting a belief construction, which is 3EXPTIME, and one leveraging second-order quantified LTLf (QLTLf), which is 2EXPTIME and allows for a direct encoding into monadic second-order logic, which in turn is worst-case nonelementary. We prove their correctness and evaluate them against each other empirically. Interestingly, theoretical worst-case bounds do not translate into observed performance; the MSO technique performs best, followed by belief construction and direct automata manipulation. As a byproduct of our study, we provide a general synthesis procedure for arbitrary QLTLf specifications.

LTLf+ and PPLTL+: Extending LTLf and PPLTL to Infinite Traces

We introduce LTLf+ and PPLTL+, two logics to express properties of infinite traces, that are based on the linear-time temporal logics LTLf and PPLTL on finite traces. LTLf+/PPLTL+ use levels of Manna and Pnueli's LTL safety-progress hierarchy, and thus have the same expressive power as LTL. However, they also retain a crucial characteristic of the reactive synthesis problem for the base logics: the game arena for strategy extraction can be derived from deterministic finite automata (DFA). Consequently, these logics circumvent the notorious difficulties associated with determinizing infinite trace automata, typical of LTL reactive synthesis. We present DFA-based synthesis techniques for LTLf+/PPLTL+, and show that synthesis is 2EXPTIME-complete for LTLf+ (matching LTLf) and EXPTIME-complete for PPLTL+ (matching PPLTL). Notably, while PPLTL+ retains the full expressive power of LTL, reactive synthesis is EXPTIME-complete instead of 2EXPTIME-complete. The techniques are also adapted to optimally solve satisfiability, validity, and model-checking, to get EXPSPACE-complete for LTLf+ (extending a recent result for the guarantee level using LTLf), and PSPACE-complete for PPLTL+.

Encoding Reusable Multi-Robot Planning Strategies as Abstract Hypergraphs

Multi-Robot Task Planning (MR-TP) is the search for a discrete-action plan a team of robots should take to complete a task. The complexity of such problems scales exponentially with the number of robots and task complexity, making them challenging for online solution. To accelerate MR-TP over a system's lifetime, this work looks at combining two recent advances: (i) Decomposable State Space Hypergraph (DaSH), a novel hypergraph-based framework to efficiently model and solve MR-TP problems; and \mbox{(ii) learning-by-abstraction,} a technique that enables automatic extraction of generalizable planning strategies from individual planning experiences for later reuse. Specifically, we wish to extend this strategy-learning technique, originally designed for single-robot planning, to benefit multi-robot planning using hypergraph-based MR-TP.

On-the-fly Synthesis for LTL over Finite Traces: An Efficient Approach that Counts

We present an on-the-fly synthesis framework for Linear Temporal Logic over finite traces (LTLf) based on top-down deterministic automata construction. Existing approaches rely on constructing a complete Deterministic Finite Automaton (DFA) corresponding to the LTLf specification, a process with doubly exponential complexity relative to the formula size in the worst case. In this case, the synthesis procedure cannot be conducted until the entire DFA is constructed. This inefficiency is the main bottleneck of existing approaches. To address this challenge, we first present a method for converting LTLf into Transition-based DFA (TDFA) by directly leveraging LTLf semantics, incorporating intermediate results as direct components of the final automaton to enable parallelized synthesis and automata construction. We then explore the relationship between LTLf synthesis and TDFA games and subsequently develop an algorithm for performing LTLf synthesis using on-the-fly TDFA game solving. This algorithm traverses the state space in a global forward manner combined with a local backward method, along with the detection of strongly connected components. Moreover, we introduce two optimization techniques -- model-guided synthesis and state entailment -- to enhance the practical efficiency of our approach. Experimental results demonstrate that our on-the-fly approach achieves the best performance on the tested benchmarks and effectively complements existing tools and approaches.

Stochastic Games for Interactive Manipulation Domains

As robots become more prevalent, the complexity of robot-robot, robot-human, and robot-environment interactions increases. In these interactions, a robot needs to consider not only the effects of its own actions, but also the effects of other agents' actions and the possible interactions between agents. Previous works have considered reactive synthesis, where the human/environment is modeled as a deterministic, adversarial agent; as well as probabilistic synthesis, where the human/environment is modeled via a Markov chain. While they provide strong theoretical frameworks, there are still many aspects of human-robot interaction that cannot be fully expressed and many assumptions that must be made in each model. In this work, we propose stochastic games as a general model for human-robot interaction, which subsumes the expressivity of all previous representations. In addition, it allows us to make fewer modeling assumptions and leads to more natural and powerful models of interaction. We introduce the semantics of this abstraction and show how existing tools can be utilized to synthesize strategies to achieve complex tasks with guarantees. Further, we discuss the current computational limitations and improve the scalability by two orders of magnitude by a new way of constructing models for PRISM-games.

On Strategies in Synthesis Over Finite Traces

The innovations in reactive synthesis from {\em Linear Temporal Logics over finite traces} (LTLf) will be amplified by the ability to verify the correctness of the strategies generated by LTLf synthesis tools. This motivates our work on {\em LTLf model checking}. LTLf model checking, however, is not straightforward. The strategies generated by LTLf synthesis may be represented using {\em terminating} transducers or {\em non-terminating} transducers where executions are of finite-but-unbounded length or infinite length, respectively. For synthesis, there is no evidence that one type of transducer is better than the other since they both demonstrate the same complexity and similar algorithms. In this work, we show that for model checking, the two types of transducers are fundamentally different. Our central result is that LTLf model checking of non-terminating transducers is \emph{exponentially harder} than that of terminating transducers. We show that the problems are EXPSPACE-complete and PSPACE-complete, respectively. Hence, considering the feasibility of verification, LTLf synthesis tools should synthesize terminating transducers. This is, to the best of our knowledge, the \emph{first} evidence to use one transducer over the other in LTLf synthesis.

Solving Quantum-Inspired Perfect Matching Problems via Tutte's Theorem-Based Hybrid Boolean Constraints

Determining the satisfiability of Boolean constraint-satisfaction problems with different types of constraints, that is hybrid constraints, is a well-studied problem with important applications. We study here a new application of hybrid Boolean constraints, which arises in quantum computing. The problem relates to constrained perfect matching in edge-colored graphs. While general-purpose hybrid constraint solvers can be powerful, we show that direct encodings of the constrained-matching problem as hybrid constraints scale poorly and special techniques are still needed. We propose a novel encoding based on Tutte's Theorem in graph theory as well as optimization techniques. Empirical results demonstrate that our encoding, in suitable languages with advanced SAT solvers, scales significantly better than a number of competing approaches on constrained-matching benchmarks. Our study identifies the necessity of designing problem-specific encodings when applying powerful general-purpose constraint solvers.

Synthesis from Satisficing and Temporal Goals

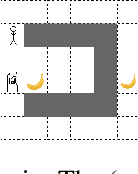
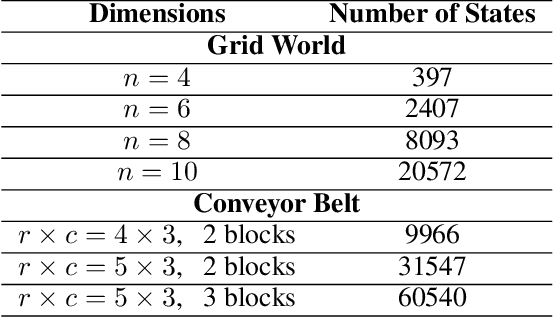
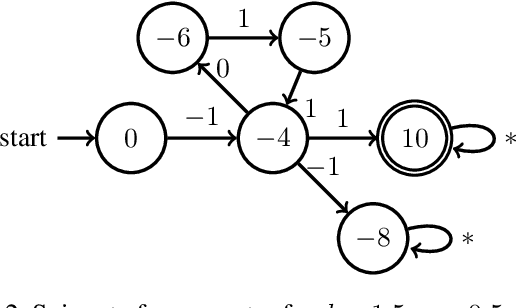
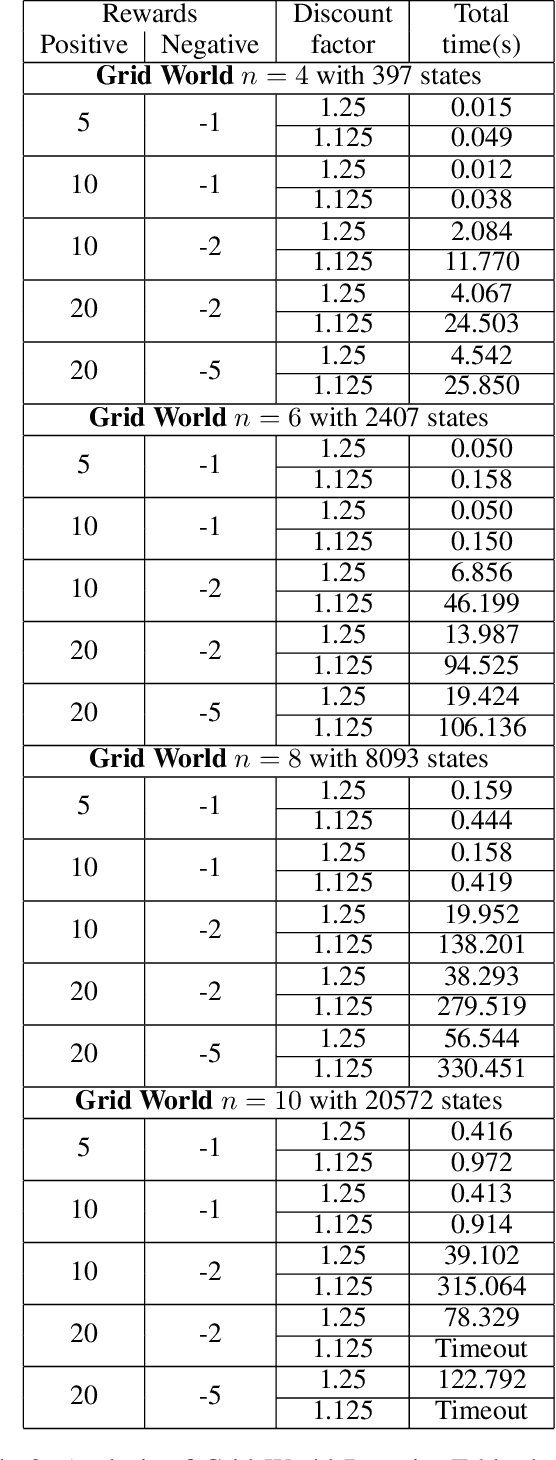
Reactive synthesis from high-level specifications that combine hard constraints expressed in Linear Temporal Logic LTL with soft constraints expressed by discounted-sum (DS) rewards has applications in planning and reinforcement learning. An existing approach combines techniques from LTL synthesis with optimization for the DS rewards but has failed to yield a sound algorithm. An alternative approach combining LTL synthesis with satisficing DS rewards (rewards that achieve a threshold) is sound and complete for integer discount factors, but, in practice, a fractional discount factor is desired. This work extends the existing satisficing approach, presenting the first sound algorithm for synthesis from LTL and DS rewards with fractional discount factors. The utility of our algorithm is demonstrated on robotic planning domains.

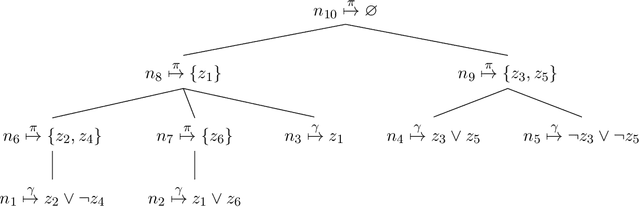
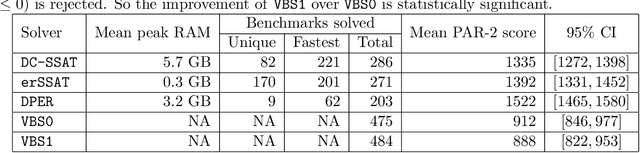
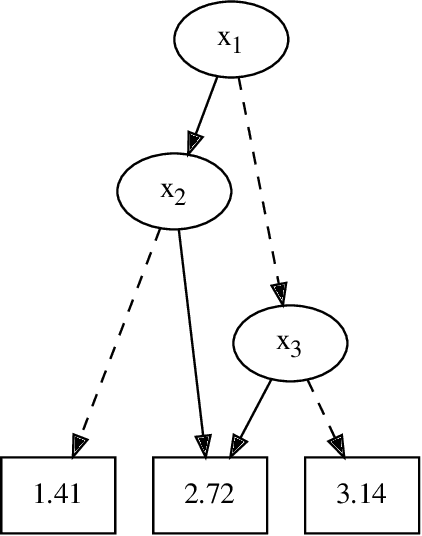
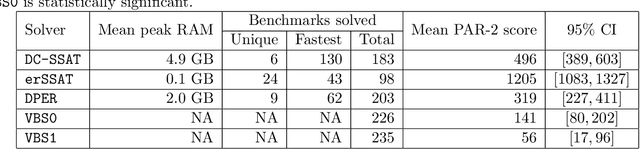
DPER: Dynamic Programming for Exist-Random Stochastic SAT

In Bayesian inference, the maximum a posteriori (MAP) problem combines the most probable explanation (MPE) and marginalization (MAR) problems. The counterpart in propositional logic is the exist-random stochastic satisfiability (ER-SSAT) problem, which combines the satisfiability (SAT) and weighted model counting (WMC) problems. Both MAP and ER-SSAT have the form $\operatorname{argmax}_X \sum_Y f(X, Y)$, where $f$ is a real-valued function over disjoint sets $X$ and $Y$ of variables. These two optimization problems request a value assignment for the $X$ variables that maximizes the weighted sum of $f(X, Y)$ over all value assignments for the $Y$ variables. ER-SSAT has been shown to be a promising approach to formally verify fairness in supervised learning. Recently, dynamic programming on graded project-join trees has been proposed to solve weighted projected model counting (WPMC), a related problem that has the form $\sum_X \max_Y f(X, Y)$. We extend this WPMC framework to exactly solve ER-SSAT and implement a dynamic-programming solver named DPER. Our empirical evaluation indicates that DPER contributes to the portfolio of state-of-the-art ER-SSAT solvers (DC-SSAT and erSSAT) through competitive performance on low-width problem instances.