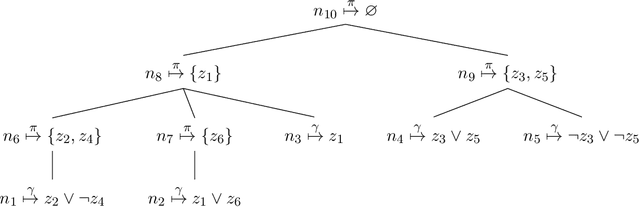
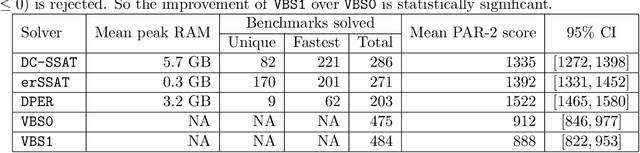
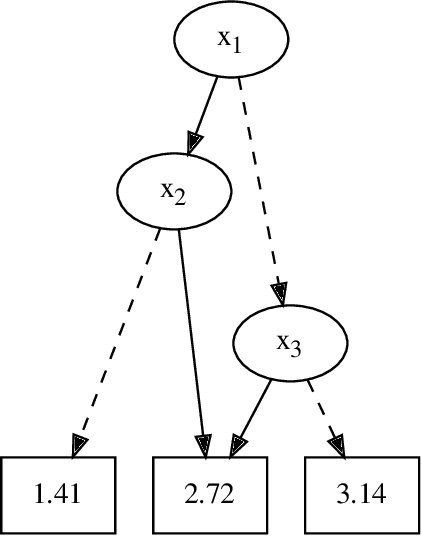
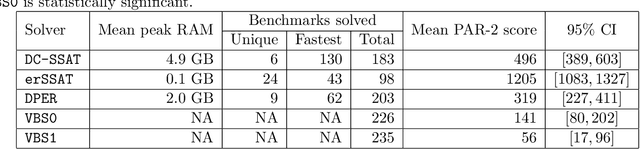
DPER: Dynamic Programming for Exist-Random Stochastic SAT

In Bayesian inference, the maximum a posteriori (MAP) problem combines the most probable explanation (MPE) and marginalization (MAR) problems. The counterpart in propositional logic is the exist-random stochastic satisfiability (ER-SSAT) problem, which combines the satisfiability (SAT) and weighted model counting (WMC) problems. Both MAP and ER-SSAT have the form $\operatorname{argmax}_X \sum_Y f(X, Y)$, where $f$ is a real-valued function over disjoint sets $X$ and $Y$ of variables. These two optimization problems request a value assignment for the $X$ variables that maximizes the weighted sum of $f(X, Y)$ over all value assignments for the $Y$ variables. ER-SSAT has been shown to be a promising approach to formally verify fairness in supervised learning. Recently, dynamic programming on graded project-join trees has been proposed to solve weighted projected model counting (WPMC), a related problem that has the form $\sum_X \max_Y f(X, Y)$. We extend this WPMC framework to exactly solve ER-SSAT and implement a dynamic-programming solver named DPER. Our empirical evaluation indicates that DPER contributes to the portfolio of state-of-the-art ER-SSAT solvers (DC-SSAT and erSSAT) through competitive performance on low-width problem instances.

DPO: Dynamic-Programming Optimization on Hybrid Constraints

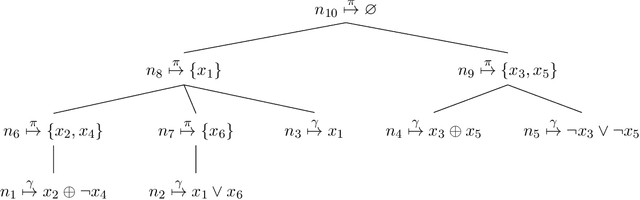
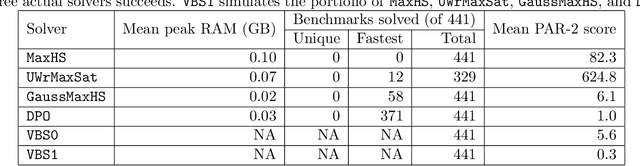
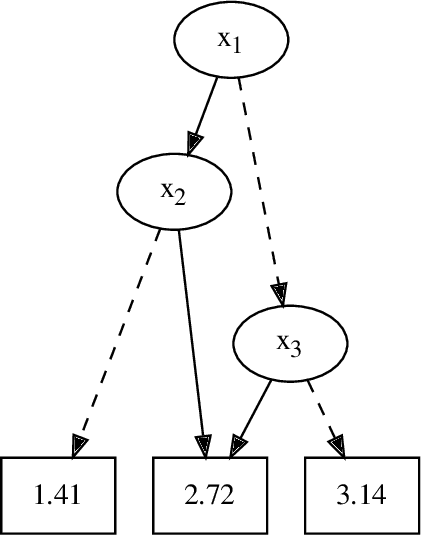
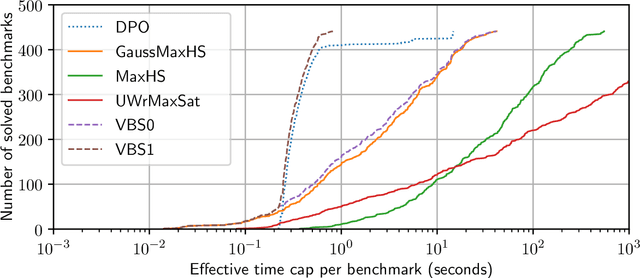
In Bayesian inference, the most probable explanation (MPE) problem requests a variable instantiation with the highest probability given some evidence. Since a Bayesian network can be encoded as a literal-weighted CNF formula $\varphi$, we study Boolean MPE, a more general problem that requests a model $\tau$ of $\varphi$ with the highest weight, where the weight of $\tau$ is the product of weights of literals satisfied by $\tau$. It is known that Boolean MPE can be solved via reduction to (weighted partial) MaxSAT. Recent work proposed DPMC, a dynamic-programming model counter that leverages graph-decomposition techniques to construct project-join trees. A project-join tree is an execution plan that specifies how to conjoin clauses and project out variables. We build on DPMC and introduce DPO, a dynamic-programming optimizer that exactly solves Boolean MPE. By using algebraic decision diagrams (ADDs) to represent pseudo-Boolean (PB) functions, DPO is able to handle disjunctive clauses as well as XOR clauses. (Cardinality constraints and PB constraints may also be compactly represented by ADDs, so one can further extend DPO's support for hybrid inputs.) To test the competitiveness of DPO, we generate random XOR-CNF formulas. On these hybrid benchmarks, DPO significantly outperforms MaxHS, UWrMaxSat, and GaussMaxHS, which are state-of-the-art exact solvers for MaxSAT.

DPMC: Weighted Model Counting by Dynamic Programming on Project-Join Trees

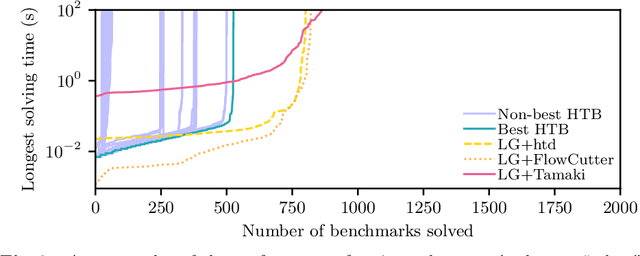
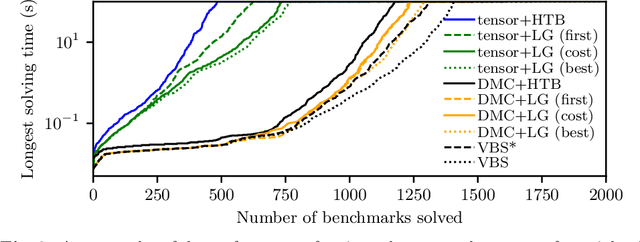
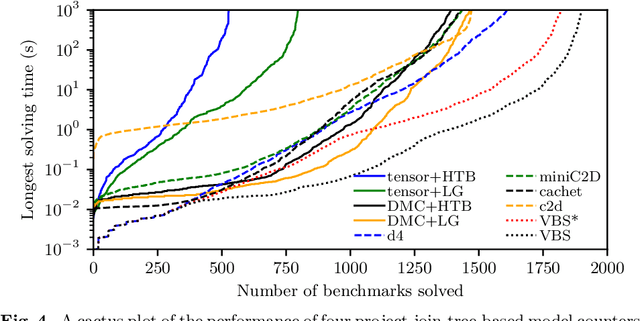
We propose a unifying dynamic-programming framework to compute exact literal-weighted model counts of formulas in conjunctive normal form. At the center of our framework are project-join trees, which specify efficient project-join orders to apply additive projections (variable eliminations) and joins (clause multiplications). In this framework, model counting is performed in two phases. First, the planning phase constructs a project-join tree from a formula. Second, the execution phase computes the model count of the formula, employing dynamic programming as guided by the project-join tree. We empirically evaluate various methods for the planning phase and compare constraint-satisfaction heuristics with tree-decomposition tools. We also investigate the performance of different data structures for the execution phase and compare algebraic decision diagrams with tensors. We show that our dynamic-programming model-counting framework DPMC is competitive with the state-of-the-art exact weighted model counters cachet, c2d, d4, and miniC2D.

ADDMC: Exact Weighted Model Counting with Algebraic Decision Diagrams

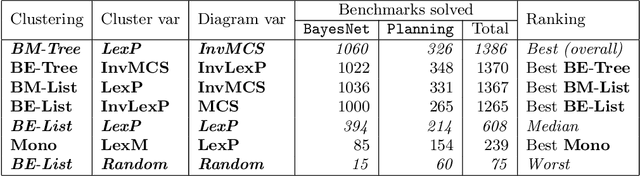
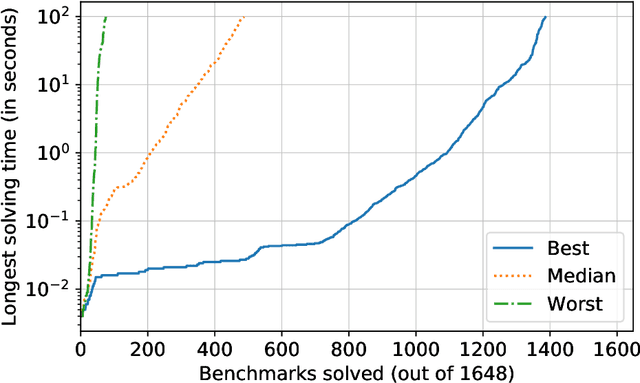
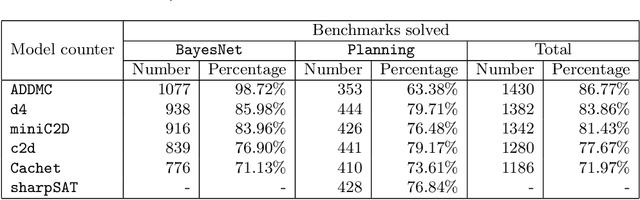
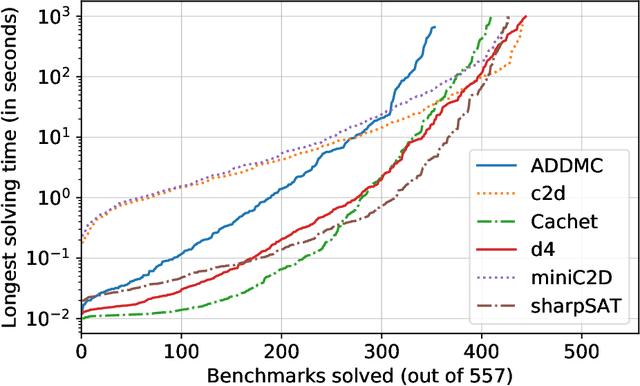
We compute exact literal-weighted model counts of CNF formulas. Our algorithm employs dynamic programming, with Algebraic Decision Diagrams as the primary data structure. This technique is implemented in ADDMC, a new model counter. We empirically evaluate various heuristics that can be used with ADDMC. We also compare ADDMC to state-of-the-art exact model counters (Cachet, c2d, d4, miniC2D, and sharpSAT) on the two largest CNF model counting benchmark families (BayesNet and Planning). ADDMC solves the most benchmarks in total within the given timeout.