LTLf Synthesis Under Environment Specifications for Reachability and Safety Properties

In this paper, we study LTLf synthesis under environment specifications for arbitrary reachability and safety properties. We consider both kinds of properties for both agent tasks and environment specifications, providing a complete landscape of synthesis algorithms. For each case, we devise a specific algorithm (optimal wrt complexity of the problem) and prove its correctness. The algorithms combine common building blocks in different ways. While some cases are already studied in literature others are studied here for the first time.

Sufficient reasons for classifier decisions in the presence of constraints

Recent work has unveiled a theory for reasoning about the decisions made by binary classifiers: a classifier describes a Boolean function, and the reasons behind an instance being classified as positive are the prime-implicants of the function that are satisfied by the instance. One drawback of these works is that they do not explicitly treat scenarios where the underlying data is known to be constrained, e.g., certain combinations of features may not exist, may not be observable, or may be required to be disregarded. We propose a more general theory, also based on prime-implicants, tailored to taking constraints into account. The main idea is to view classifiers in the presence of constraints as describing partial Boolean functions, i.e., that are undefined on instances that do not satisfy the constraints. We prove that this simple idea results in reasons that are no less (and sometimes more) succinct. That is, not taking constraints into account (e.g., ignored, or taken as negative instances) results in reasons that are subsumed by reasons that do take constraints into account. We illustrate this improved parsimony on synthetic classifiers and classifiers learned from real data.

Equilibria for Games with Combined Qualitative and Quantitative Objectives

The overall aim of our research is to develop techniques to reason about the equilibrium properties of multi-agent systems. We model multi-agent systems as concurrent games, in which each player is a process that is assumed to act independently and strategically in pursuit of personal preferences. In this article, we study these games in the context of finite-memory strategies, and we assume players' preferences are defined by a qualitative and a quantitative objective, which are related by a lexicographic order: a player first prefers to satisfy its qualitative objective (given as a formula of Linear Temporal Logic) and then prefers to minimise costs (given by a mean-payoff function). Our main result is that deciding the existence of a strict epsilon Nash equilibrium in such games is 2ExpTime-complete (and hence decidable), even if players' deviations are implemented as infinite-memory strategies.

Stochastic Fairness and Language-Theoretic Fairness in Planning on Nondeterministic Domains

We address two central notions of fairness in the literature of planning on nondeterministic fully observable domains. The first, which we call stochastic fairness, is classical, and assumes an environment which operates probabilistically using possibly unknown probabilities. The second, which is language-theoretic, assumes that if an action is taken from a given state infinitely often then all its possible outcomes should appear infinitely often (we call this state-action fairness). While the two notions coincide for standard reachability goals, they diverge for temporally extended goals. This important difference has been overlooked in the planning literature, and we argue has led to confusion in a number of published algorithms which use reductions that were stated for state-action fairness, for which they are incorrect, while being correct for stochastic fairness. We remedy this and provide an optimal sound and complete algorithm for solving state-action fair planning for LTL/LTLf goals, as well as a correct proof of the lower bound of the goal-complexity (our proof is general enough that it provides new proofs also for the no-fairness and stochastic-fairness cases). Overall, we show that stochastic fairness is better behaved than state-action fairness.

Generalized Planning: Non-Deterministic Abstractions and Trajectory Constraints

We study the characterization and computation of general policies for families of problems that share a structure characterized by a common reduction into a single abstract problem. Policies $\mu$ that solve the abstract problem P have been shown to solve all problems Q that reduce to P provided that $\mu$ terminates in Q. In this work, we shed light on why this termination condition is needed and how it can be removed. The key observation is that the abstract problem P captures the common structure among the concrete problems Q that is local (Markovian) but misses common structure that is global. We show how such global structure can be captured by means of trajectory constraints that in many cases can be expressed as LTL formulas, thus reducing generalized planning to LTL synthesis. Moreover, for a broad class of problems that involve integer variables that can be increased or decreased, trajectory constraints can be compiled away, reducing generalized planning to fully observable non-deterministic planning.

Changing Observations in Epistemic Temporal Logic

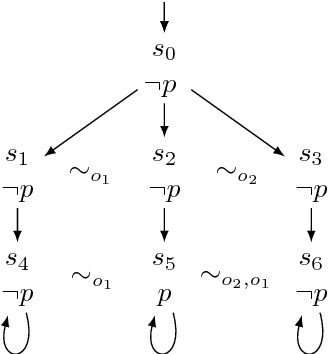
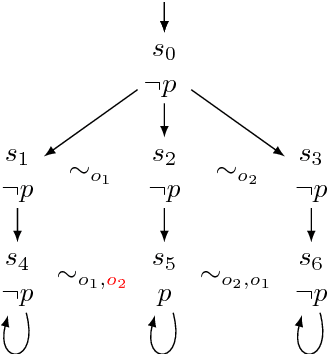
We study dynamic changes of agents' observational power in logics of knowledge and time. We consider CTL*K, the extension of CTL* with knowledge operators, and enrich it with a new operator that models a change in an agent's way of observing the system. We extend the classic semantics of knowledge for perfect-recall agents to account for changes of observation, and we show that this new operator strictly increases the expressivity of CTL*K. We reduce the model-checking problem for our logic to that for CTL*K, which is known to be decidable. This provides a solution to the model-checking problem for our logic, but its complexity is not optimal. Indeed we provide a direct decision procedure with better complexity.

Planning and Synthesis Under Assumptions

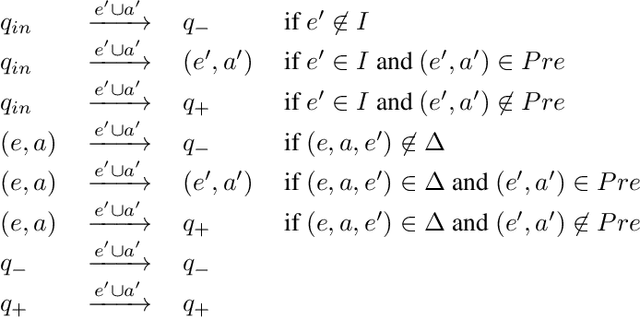
In Reasoning about Action and Planning, one synthesizes the agent plan by taking advantage of the assumption on how the environment works (that is, one exploits the environment's effects, its fairness, its trajectory constraints). In this paper we study this form of synthesis in detail. We consider assumptions as constraints on the possible strategies that the environment can have in order to respond to the agent's actions. Such constraints may be given in the form of a planning domain (or action theory), as linear-time formulas over infinite or finite runs, or as a combination of the two (e.g., FOND under fairness). We argue though that not all assumption specifications are meaningful: they need to be consistent, which means that there must exist an environment strategy fulfilling the assumption in spite of the agent actions. For such assumptions, we study how to do synthesis/planning for agent goals, ranging from a classical reachability to goal on traces specified in LTL and LTLf/LDLf, characterizing the problem both mathematically and algorithmically.

Extended Graded Modalities in Strategy Logic

Strategy Logic (SL) is a logical formalism for strategic reasoning in multi-agent systems. Its main feature is that it has variables for strategies that are associated to specific agents with a binding operator. We introduce Graded Strategy Logic (GradedSL), an extension of SL by graded quantifiers over tuples of strategy variables, i.e., "there exist at least g different tuples (x_1,...,x_n) of strategies" where g is a cardinal from the set N union {aleph_0, aleph_1, 2^aleph_0}. We prove that the model-checking problem of GradedSL is decidable. We then turn to the complexity of fragments of GradedSL. When the g's are restricted to finite cardinals, written GradedNSL, the complexity of model-checking is no harder than for SL, i.e., it is non-elementary in the quantifier rank. We illustrate our formalism by showing how to count the number of different strategy profiles that are Nash equilibria (NE), or subgame-perfect equilibria (SPE). By analyzing the structure of the specific formulas involved, we conclude that the important problems of checking for the existence of a unique NE or SPE can both be solved in 2ExpTime, which is not harder than merely checking for the existence of such equilibria.