Consistent Submodular Maximization

Maximizing monotone submodular functions under cardinality constraints is a classic optimization task with several applications in data mining and machine learning. In this paper we study this problem in a dynamic environment with consistency constraints: elements arrive in a streaming fashion and the goal is maintaining a constant approximation to the optimal solution while having a stable solution (i.e., the number of changes between two consecutive solutions is bounded). We provide algorithms in this setting with different trade-offs between consistency and approximation quality. We also complement our theoretical results with an experimental analysis showing the effectiveness of our algorithms in real-world instances.

GIST: Greedy Independent Set Thresholding for Diverse Data Summarization

We propose a novel subset selection task called min-distance diverse data summarization ($\textsf{MDDS}$), which has a wide variety of applications in machine learning, e.g., data sampling and feature selection. Given a set of points in a metric space, the goal is to maximize an objective that combines the total utility of the points and a diversity term that captures the minimum distance between any pair of selected points, subject to the constraint $|S| \le k$. For example, the points may correspond to training examples in a data sampling problem, e.g., learned embeddings of images extracted from a deep neural network. This work presents the $\texttt{GIST}$ algorithm, which achieves a $\frac{2}{3}$-approximation guarantee for $\textsf{MDDS}$ by approximating a series of maximum independent set problems with a bicriteria greedy algorithm. We also prove a complementary $(\frac{2}{3}+\varepsilon)$-hardness of approximation, for any $\varepsilon > 0$. Finally, we provide an empirical study that demonstrates $\texttt{GIST}$ outperforms existing methods for $\textsf{MDDS}$ on synthetic data, and also for a real-world image classification experiment the studies single-shot subset selection for ImageNet.

Fully Dynamic Submodular Maximization over Matroids

Maximizing monotone submodular functions under a matroid constraint is a classic algorithmic problem with multiple applications in data mining and machine learning. We study this classic problem in the fully dynamic setting, where elements can be both inserted and deleted in real-time. Our main result is a randomized algorithm that maintains an efficient data structure with an $\tilde{O}(k^2)$ amortized update time (in the number of additions and deletions) and yields a $4$-approximate solution, where $k$ is the rank of the matroid.

Deletion Robust Non-Monotone Submodular Maximization over Matroids

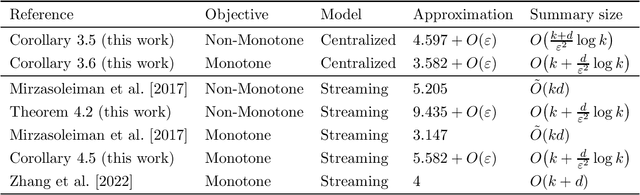
Maximizing a submodular function is a fundamental task in machine learning and in this paper we study the deletion robust version of the problem under the classic matroids constraint. Here the goal is to extract a small size summary of the dataset that contains a high value independent set even after an adversary deleted some elements. We present constant-factor approximation algorithms, whose space complexity depends on the rank $k$ of the matroid and the number $d$ of deleted elements. In the centralized setting we present a $(4.597+O(\varepsilon))$-approximation algorithm with summary size $O( \frac{k+d}{\varepsilon^2}\log \frac{k}{\varepsilon})$ that is improved to a $(3.582+O(\varepsilon))$-approximation with $O(k + \frac{d}{\varepsilon^2}\log \frac{k}{\varepsilon})$ summary size when the objective is monotone. In the streaming setting we provide a $(9.435 + O(\varepsilon))$-approximation algorithm with summary size and memory $O(k + \frac{d}{\varepsilon^2}\log \frac{k}{\varepsilon})$; the approximation factor is then improved to $(5.582+O(\varepsilon))$ in the monotone case.

Deletion Robust Submodular Maximization over Matroids

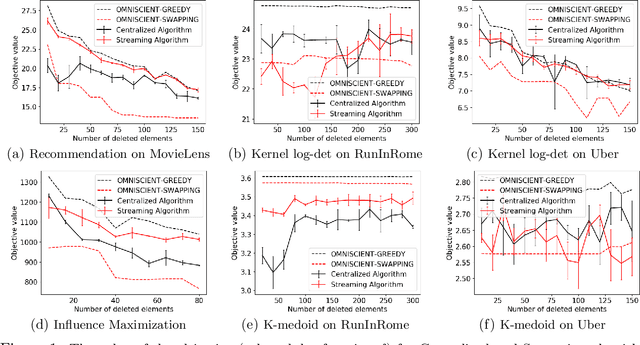
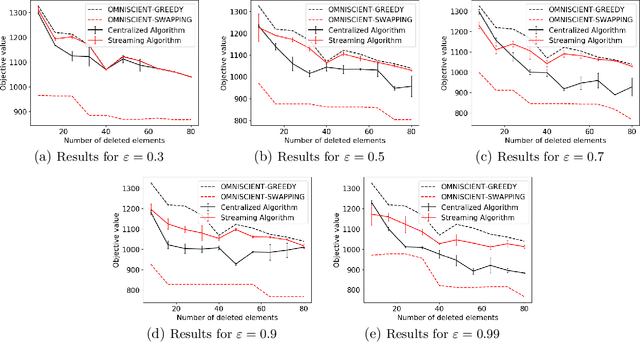
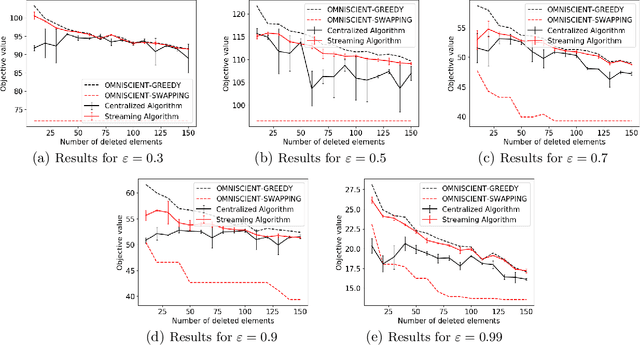
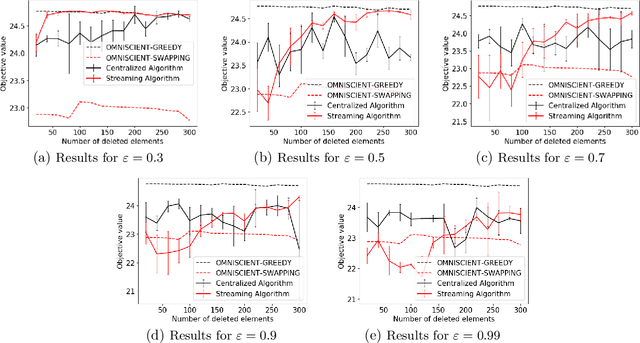
Maximizing a monotone submodular function is a fundamental task in machine learning. In this paper, we study the deletion robust version of the problem under the classic matroids constraint. Here the goal is to extract a small size summary of the dataset that contains a high value independent set even after an adversary deleted some elements. We present constant-factor approximation algorithms, whose space complexity depends on the rank $k$ of the matroid and the number $d$ of deleted elements. In the centralized setting we present a $(3.582+O(\varepsilon))$-approximation algorithm with summary size $O(k + \frac{d \log k}{\varepsilon^2})$. In the streaming setting we provide a $(5.582+O(\varepsilon))$-approximation algorithm with summary size and memory $O(k + \frac{d \log k}{\varepsilon^2})$. We complement our theoretical results with an in-depth experimental analysis showing the effectiveness of our algorithms on real-world datasets.

Submodular Streaming in All its Glory: Tight Approximation, Minimum Memory and Low Adaptive Complexity

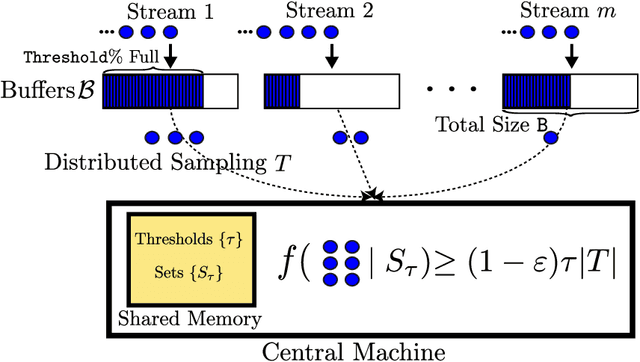
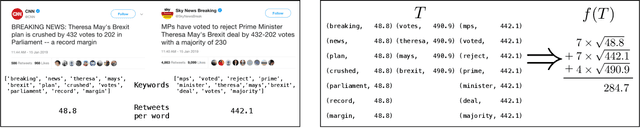
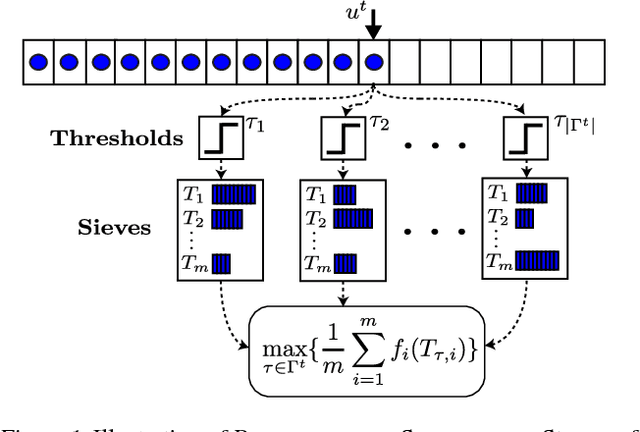
Streaming algorithms are generally judged by the quality of their solution, memory footprint, and computational complexity. In this paper, we study the problem of maximizing a monotone submodular function in the streaming setting with a cardinality constraint $k$. We first propose Sieve-Streaming++, which requires just one pass over the data, keeps only $O(k)$ elements and achieves the tight $(1/2)$-approximation guarantee. The best previously known streaming algorithms either achieve a suboptimal $(1/4)$-approximation with $\Theta(k)$ memory or the optimal $(1/2)$-approximation with $O(k\log k)$ memory. Next, we show that by buffering a small fraction of the stream and applying a careful filtering procedure, one can heavily reduce the number of adaptive computational rounds, thus substantially lowering the computational complexity of Sieve-Streaming++. We then generalize our results to the more challenging multi-source streaming setting. We show how one can achieve the tight $(1/2)$-approximation guarantee with $O(k)$ shared memory while minimizing not only the required rounds of computations but also the total number of communicated bits. Finally, we demonstrate the efficiency of our algorithms on real-world data summarization tasks for multi-source streams of tweets and of YouTube videos.

Data Summarization at Scale: A Two-Stage Submodular Approach

The sheer scale of modern datasets has resulted in a dire need for summarization techniques that identify representative elements in a dataset. Fortunately, the vast majority of data summarization tasks satisfy an intuitive diminishing returns condition known as submodularity, which allows us to find nearly-optimal solutions in linear time. We focus on a two-stage submodular framework where the goal is to use some given training functions to reduce the ground set so that optimizing new functions (drawn from the same distribution) over the reduced set provides almost as much value as optimizing them over the entire ground set. In this paper, we develop the first streaming and distributed solutions to this problem. In addition to providing strong theoretical guarantees, we demonstrate both the utility and efficiency of our algorithms on real-world tasks including image summarization and ride-share optimization.

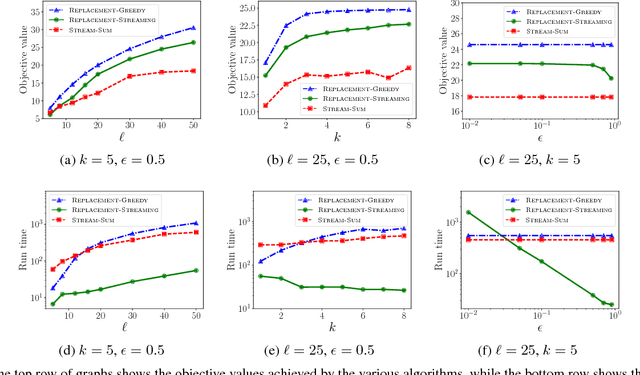
Deletion-Robust Submodular Maximization at Scale

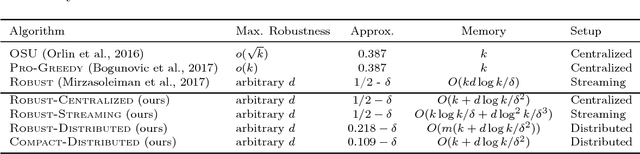
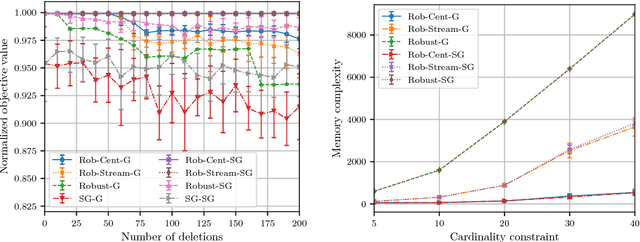
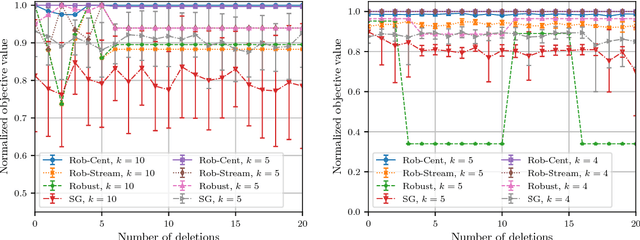
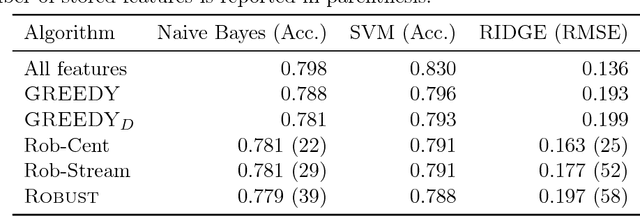
Can we efficiently extract useful information from a large user-generated dataset while protecting the privacy of the users and/or ensuring fairness in representation. We cast this problem as an instance of a deletion-robust submodular maximization where part of the data may be deleted due to privacy concerns or fairness criteria. We propose the first memory-efficient centralized, streaming, and distributed methods with constant-factor approximation guarantees against any number of adversarial deletions. We extensively evaluate the performance of our algorithms against prior state-of-the-art on real-world applications, including (i) Uber-pick up locations with location privacy constraints; (ii) feature selection with fairness constraints for income prediction and crime rate prediction; and (iii) robust to deletion summarization of census data, consisting of 2,458,285 feature vectors.

Horizontally Scalable Submodular Maximization

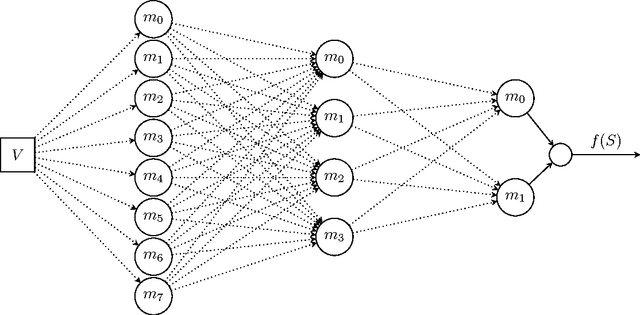
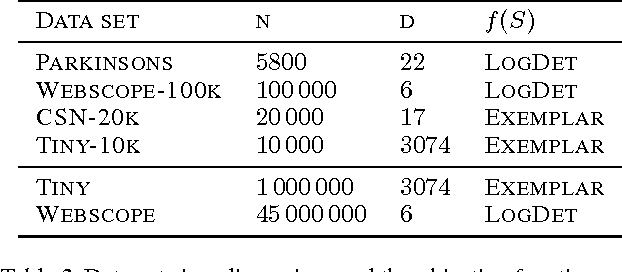
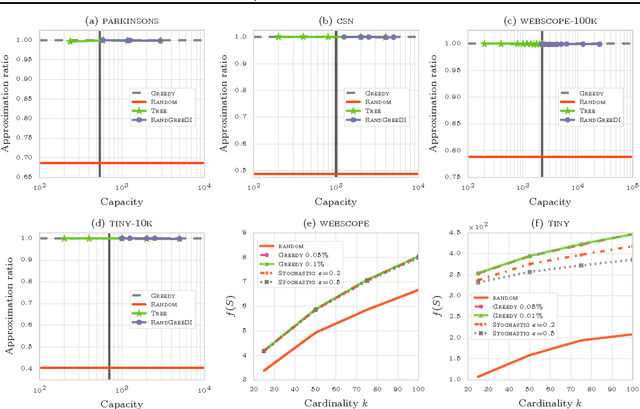
A variety of large-scale machine learning problems can be cast as instances of constrained submodular maximization. Existing approaches for distributed submodular maximization have a critical drawback: The capacity - number of instances that can fit in memory - must grow with the data set size. In practice, while one can provision many machines, the capacity of each machine is limited by physical constraints. We propose a truly scalable approach for distributed submodular maximization under fixed capacity. The proposed framework applies to a broad class of algorithms and constraints and provides theoretical guarantees on the approximation factor for any available capacity. We empirically evaluate the proposed algorithm on a variety of data sets and demonstrate that it achieves performance competitive with the centralized greedy solution.

Sparse Solutions to Nonnegative Linear Systems and Applications

We give an efficient algorithm for finding sparse approximate solutions to linear systems of equations with nonnegative coefficients. Unlike most known results for sparse recovery, we do not require {\em any} assumption on the matrix other than non-negativity. Our algorithm is combinatorial in nature, inspired by techniques for the set cover problem, as well as the multiplicative weight update method. We then present a natural application to learning mixture models in the PAC framework. For learning a mixture of $k$ axis-aligned Gaussians in $d$ dimensions, we give an algorithm that outputs a mixture of $O(k/\epsilon^3)$ Gaussians that is $\epsilon$-close in statistical distance to the true distribution, without any separation assumptions. The time and sample complexity is roughly $O(kd/\epsilon^3)^{d}$. This is polynomial when $d$ is constant -- precisely the regime in which known methods fail to identify the components efficiently. Given that non-negativity is a natural assumption, we believe that our result may find use in other settings in which we wish to approximately explain data using a small number of a (large) candidate set of components.