VILD: Variational Imitation Learning with Diverse-quality Demonstrations

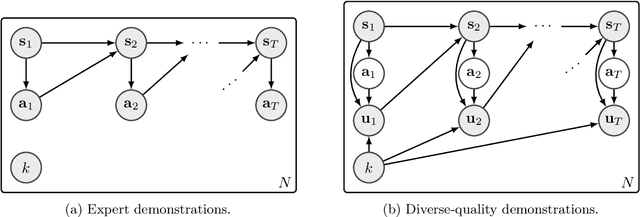
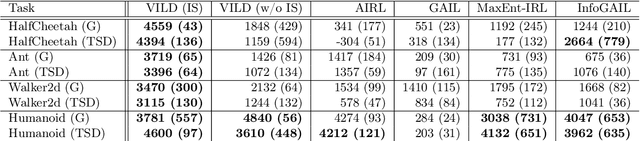
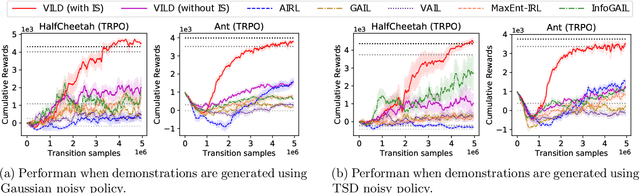
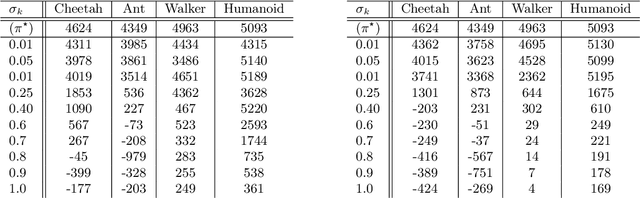
The goal of imitation learning (IL) is to learn a good policy from high-quality demonstrations. However, the quality of demonstrations in reality can be diverse, since it is easier and cheaper to collect demonstrations from a mix of experts and amateurs. IL in such situations can be challenging, especially when the level of demonstrators' expertise is unknown. We propose a new IL method called \underline{v}ariational \underline{i}mitation \underline{l}earning with \underline{d}iverse-quality demonstrations (VILD), where we explicitly model the level of demonstrators' expertise with a probabilistic graphical model and estimate it along with a reward function. We show that a naive approach to estimation is not suitable to large state and action spaces, and fix its issues by using a variational approach which can be easily implemented using existing reinforcement learning methods. Experiments on continuous-control benchmarks demonstrate that VILD outperforms state-of-the-art methods. Our work enables scalable and data-efficient IL under more realistic settings than before.

Fast and Simple Natural-Gradient Variational Inference with Mixture of Exponential-family Approximations

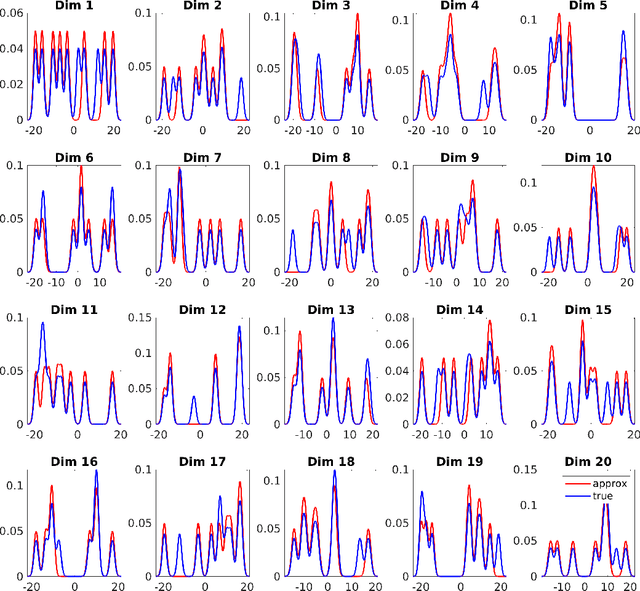
Natural-gradient methods enable fast and simple algorithms for variational inference, but due to computational difficulties, their use is mostly limited to \emph{minimal} exponential-family (EF) approximations. In this paper, we extend their application to estimate \emph{structured} approximations such as mixtures of EF distributions. Such approximations can fit complex, multimodal posterior distributions and are generally more accurate than unimodal EF approximations. By using a \emph{minimal conditional-EF} representation of such approximations, we derive simple natural-gradient updates. Our empirical results demonstrate a faster convergence of our natural-gradient method compared to black-box gradient-based methods. Our work expands the scope of natural gradients for Bayesian inference and makes them more widely applicable than before.

Practical Deep Learning with Bayesian Principles

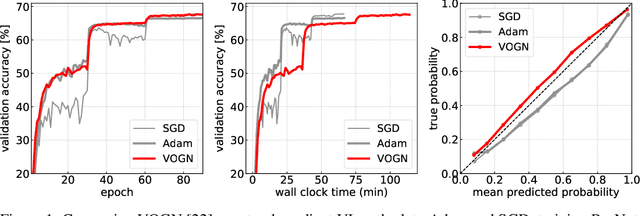
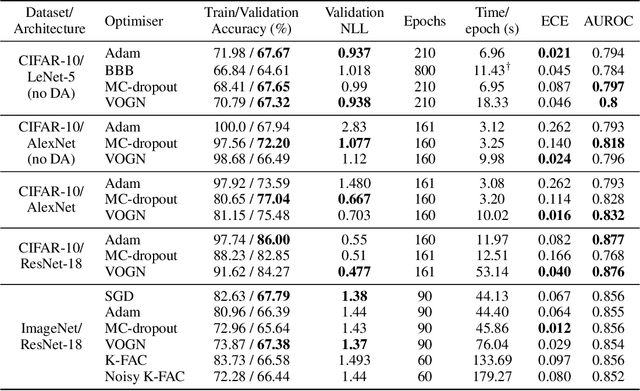
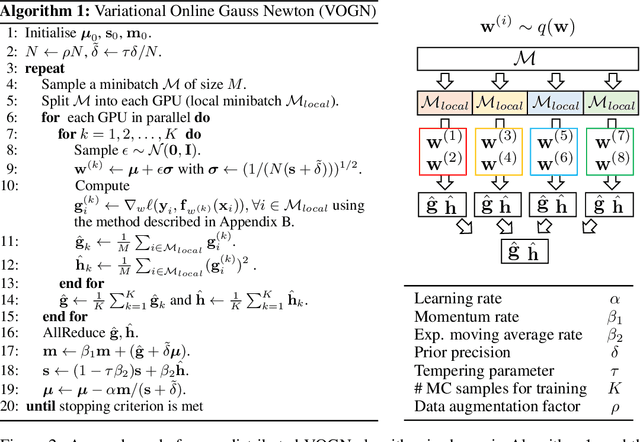
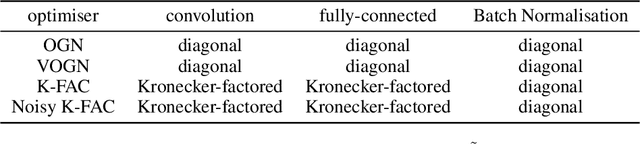
Bayesian methods promise to fix many shortcomings of deep learning, but they are impractical and rarely match the performance of standard methods, let alone improve them. In this paper, we demonstrate practical training of deep networks with natural-gradient variational inference. By applying techniques such as batch normalisation, data augmentation, and distributed training, we achieve similar performance in about the same number of epochs as the Adam optimiser, even on large datasets such as ImageNet. Importantly, the benefits of Bayesian principles are preserved: predictive probabilities are well-calibrated and uncertainties on out-of-distribution data are improved. This work enables practical deep learning while preserving benefits of Bayesian principles. A PyTorch implementation will be available as a plug-and-play optimiser.

Approximate Inference Turns Deep Networks into Gaussian Processes

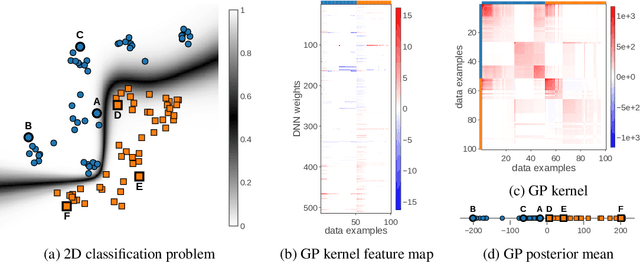
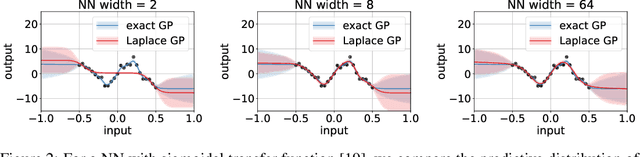
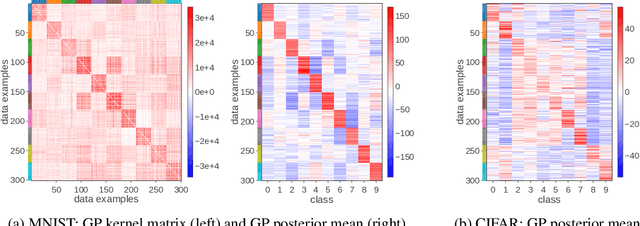
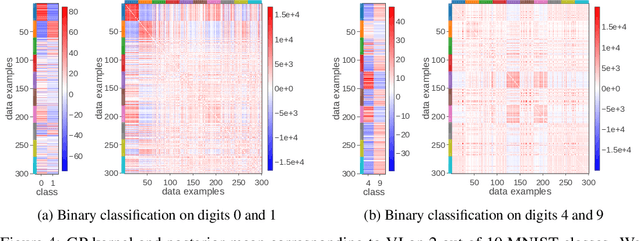
Deep neural networks (DNN) and Gaussian processes (GP) are two powerful models with several theoretical connections relating them, but the relationship between their training methods is not well understood. In this paper, we show that certain Gaussian posterior approximations for Bayesian DNNs are equivalent to GP posteriors. As a result, we can obtain a GP kernel and a nonlinear feature map simply by training the DNN. Surprisingly, the resulting kernel is the neural tangent kernel which has desirable theoretical properties for infinitely-wide DNNs. We show feature maps obtained on real datasets and demonstrate the use of the GP marginal likelihood to tune hyperparameters of DNNs. Our work aims to facilitate further research on combining DNNs and GPs in practical settings.

Scalable Training of Inference Networks for Gaussian-Process Models

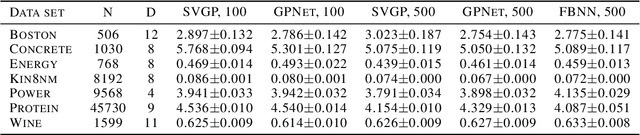
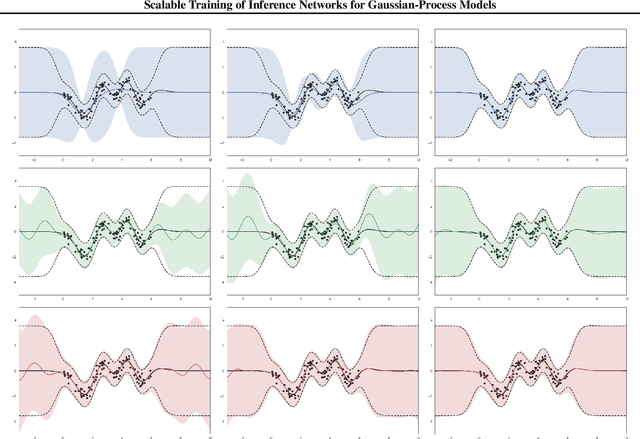
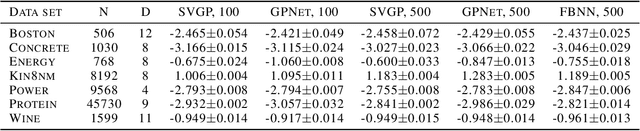
Inference in Gaussian process (GP) models is computationally challenging for large data, and often difficult to approximate with a small number of inducing points. We explore an alternative approximation that employs stochastic inference networks for a flexible inference. Unfortunately, for such networks, minibatch training is difficult to be able to learn meaningful correlations over function outputs for a large dataset. We propose an algorithm that enables such training by tracking a stochastic, functional mirror-descent algorithm. At each iteration, this only requires considering a finite number of input locations, resulting in a scalable and easy-to-implement algorithm. Empirical results show comparable and, sometimes, superior performance to existing sparse variational GP methods.

A Generalization Bound for Online Variational Inference

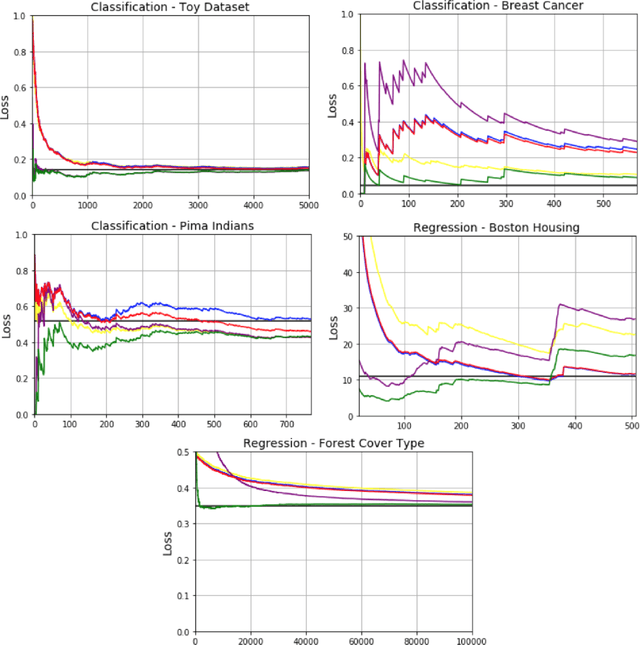
Bayesian inference provides an attractive online-learning framework to analyze sequential data, and offers generalization guarantees which hold even under model mismatch and with adversaries. Unfortunately, exact Bayesian inference is rarely feasible in practice and approximation methods are usually employed, but do such methods preserve the generalization properties of Bayesian inference? In this paper, we show that this is indeed the case for some variational inference (VI) algorithms. We propose new online, tempered VI algorithms and derive their generalization bounds. Our theoretical result relies on the convexity of the variational objective, but we argue that our result should hold more generally and present empirical evidence in support of this. Our work in this paper presents theoretical justifications in favor of online algorithms that rely on approximate Bayesian methods.

TD-Regularized Actor-Critic Methods

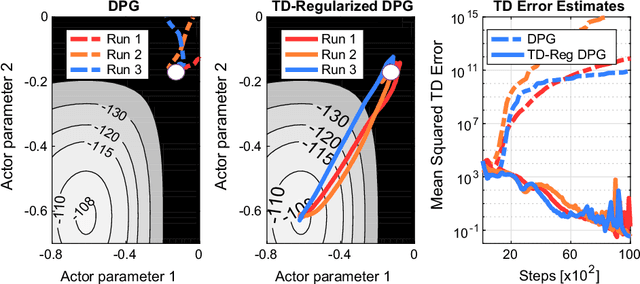
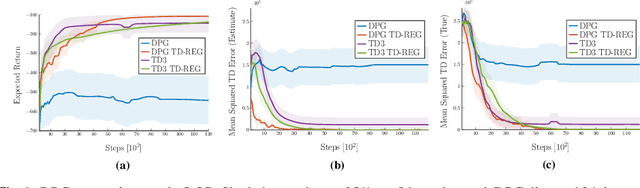
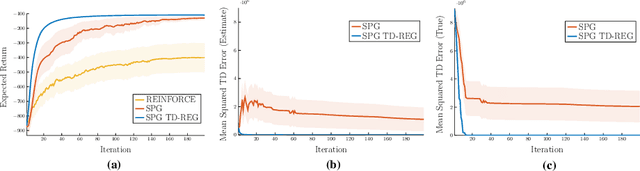
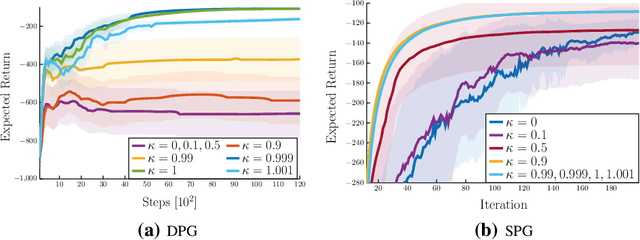
Actor-critic methods can achieve incredible performance on difficult reinforcement learning problems, but they are also prone to instability. This is partly due to the interaction between the actor and critic during learning, e.g., an inaccurate step taken by one of them might adversely affect the other and destabilize the learning. To avoid such issues, we propose to regularize the learning objective of the actor by penalizing the temporal difference (TD) error of the critic. This improves stability by avoiding large steps in the actor update whenever the critic is highly inaccurate. The resulting method, which we call the TD-regularized actor-critic method, is a simple plug-and-play approach to improve stability and overall performance of the actor-critic methods. Evaluations on standard benchmarks confirm this.

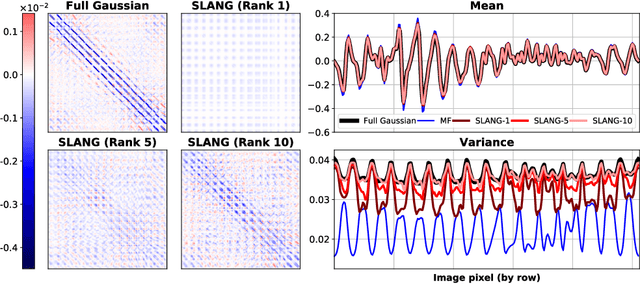
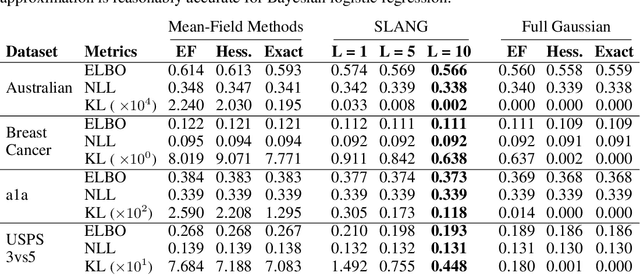
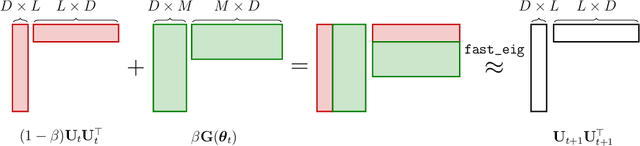
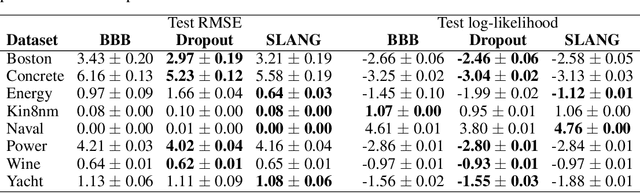
SLANG: Fast Structured Covariance Approximations for Bayesian Deep Learning with Natural Gradient

Uncertainty estimation in large deep-learning models is a computationally challenging task, where it is difficult to form even a Gaussian approximation to the posterior distribution. In such situations, existing methods usually resort to a diagonal approximation of the covariance matrix despite, the fact that these matrices are known to give poor uncertainty estimates. To address this issue, we propose a new stochastic, low-rank, approximate natural-gradient (SLANG) method for variational inference in large, deep models. Our method estimates a "diagonal plus low-rank" structure based solely on back-propagated gradients of the network log-likelihood. This requires strictly less gradient computations than methods that compute the gradient of the whole variational objective. Empirical evaluations on standard benchmarks confirm that SLANG enables faster and more accurate estimation of uncertainty than mean-field methods, and performs comparably to state-of-the-art methods.

Exact Recovery of Low-rank Tensor Decomposition under Reshuffling

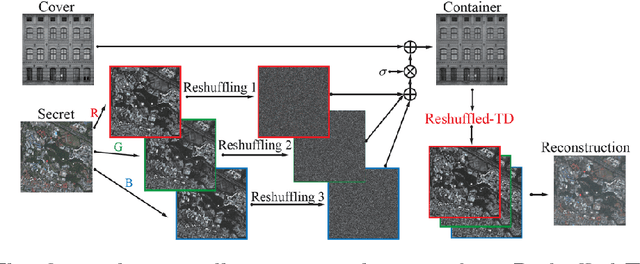
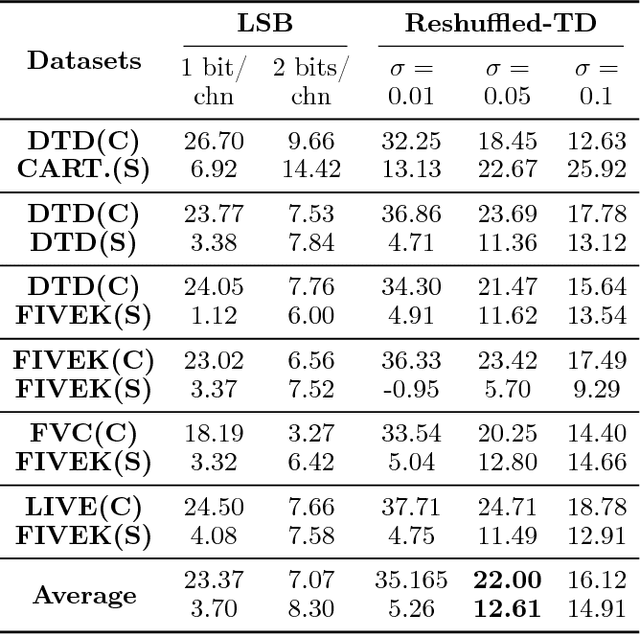
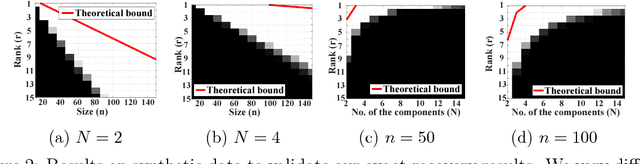
Low-rank tensor decomposition is a promising approach for analysis and understanding of real-world data. Many such analyses require correct recovery of the true latent factors, but the conditions of exact recovery are not known for many existing tensor decomposition methods. In this paper, we derive such conditions for a general class of tensor decomposition methods where each latent tensor component can be reshuffled into a low-rank matrix of arbitrary shape. The reshuffling operation generalizes the traditional unfolding operation, and provides flexibility to recover true latent factors of complex data-structures. We prove that exact recovery can be guaranteed by using a convex program when a type of incoherence measure is upper bounded. The results on image steganography show that our method obtains the state-of-the-art performance. The theoretical analysis in this paper is expected to be useful to derive similar results for other types of tensor-decomposition methods.

Fast and Scalable Bayesian Deep Learning by Weight-Perturbation in Adam

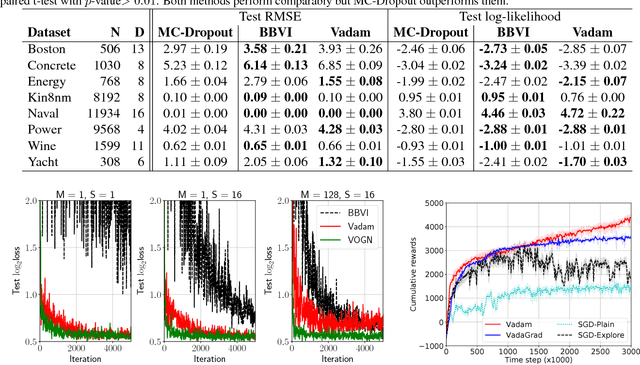
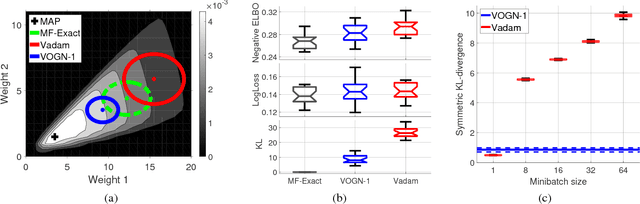
Uncertainty computation in deep learning is essential to design robust and reliable systems. Variational inference (VI) is a promising approach for such computation, but requires more effort to implement and execute compared to maximum-likelihood methods. In this paper, we propose new natural-gradient algorithms to reduce such efforts for Gaussian mean-field VI. Our algorithms can be implemented within the Adam optimizer by perturbing the network weights during gradient evaluations, and uncertainty estimates can be cheaply obtained by using the vector that adapts the learning rate. This requires lower memory, computation, and implementation effort than existing VI methods, while obtaining uncertainty estimates of comparable quality. Our empirical results confirm this and further suggest that the weight-perturbation in our algorithm could be useful for exploration in reinforcement learning and stochastic optimization.