Exact Recovery of Low-rank Tensor Decomposition under Reshuffling

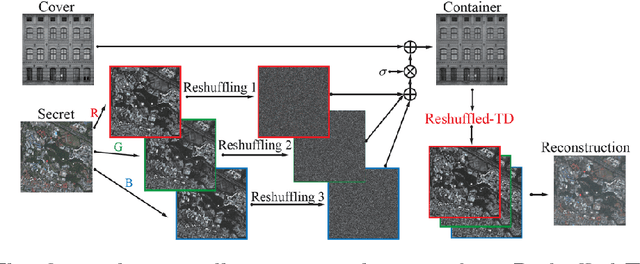
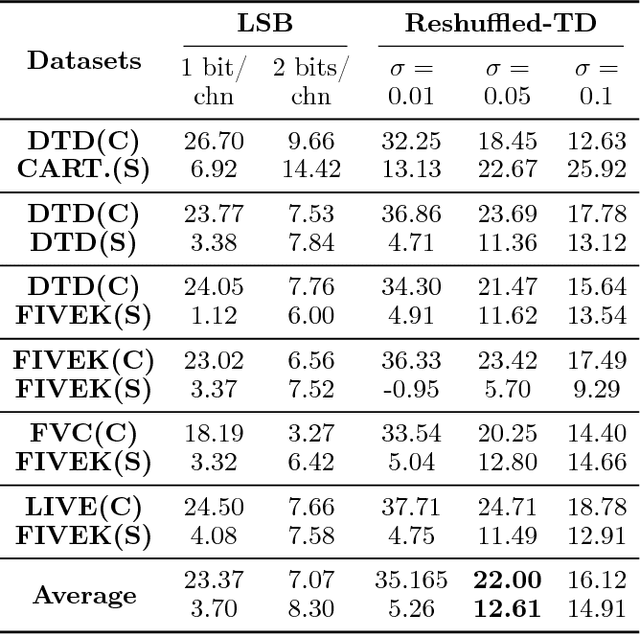
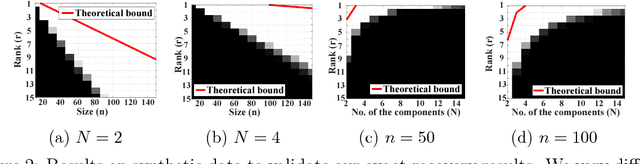
Low-rank tensor decomposition is a promising approach for analysis and understanding of real-world data. Many such analyses require correct recovery of the true latent factors, but the conditions of exact recovery are not known for many existing tensor decomposition methods. In this paper, we derive such conditions for a general class of tensor decomposition methods where each latent tensor component can be reshuffled into a low-rank matrix of arbitrary shape. The reshuffling operation generalizes the traditional unfolding operation, and provides flexibility to recover true latent factors of complex data-structures. We prove that exact recovery can be guaranteed by using a convex program when a type of incoherence measure is upper bounded. The results on image steganography show that our method obtains the state-of-the-art performance. The theoretical analysis in this paper is expected to be useful to derive similar results for other types of tensor-decomposition methods.