HVT: A Comprehensive Vision Framework for Learning in Non-Euclidean Space

Data representation in non-Euclidean spaces has proven effective for capturing hierarchical and complex relationships in real-world datasets. Hyperbolic spaces, in particular, provide efficient embeddings for hierarchical structures. This paper introduces the Hyperbolic Vision Transformer (HVT), a novel extension of the Vision Transformer (ViT) that integrates hyperbolic geometry. While traditional ViTs operate in Euclidean space, our method enhances the self-attention mechanism by leveraging hyperbolic distance and M\"obius transformations. This enables more effective modeling of hierarchical and relational dependencies in image data. We present rigorous mathematical formulations, showing how hyperbolic geometry can be incorporated into attention layers, feed-forward networks, and optimization. We offer improved performance for image classification using the ImageNet dataset.

DIMAT: Decentralized Iterative Merging-And-Training for Deep Learning Models

Recent advances in decentralized deep learning algorithms have demonstrated cutting-edge performance on various tasks with large pre-trained models. However, a pivotal prerequisite for achieving this level of competitiveness is the significant communication and computation overheads when updating these models, which prohibits the applications of them to real-world scenarios. To address this issue, drawing inspiration from advanced model merging techniques without requiring additional training, we introduce the Decentralized Iterative Merging-And-Training (DIMAT) paradigm--a novel decentralized deep learning framework. Within DIMAT, each agent is trained on their local data and periodically merged with their neighboring agents using advanced model merging techniques like activation matching until convergence is achieved. DIMAT provably converges with the best available rate for nonconvex functions with various first-order methods, while yielding tighter error bounds compared to the popular existing approaches. We conduct a comprehensive empirical analysis to validate DIMAT's superiority over baselines across diverse computer vision tasks sourced from multiple datasets. Empirical results validate our theoretical claims by showing that DIMAT attains faster and higher initial gain in accuracy with independent and identically distributed (IID) and non-IID data, incurring lower communication overhead. This DIMAT paradigm presents a new opportunity for the future decentralized learning, enhancing its adaptability to real-world with sparse and light-weight communication and computation.

Robust Concept Erasure Using Task Vectors

With the rapid growth of text-to-image models, a variety of techniques have been suggested to prevent undesirable image generations. Yet, these methods often only protect against specific user prompts and have been shown to allow unsafe generations with other inputs. Here we focus on unconditionally erasing a concept from a text-to-image model rather than conditioning the erasure on the user's prompt. We first show that compared to input-dependent erasure methods, concept erasure that uses Task Vectors (TV) is more robust to unexpected user inputs, not seen during training. However, TV-based erasure can also affect the core performance of the edited model, particularly when the required edit strength is unknown. To this end, we propose a method called Diverse Inversion, which we use to estimate the required strength of the TV edit. Diverse Inversion finds within the model input space a large set of word embeddings, each of which induces the generation of the target concept. We find that encouraging diversity in the set makes our estimation more robust to unexpected prompts. Finally, we show that Diverse Inversion enables us to apply a TV edit only to a subset of the model weights, enhancing the erasure capabilities while better maintaining the core functionality of the model.

LoDIP: Low light phase retrieval with deep image prior

Phase retrieval (PR) is a fundamental challenge in scientific imaging, enabling nanoscale techniques like coherent diffractive imaging (CDI). Imaging at low radiation doses becomes important in applications where samples are susceptible to radiation damage. However, most PR methods struggle in low dose scenario due to the presence of very high shot noise. Advancements in the optical data acquisition setup, exemplified by in-situ CDI, have shown potential for low-dose imaging. But these depend on a time series of measurements, rendering them unsuitable for single-image applications. Similarly, on the computational front, data-driven phase retrieval techniques are not readily adaptable to the single-image context. Deep learning based single-image methods, such as deep image prior, have been effective for various imaging tasks but have exhibited limited success when applied to PR. In this work, we propose LoDIP which combines the in-situ CDI setup with the power of implicit neural priors to tackle the problem of single-image low-dose phase retrieval. Quantitative evaluations demonstrate the superior performance of LoDIP on this task as well as applicability to real experimental scenarios.

Distributionally Robust Classification on a Data Budget

Real world uses of deep learning require predictable model behavior under distribution shifts. Models such as CLIP show emergent natural distributional robustness comparable to humans, but may require hundreds of millions of training samples. Can we train robust learners in a domain where data is limited? To rigorously address this question, we introduce JANuS (Joint Annotations and Names Set), a collection of four new training datasets with images, labels, and corresponding captions, and perform a series of carefully controlled investigations of factors contributing to robustness in image classification, then compare those results to findings derived from a large-scale meta-analysis. Using this approach, we show that standard ResNet-50 trained with the cross-entropy loss on 2.4 million image samples can attain comparable robustness to a CLIP ResNet-50 trained on 400 million samples. To our knowledge, this is the first result showing (near) state-of-the-art distributional robustness on limited data budgets. Our dataset is available at \url{https://huggingface.co/datasets/penfever/JANuS_dataset}, and the code used to reproduce our experiments can be found at \url{https://github.com/penfever/vlhub/}.

Circumventing Concept Erasure Methods For Text-to-Image Generative Models

Text-to-image generative models can produce photo-realistic images for an extremely broad range of concepts, and their usage has proliferated widely among the general public. On the flip side, these models have numerous drawbacks, including their potential to generate images featuring sexually explicit content, mirror artistic styles without permission, or even hallucinate (or deepfake) the likenesses of celebrities. Consequently, various methods have been proposed in order to "erase" sensitive concepts from text-to-image models. In this work, we examine five recently proposed concept erasure methods, and show that targeted concepts are not fully excised from any of these methods. Specifically, we leverage the existence of special learned word embeddings that can retrieve "erased" concepts from the sanitized models with no alterations to their weights. Our results highlight the brittleness of post hoc concept erasure methods, and call into question their use in the algorithmic toolkit for AI safety.

ZeroForge: Feedforward Text-to-Shape Without 3D Supervision

Current state-of-the-art methods for text-to-shape generation either require supervised training using a labeled dataset of pre-defined 3D shapes, or perform expensive inference-time optimization of implicit neural representations. In this work, we present ZeroForge, an approach for zero-shot text-to-shape generation that avoids both pitfalls. To achieve open-vocabulary shape generation, we require careful architectural adaptation of existing feed-forward approaches, as well as a combination of data-free CLIP-loss and contrastive losses to avoid mode collapse. Using these techniques, we are able to considerably expand the generative ability of existing feed-forward text-to-shape models such as CLIP-Forge. We support our method via extensive qualitative and quantitative evaluations

Revisiting Self-Distillation

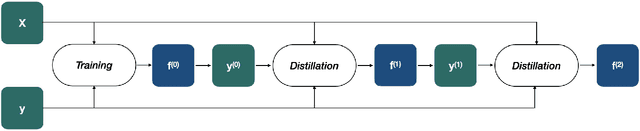
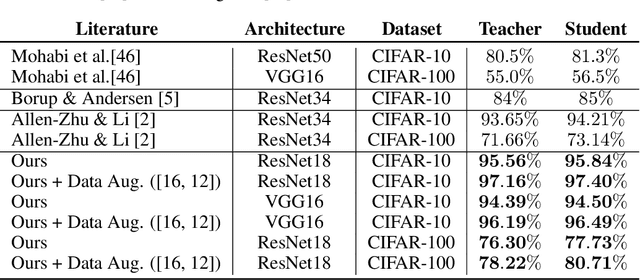
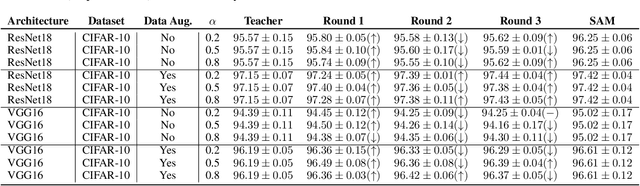
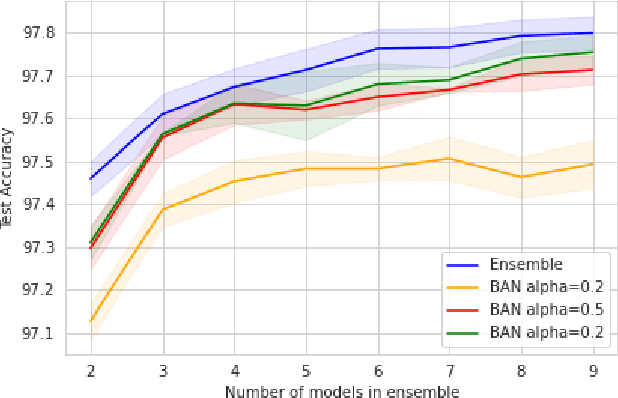
Knowledge distillation is the procedure of transferring "knowledge" from a large model (the teacher) to a more compact one (the student), often being used in the context of model compression. When both models have the same architecture, this procedure is called self-distillation. Several works have anecdotally shown that a self-distilled student can outperform the teacher on held-out data. In this work, we systematically study self-distillation in a number of settings. We first show that even with a highly accurate teacher, self-distillation allows a student to surpass the teacher in all cases. Secondly, we revisit existing theoretical explanations of (self) distillation and identify contradicting examples, revealing possible drawbacks of these explanations. Finally, we provide an alternative explanation for the dynamics of self-distillation through the lens of loss landscape geometry. We conduct extensive experiments to show that self-distillation leads to flatter minima, thereby resulting in better generalization.

Transformer with Fourier Integral Attentions

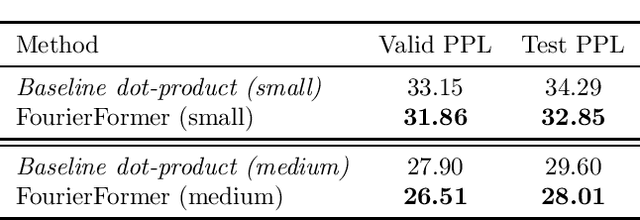
Multi-head attention empowers the recent success of transformers, the state-of-the-art models that have achieved remarkable success in sequence modeling and beyond. These attention mechanisms compute the pairwise dot products between the queries and keys, which results from the use of unnormalized Gaussian kernels with the assumption that the queries follow a mixture of Gaussian distribution. There is no guarantee that this assumption is valid in practice. In response, we first interpret attention in transformers as a nonparametric kernel regression. We then propose the FourierFormer, a new class of transformers in which the dot-product kernels are replaced by the novel generalized Fourier integral kernels. Different from the dot-product kernels, where we need to choose a good covariance matrix to capture the dependency of the features of data, the generalized Fourier integral kernels can automatically capture such dependency and remove the need to tune the covariance matrix. We theoretically prove that our proposed Fourier integral kernels can efficiently approximate any key and query distributions. Compared to the conventional transformers with dot-product attention, FourierFormers attain better accuracy and reduce the redundancy between attention heads. We empirically corroborate the advantages of FourierFormers over the baseline transformers in a variety of practical applications including language modeling and image classification.

Smooth-Reduce: Leveraging Patches for Improved Certified Robustness

Randomized smoothing (RS) has been shown to be a fast, scalable technique for certifying the robustness of deep neural network classifiers. However, methods based on RS require augmenting data with large amounts of noise, which leads to significant drops in accuracy. We propose a training-free, modified smoothing approach, Smooth-Reduce, that leverages patching and aggregation to provide improved classifier certificates. Our algorithm classifies overlapping patches extracted from an input image, and aggregates the predicted logits to certify a larger radius around the input. We study two aggregation schemes -- max and mean -- and show that both approaches provide better certificates in terms of certified accuracy, average certified radii and abstention rates as compared to concurrent approaches. We also provide theoretical guarantees for such certificates, and empirically show significant improvements over other randomized smoothing methods that require expensive retraining. Further, we extend our approach to videos and provide meaningful certificates for video classifiers. A project page can be found at https://nyu-dice-lab.github.io/SmoothReduce/