Looping in the Human: Collaborative and Explainable Bayesian Optimization

Like many optimizers, Bayesian optimization often falls short of gaining user trust due to opacity. While attempts have been made to develop human-centric optimizers, they typically assume user knowledge is well-specified and error-free, employing users mainly as supervisors of the optimization process. We relax these assumptions and propose a more balanced human-AI partnership with our Collaborative and Explainable Bayesian Optimization (CoExBO) framework. Instead of explicitly requiring a user to provide a knowledge model, CoExBO employs preference learning to seamlessly integrate human insights into the optimization, resulting in algorithmic suggestions that resonate with user preference. CoExBO explains its candidate selection every iteration to foster trust, empowering users with a clearer grasp of the optimization. Furthermore, CoExBO offers a no-harm guarantee, allowing users to make mistakes; even with extreme adversarial interventions, the algorithm converges asymptotically to a vanilla Bayesian optimization. We validate CoExBO's efficacy through human-AI teaming experiments in lithium-ion battery design, highlighting substantial improvements over conventional methods.

Domain-Agnostic Batch Bayesian Optimization with Diverse Constraints via Bayesian Quadrature

Real-world optimisation problems often feature complex combinations of (1) diverse constraints, (2) discrete and mixed spaces, and are (3) highly parallelisable. (4) There are also cases where the objective function cannot be queried if unknown constraints are not satisfied, e.g. in drug discovery, safety on animal experiments (unknown constraints) must be established before human clinical trials (querying objective function) may proceed. However, most existing works target each of the above three problems in isolation and do not consider (4) unknown constraints with query rejection. For problems with diverse constraints and/or unconventional input spaces, it is difficult to apply these techniques as they are often mutually incompatible. We propose cSOBER, a domain-agnostic prudent parallel active sampler for Bayesian optimisation, based on SOBER of Adachi et al. (2023). We consider infeasibility under unknown constraints as a type of integration error that we can estimate. We propose a theoretically-driven approach that propagates such error as a tolerance in the quadrature precision that automatically balances exploitation and exploration with the expected rejection rate. Moreover, our method flexibly accommodates diverse constraints and/or discrete and mixed spaces via adaptive tolerance, including conventional zero-risk cases. We show that cSOBER outperforms competitive baselines on diverse real-world blackbox-constrained problems, including safety-constrained drug discovery, and human-relationship-aware team optimisation over graph-structured space.

Bayesian Optimisation of Functions on Graphs

The increasing availability of graph-structured data motivates the task of optimising over functions defined on the node set of graphs. Traditional graph search algorithms can be applied in this case, but they may be sample-inefficient and do not make use of information about the function values; on the other hand, Bayesian optimisation is a class of promising black-box solvers with superior sample efficiency, but it has been scarcely been applied to such novel setups. To fill this gap, we propose a novel Bayesian optimisation framework that optimises over functions defined on generic, large-scale and potentially unknown graphs. Through the learning of suitable kernels on graphs, our framework has the advantage of adapting to the behaviour of the target function. The local modelling approach further guarantees the efficiency of our method. Extensive experiments on both synthetic and real-world graphs demonstrate the effectiveness of the proposed optimisation framework.

On Pathologies in KL-Regularized Reinforcement Learning from Expert Demonstrations

KL-regularized reinforcement learning from expert demonstrations has proved successful in improving the sample efficiency of deep reinforcement learning algorithms, allowing them to be applied to challenging physical real-world tasks. However, we show that KL-regularized reinforcement learning with behavioral reference policies derived from expert demonstrations can suffer from pathological training dynamics that can lead to slow, unstable, and suboptimal online learning. We show empirically that the pathology occurs for commonly chosen behavioral policy classes and demonstrate its impact on sample efficiency and online policy performance. Finally, we show that the pathology can be remedied by non-parametric behavioral reference policies and that this allows KL-regularized reinforcement learning to significantly outperform state-of-the-art approaches on a variety of challenging locomotion and dexterous hand manipulation tasks.

Bayesian Model Selection of Lithium-Ion Battery Models via Bayesian Quadrature

A wide variety of battery models are available, and it is not always obvious which model `best' describes a dataset. This paper presents a Bayesian model selection approach using Bayesian quadrature. The model evidence is adopted as the selection metric, choosing the simplest model that describes the data, in the spirit of Occam's razor. However, estimating this requires integral computations over parameter space, which is usually prohibitively expensive. Bayesian quadrature offers sample-efficient integration via model-based inference that minimises the number of battery model evaluations. The posterior distribution of model parameters can also be inferred as a byproduct without further computation. Here, the simplest lithium-ion battery models, equivalent circuit models, were used to analyse the sensitivity of the selection criterion to given different datasets and model configurations. We show that popular model selection criteria, such as root-mean-square error and Bayesian information criterion, can fail to select a parsimonious model in the case of a multimodal posterior. The model evidence can spot the optimal model in such cases, simultaneously providing the variance of the evidence inference itself as an indication of confidence. We also show that Bayesian quadrature can compute the evidence faster than popular Monte Carlo based solvers.

Bayesian Optimization over Discrete and Mixed Spaces via Probabilistic Reparameterization

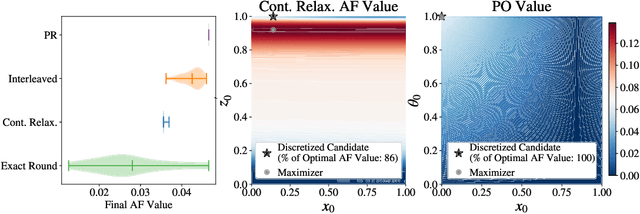
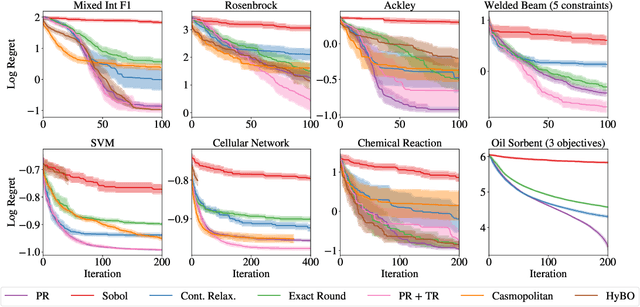
Optimizing expensive-to-evaluate black-box functions of discrete (and potentially continuous) design parameters is a ubiquitous problem in scientific and engineering applications. Bayesian optimization (BO) is a popular, sample-efficient method that leverages a probabilistic surrogate model and an acquisition function (AF) to select promising designs to evaluate. However, maximizing the AF over mixed or high-cardinality discrete search spaces is challenging standard gradient-based methods cannot be used directly or evaluating the AF at every point in the search space would be computationally prohibitive. To address this issue, we propose using probabilistic reparameterization (PR). Instead of directly optimizing the AF over the search space containing discrete parameters, we instead maximize the expectation of the AF over a probability distribution defined by continuous parameters. We prove that under suitable reparameterizations, the BO policy that maximizes the probabilistic objective is the same as that which maximizes the AF, and therefore, PR enjoys the same regret bounds as the original BO policy using the underlying AF. Moreover, our approach provably converges to a stationary point of the probabilistic objective under gradient ascent using scalable, unbiased estimators of both the probabilistic objective and its gradient. Therefore, as the number of starting points and gradient steps increase, our approach will recover of a maximizer of the AF (an often-neglected requisite for commonly used BO regret bounds). We validate our approach empirically and demonstrate state-of-the-art optimization performance on a wide range of real-world applications. PR is complementary to (and benefits) recent work and naturally generalizes to settings with multiple objectives and black-box constraints.

Log-Linear-Time Gaussian Processes Using Binary Tree Kernels

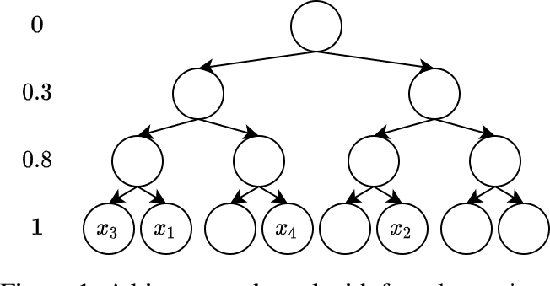
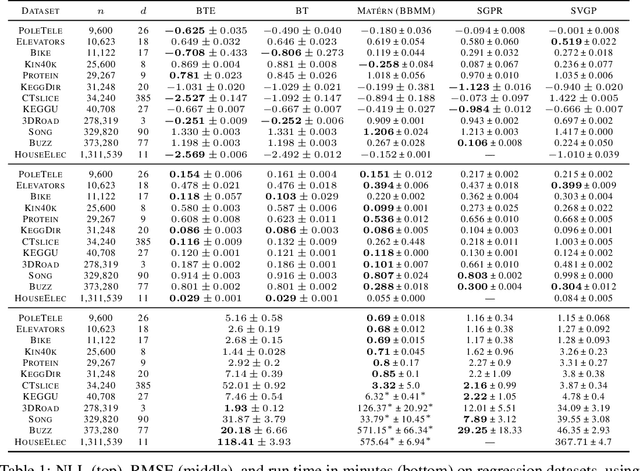
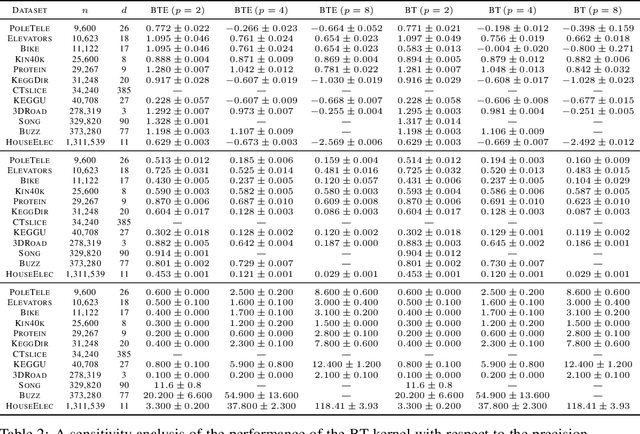
Gaussian processes (GPs) produce good probabilistic models of functions, but most GP kernels require $O((n+m)n^2)$ time, where $n$ is the number of data points and $m$ the number of predictive locations. We present a new kernel that allows for Gaussian process regression in $O((n+m)\log(n+m))$ time. Our "binary tree" kernel places all data points on the leaves of a binary tree, with the kernel depending only on the depth of the deepest common ancestor. We can store the resulting kernel matrix in $O(n)$ space in $O(n \log n)$ time, as a sum of sparse rank-one matrices, and approximately invert the kernel matrix in $O(n)$ time. Sparse GP methods also offer linear run time, but they predict less well than higher dimensional kernels. On a classic suite of regression tasks, we compare our kernel against Mat\'ern, sparse, and sparse variational kernels. The binary tree GP assigns the highest likelihood to the test data on a plurality of datasets, usually achieves lower mean squared error than the sparse methods, and often ties or beats the Mat\'ern GP. On large datasets, the binary tree GP is fastest, and much faster than a Mat\'ern GP.

Bayesian Generational Population-Based Training

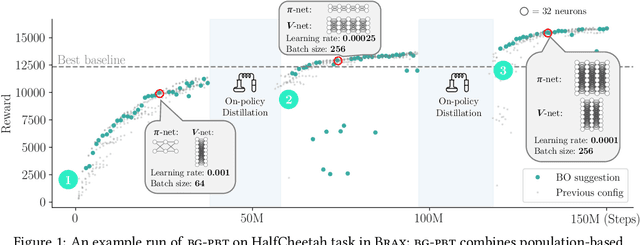
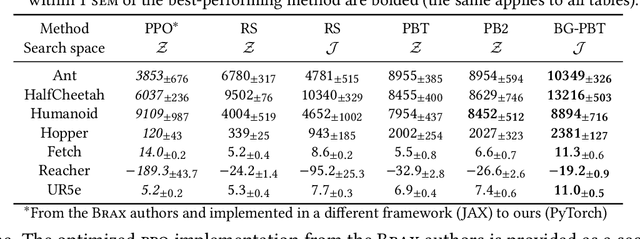
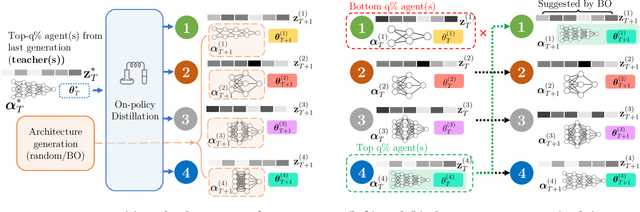
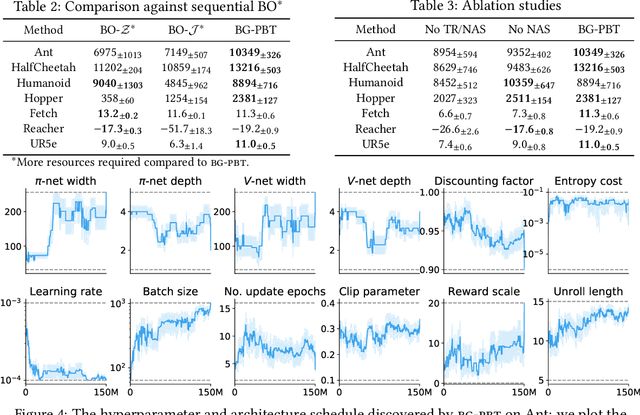
Reinforcement learning (RL) offers the potential for training generally capable agents that can interact autonomously in the real world. However, one key limitation is the brittleness of RL algorithms to core hyperparameters and network architecture choice. Furthermore, non-stationarities such as evolving training data and increased agent complexity mean that different hyperparameters and architectures may be optimal at different points of training. This motivates AutoRL, a class of methods seeking to automate these design choices. One prominent class of AutoRL methods is Population-Based Training (PBT), which have led to impressive performance in several large scale settings. In this paper, we introduce two new innovations in PBT-style methods. First, we employ trust-region based Bayesian Optimization, enabling full coverage of the high-dimensional mixed hyperparameter search space. Second, we show that using a generational approach, we can also learn both architectures and hyperparameters jointly on-the-fly in a single training run. Leveraging the new highly parallelizable Brax physics engine, we show that these innovations lead to large performance gains, significantly outperforming the tuned baseline while learning entire configurations on the fly. Code is available at https://github.com/xingchenwan/bgpbt.

Challenges and Opportunities in Offline Reinforcement Learning from Visual Observations

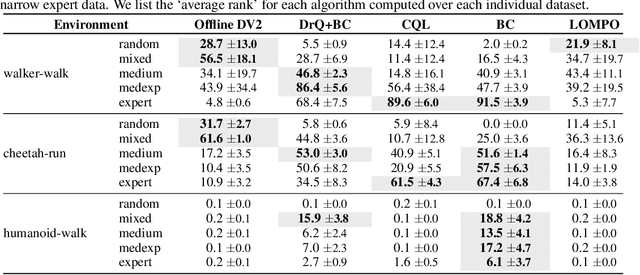
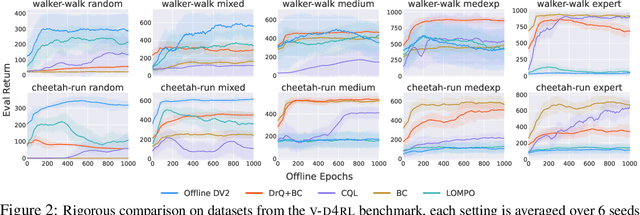
Offline reinforcement learning has shown great promise in leveraging large pre-collected datasets for policy learning, allowing agents to forgo often-expensive online data collection. However, to date, offline reinforcement learning from has been relatively under-explored, and there is a lack of understanding of where the remaining challenges lie. In this paper, we seek to establish simple baselines for continuous control in the visual domain. We show that simple modifications to two state-of-the-art vision-based online reinforcement learning algorithms, DreamerV2 and DrQ-v2, suffice to outperform prior work and establish a competitive baseline. We rigorously evaluate these algorithms on both existing offline datasets and a new testbed for offline reinforcement learning from visual observations that better represents the data distributions present in real-world offline reinforcement learning problems, and open-source our code and data to facilitate progress in this important domain. Finally, we present and analyze several key desiderata unique to offline RL from visual observations, including visual distractions and visually identifiable changes in dynamics.

Fast Bayesian Inference with Batch Bayesian Quadrature via Kernel Recombination

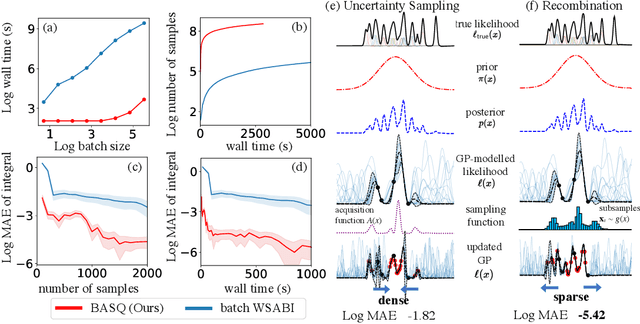
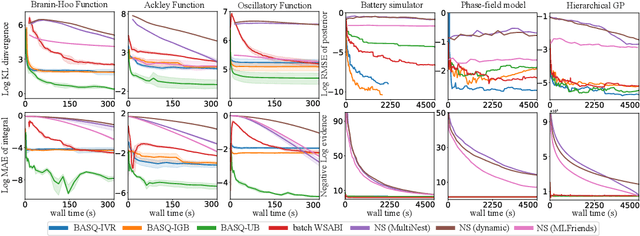
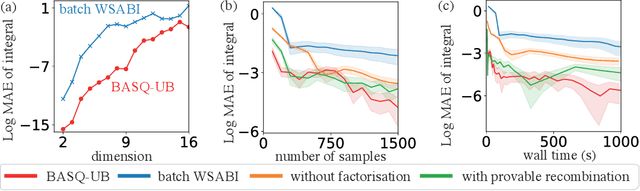
Calculation of Bayesian posteriors and model evidences typically requires numerical integration. Bayesian quadrature (BQ), a surrogate-model-based approach to numerical integration, is capable of superb sample efficiency, but its lack of parallelisation has hindered its practical applications. In this work, we propose a parallelised (batch) BQ method, employing techniques from kernel quadrature, that possesses a provably-exponential convergence rate. Additionally, just as with Nested Sampling, our method permits simultaneous inference of both posteriors and model evidence. Samples from our BQ surrogate model are re-selected to give a sparse set of samples, via a kernel recombination algorithm, requiring negligible additional time to increase the batch size. Empirically, we find that our approach significantly outperforms the sampling efficiency of both state-of-the-art BQ techniques and Nested Sampling in various real-world datasets, including lithium-ion battery analytics.