Scalable Gaussian Processes with Latent Kronecker Structure

Applying Gaussian processes (GPs) to very large datasets remains a challenge due to limited computational scalability. Matrix structures, such as the Kronecker product, can accelerate operations significantly, but their application commonly entails approximations or unrealistic assumptions. In particular, the most common path to creating a Kronecker-structured kernel matrix is by evaluating a product kernel on gridded inputs that can be expressed as a Cartesian product. However, this structure is lost if any observation is missing, breaking the Cartesian product structure, which frequently occurs in real-world data such as time series. To address this limitation, we propose leveraging latent Kronecker structure, by expressing the kernel matrix of observed values as the projection of a latent Kronecker product. In combination with iterative linear system solvers and pathwise conditioning, our method facilitates inference of exact GPs while requiring substantially fewer computational resources than standard iterative methods. We demonstrate that our method outperforms state-of-the-art sparse and variational GPs on real-world datasets with up to five million examples, including robotics, automated machine learning, and climate applications.

Robust Gaussian Processes via Relevance Pursuit

Gaussian processes (GPs) are non-parametric probabilistic regression models that are popular due to their flexibility, data efficiency, and well-calibrated uncertainty estimates. However, standard GP models assume homoskedastic Gaussian noise, while many real-world applications are subject to non-Gaussian corruptions. Variants of GPs that are more robust to alternative noise models have been proposed, and entail significant trade-offs between accuracy and robustness, and between computational requirements and theoretical guarantees. In this work, we propose and study a GP model that achieves robustness against sparse outliers by inferring data-point-specific noise levels with a sequential selection procedure maximizing the log marginal likelihood that we refer to as relevance pursuit. We show, surprisingly, that the model can be parameterized such that the associated log marginal likelihood is strongly concave in the data-point-specific noise variances, a property rarely found in either robust regression objectives or GP marginal likelihoods. This in turn implies the weak submodularity of the corresponding subset selection problem, and thereby proves approximation guarantees for the proposed algorithm. We compare the model's performance relative to other approaches on diverse regression and Bayesian optimization tasks, including the challenging but common setting of sparse corruptions of the labels within or close to the function range.

Sample-Efficient Bayesian Optimization with Transfer Learning for Heterogeneous Search Spaces

Bayesian optimization (BO) is a powerful approach to sample-efficient optimization of black-box functions. However, in settings with very few function evaluations, a successful application of BO may require transferring information from historical experiments. These related experiments may not have exactly the same tunable parameters (search spaces), motivating the need for BO with transfer learning for heterogeneous search spaces. In this paper, we propose two methods for this setting. The first approach leverages a Gaussian process (GP) model with a conditional kernel to transfer information between different search spaces. Our second approach treats the missing parameters as hyperparameters of the GP model that can be inferred jointly with the other GP hyperparameters or set to fixed values. We show that these two methods perform well on several benchmark problems.

Approximation-Aware Bayesian Optimization

High-dimensional Bayesian optimization (BO) tasks such as molecular design often require 10,000 function evaluations before obtaining meaningful results. While methods like sparse variational Gaussian processes (SVGPs) reduce computational requirements in these settings, the underlying approximations result in suboptimal data acquisitions that slow the progress of optimization. In this paper we modify SVGPs to better align with the goals of BO: targeting informed data acquisition rather than global posterior fidelity. Using the framework of utility-calibrated variational inference, we unify GP approximation and data acquisition into a joint optimization problem, thereby ensuring optimal decisions under a limited computational budget. Our approach can be used with any decision-theoretic acquisition function and is compatible with trust region methods like TuRBO. We derive efficient joint objectives for the expected improvement and knowledge gradient acquisition functions in both the standard and batch BO settings. Our approach outperforms standard SVGPs on high-dimensional benchmark tasks in control and molecular design.

Unexpected Improvements to Expected Improvement for Bayesian Optimization

Expected Improvement (EI) is arguably the most popular acquisition function in Bayesian optimization and has found countless successful applications, but its performance is often exceeded by that of more recent methods. Notably, EI and its variants, including for the parallel and multi-objective settings, are challenging to optimize because their acquisition values vanish numerically in many regions. This difficulty generally increases as the number of observations, dimensionality of the search space, or the number of constraints grow, resulting in performance that is inconsistent across the literature and most often sub-optimal. Herein, we propose LogEI, a new family of acquisition functions whose members either have identical or approximately equal optima as their canonical counterparts, but are substantially easier to optimize numerically. We demonstrate that numerical pathologies manifest themselves in "classic" analytic EI, Expected Hypervolume Improvement (EHVI), as well as their constrained, noisy, and parallel variants, and propose corresponding reformulations that remedy these pathologies. Our empirical results show that members of the LogEI family of acquisition functions substantially improve on the optimization performance of their canonical counterparts and surprisingly, are on par with or exceed the performance of recent state-of-the-art acquisition functions, highlighting the understated role of numerical optimization in the literature.

Bayesian Optimization over High-Dimensional Combinatorial Spaces via Dictionary-based Embeddings

We consider the problem of optimizing expensive black-box functions over high-dimensional combinatorial spaces which arises in many science, engineering, and ML applications. We use Bayesian Optimization (BO) and propose a novel surrogate modeling approach for efficiently handling a large number of binary and categorical parameters. The key idea is to select a number of discrete structures from the input space (the dictionary) and use them to define an ordinal embedding for high-dimensional combinatorial structures. This allows us to use existing Gaussian process models for continuous spaces. We develop a principled approach based on binary wavelets to construct dictionaries for binary spaces, and propose a randomized construction method that generalizes to categorical spaces. We provide theoretical justification to support the effectiveness of the dictionary-based embeddings. Our experiments on diverse real-world benchmarks demonstrate the effectiveness of our proposed surrogate modeling approach over state-of-the-art BO methods.

Bayesian Optimization over Discrete and Mixed Spaces via Probabilistic Reparameterization

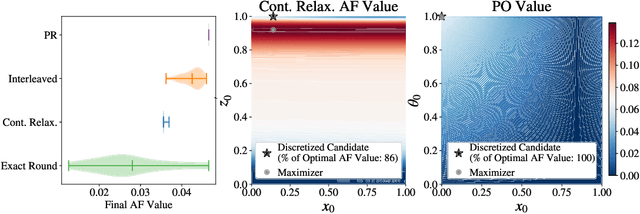
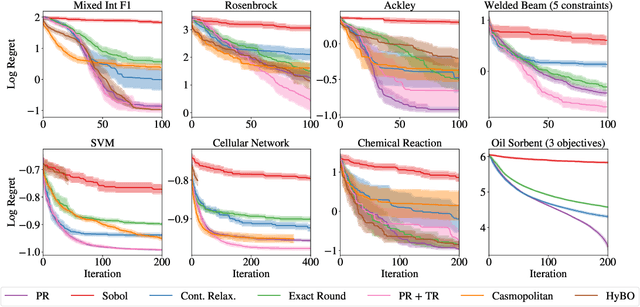
Optimizing expensive-to-evaluate black-box functions of discrete (and potentially continuous) design parameters is a ubiquitous problem in scientific and engineering applications. Bayesian optimization (BO) is a popular, sample-efficient method that leverages a probabilistic surrogate model and an acquisition function (AF) to select promising designs to evaluate. However, maximizing the AF over mixed or high-cardinality discrete search spaces is challenging standard gradient-based methods cannot be used directly or evaluating the AF at every point in the search space would be computationally prohibitive. To address this issue, we propose using probabilistic reparameterization (PR). Instead of directly optimizing the AF over the search space containing discrete parameters, we instead maximize the expectation of the AF over a probability distribution defined by continuous parameters. We prove that under suitable reparameterizations, the BO policy that maximizes the probabilistic objective is the same as that which maximizes the AF, and therefore, PR enjoys the same regret bounds as the original BO policy using the underlying AF. Moreover, our approach provably converges to a stationary point of the probabilistic objective under gradient ascent using scalable, unbiased estimators of both the probabilistic objective and its gradient. Therefore, as the number of starting points and gradient steps increase, our approach will recover of a maximizer of the AF (an often-neglected requisite for commonly used BO regret bounds). We validate our approach empirically and demonstrate state-of-the-art optimization performance on a wide range of real-world applications. PR is complementary to (and benefits) recent work and naturally generalizes to settings with multiple objectives and black-box constraints.

Sparse Bayesian Optimization

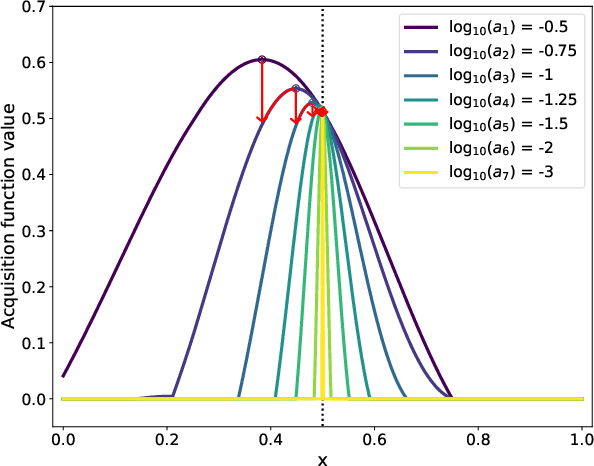
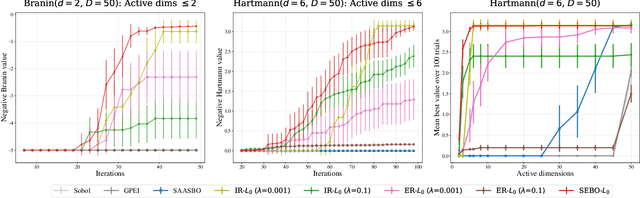
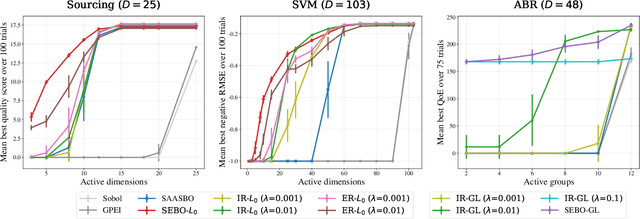
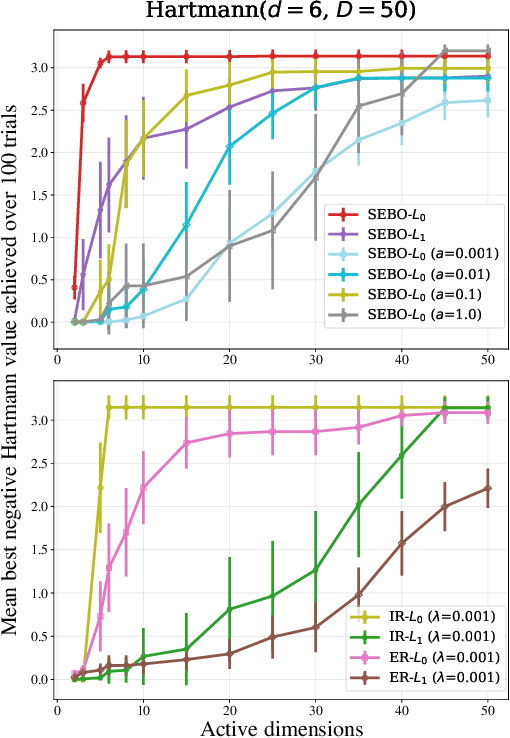
Bayesian optimization (BO) is a powerful approach to sample-efficient optimization of black-box objective functions. However, the application of BO to areas such as recommendation systems often requires taking the interpretability and simplicity of the configurations into consideration, a setting that has not been previously studied in the BO literature. To make BO applicable in this setting, we present several regularization-based approaches that allow us to discover sparse and more interpretable configurations. We propose a novel differentiable relaxation based on homotopy continuation that makes it possible to target sparsity by working directly with $L_0$ regularization. We identify failure modes for regularized BO and develop a hyperparameter-free method, sparsity exploring Bayesian optimization (SEBO) that seeks to simultaneously maximize a target objective and sparsity. SEBO and methods based on fixed regularization are evaluated on synthetic and real-world problems, and we show that we are able to efficiently optimize for sparsity.

Multi-Objective Bayesian Optimization over High-Dimensional Search Spaces

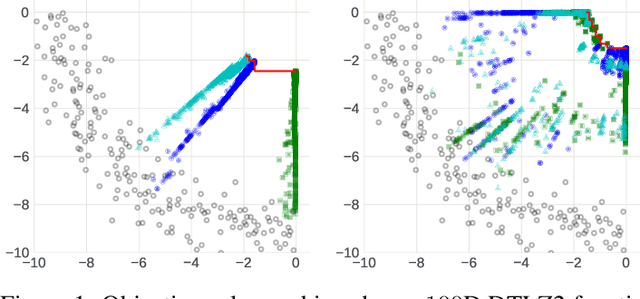
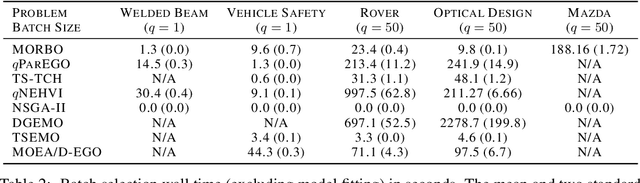
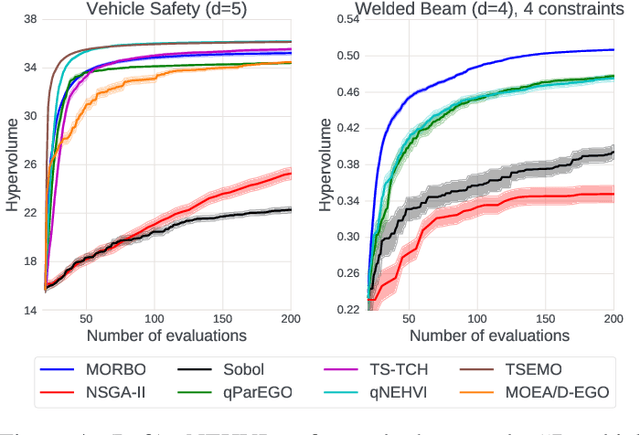
The ability to optimize multiple competing objective functions with high sample efficiency is imperative in many applied problems across science and industry. Multi-objective Bayesian optimization (BO) achieves strong empirical performance on such problems, but even with recent methodological advances, it has been restricted to simple, low-dimensional domains. Most existing BO methods exhibit poor performance on search spaces with more than a few dozen parameters. In this work we propose MORBO, a method for multi-objective Bayesian optimization over high-dimensional search spaces. MORBO performs local Bayesian optimization within multiple trust regions simultaneously, allowing it to explore and identify diverse solutions even when the objective functions are difficult to model globally. We show that MORBO significantly advances the state-of-the-art in sample-efficiency for several high-dimensional synthetic and real-world multi-objective problems, including a vehicle design problem with 222 parameters, demonstrating that MORBO is a practical approach for challenging and important problems that were previously out of reach for BO methods.

Latency-Aware Neural Architecture Search with Multi-Objective Bayesian Optimization

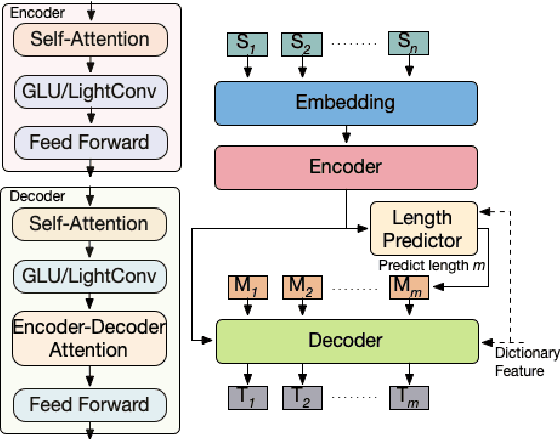
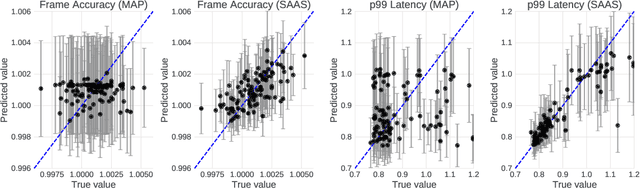
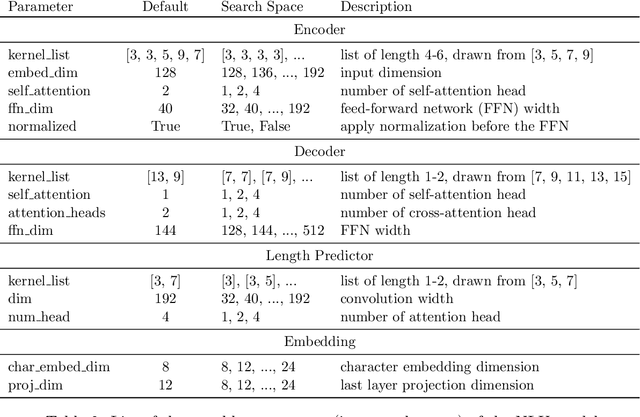
When tuning the architecture and hyperparameters of large machine learning models for on-device deployment, it is desirable to understand the optimal trade-offs between on-device latency and model accuracy. In this work, we leverage recent methodological advances in Bayesian optimization over high-dimensional search spaces and multi-objective Bayesian optimization to efficiently explore these trade-offs for a production-scale on-device natural language understanding model at Facebook.