Log-Linear-Time Gaussian Processes Using Binary Tree Kernels
Paper and Code
Oct 04, 2022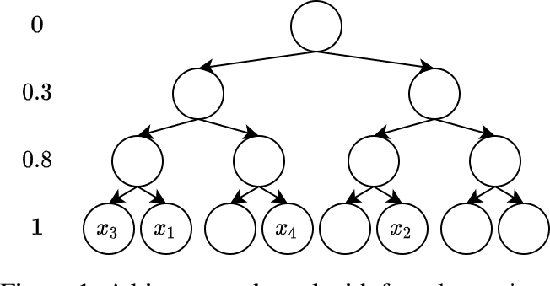
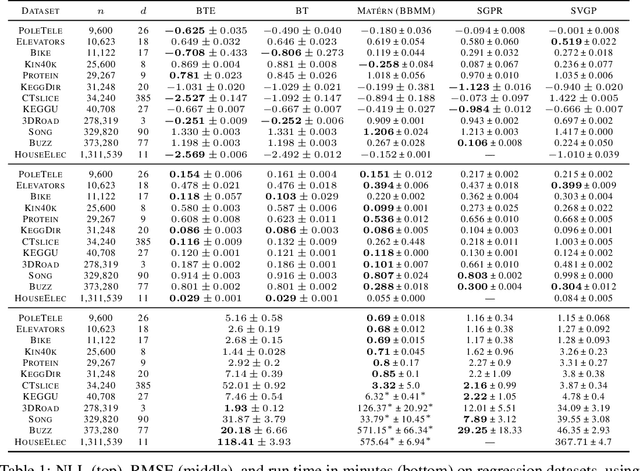
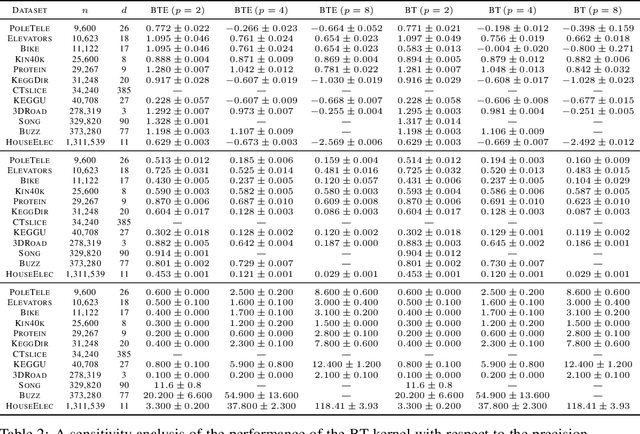
Gaussian processes (GPs) produce good probabilistic models of functions, but most GP kernels require $O((n+m)n^2)$ time, where $n$ is the number of data points and $m$ the number of predictive locations. We present a new kernel that allows for Gaussian process regression in $O((n+m)\log(n+m))$ time. Our "binary tree" kernel places all data points on the leaves of a binary tree, with the kernel depending only on the depth of the deepest common ancestor. We can store the resulting kernel matrix in $O(n)$ space in $O(n \log n)$ time, as a sum of sparse rank-one matrices, and approximately invert the kernel matrix in $O(n)$ time. Sparse GP methods also offer linear run time, but they predict less well than higher dimensional kernels. On a classic suite of regression tasks, we compare our kernel against Mat\'ern, sparse, and sparse variational kernels. The binary tree GP assigns the highest likelihood to the test data on a plurality of datasets, usually achieves lower mean squared error than the sparse methods, and often ties or beats the Mat\'ern GP. On large datasets, the binary tree GP is fastest, and much faster than a Mat\'ern GP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge