Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

RL, but don't do anything I wouldn't do

In reinforcement learning, if the agent's reward differs from the designers' true utility, even only rarely, the state distribution resulting from the agent's policy can be very bad, in theory and in practice. When RL policies would devolve into undesired behavior, a common countermeasure is KL regularization to a trusted policy ("Don't do anything I wouldn't do"). All current cutting-edge language models are RL agents that are KL-regularized to a "base policy" that is purely predictive. Unfortunately, we demonstrate that when this base policy is a Bayesian predictive model of a trusted policy, the KL constraint is no longer reliable for controlling the behavior of an advanced RL agent. We demonstrate this theoretically using algorithmic information theory, and while systems today are too weak to exhibit this theorized failure precisely, we RL-finetune a language model and find evidence that our formal results are plausibly relevant in practice. We also propose a theoretical alternative that avoids this problem by replacing the "Don't do anything I wouldn't do" principle with "Don't do anything I mightn't do".

Can a Bayesian Oracle Prevent Harm from an Agent?

Is there a way to design powerful AI systems based on machine learning methods that would satisfy probabilistic safety guarantees? With the long-term goal of obtaining a probabilistic guarantee that would apply in every context, we consider estimating a context-dependent bound on the probability of violating a given safety specification. Such a risk evaluation would need to be performed at run-time to provide a guardrail against dangerous actions of an AI. Noting that different plausible hypotheses about the world could produce very different outcomes, and because we do not know which one is right, we derive bounds on the safety violation probability predicted under the true but unknown hypothesis. Such bounds could be used to reject potentially dangerous actions. Our main results involve searching for cautious but plausible hypotheses, obtained by a maximization that involves Bayesian posteriors over hypotheses. We consider two forms of this result, in the iid case and in the non-iid case, and conclude with open problems towards turning such theoretical results into practical AI guardrails.

Log-Linear-Time Gaussian Processes Using Binary Tree Kernels

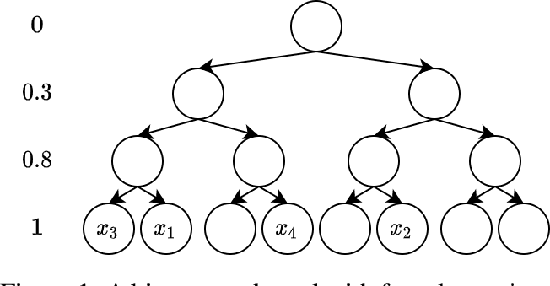
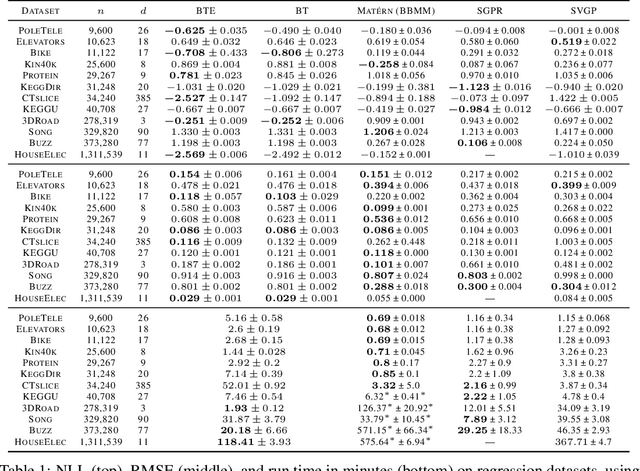
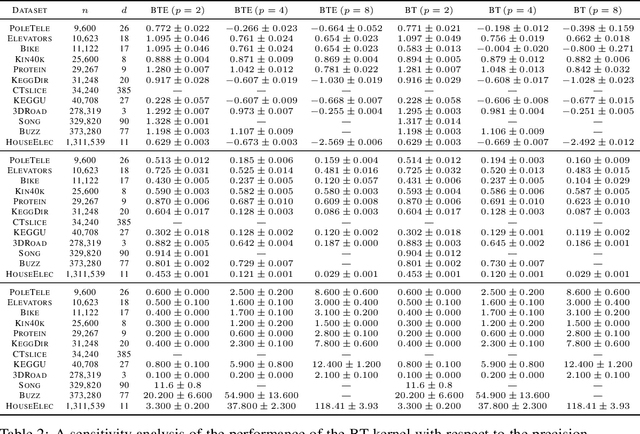
Gaussian processes (GPs) produce good probabilistic models of functions, but most GP kernels require $O((n+m)n^2)$ time, where $n$ is the number of data points and $m$ the number of predictive locations. We present a new kernel that allows for Gaussian process regression in $O((n+m)\log(n+m))$ time. Our "binary tree" kernel places all data points on the leaves of a binary tree, with the kernel depending only on the depth of the deepest common ancestor. We can store the resulting kernel matrix in $O(n)$ space in $O(n \log n)$ time, as a sum of sparse rank-one matrices, and approximately invert the kernel matrix in $O(n)$ time. Sparse GP methods also offer linear run time, but they predict less well than higher dimensional kernels. On a classic suite of regression tasks, we compare our kernel against Mat\'ern, sparse, and sparse variational kernels. The binary tree GP assigns the highest likelihood to the test data on a plurality of datasets, usually achieves lower mean squared error than the sparse methods, and often ties or beats the Mat\'ern GP. On large datasets, the binary tree GP is fastest, and much faster than a Mat\'ern GP.

Intelligence and Unambitiousness Using Algorithmic Information Theory

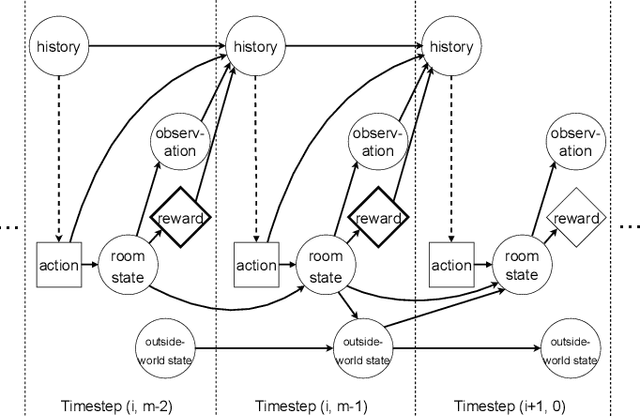
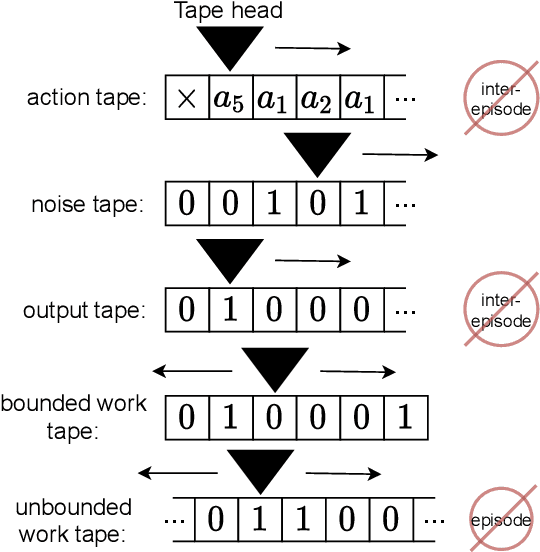
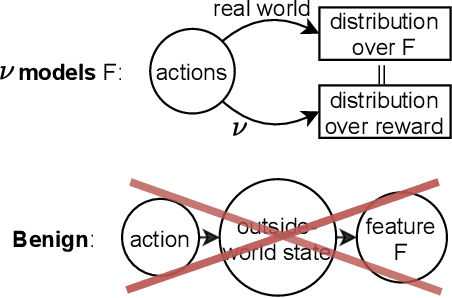
Algorithmic Information Theory has inspired intractable constructions of general intelligence (AGI), and undiscovered tractable approximations are likely feasible. Reinforcement Learning (RL), the dominant paradigm by which an agent might learn to solve arbitrary solvable problems, gives an agent a dangerous incentive: to gain arbitrary "power" in order to intervene in the provision of their own reward. We review the arguments that generally intelligent algorithmic-information-theoretic reinforcement learners such as Hutter's (2005) AIXI would seek arbitrary power, including over us. Then, using an information-theoretic exploration schedule, and a setup inspired by causal influence theory, we present a variant of AIXI which learns to not seek arbitrary power; we call it "unambitious". We show that our agent learns to accrue reward at least as well as a human mentor, while relying on that mentor with diminishing probability. And given a formal assumption that we probe empirically, we show that eventually, the agent's world-model incorporates the following true fact: intervening in the "outside world" will have no effect on reward acquisition; hence, it has no incentive to shape the outside world.

Fully General Online Imitation Learning

In imitation learning, imitators and demonstrators are policies for picking actions given past interactions with the environment. If we run an imitator, we probably want events to unfold similarly to the way they would have if the demonstrator had been acting the whole time. No existing work provides formal guidance in how this might be accomplished, instead restricting focus to environments that restart, making learning unusually easy, and conveniently limiting the significance of any mistake. We address a fully general setting, in which the (stochastic) environment and demonstrator never reset, not even for training purposes. Our new conservative Bayesian imitation learner underestimates the probabilities of each available action, and queries for more data with the remaining probability. Our main result: if an event would have been unlikely had the demonstrator acted the whole time, that event's likelihood can be bounded above when running the (initially totally ignorant) imitator instead. Meanwhile, queries to the demonstrator rapidly diminish in frequency.

Pessimism About Unknown Unknowns Inspires Conservatism

If we could define the set of all bad outcomes, we could hard-code an agent which avoids them; however, in sufficiently complex environments, this is infeasible. We do not know of any general-purpose approaches in the literature to avoiding novel failure modes. Motivated by this, we define an idealized Bayesian reinforcement learner which follows a policy that maximizes the worst-case expected reward over a set of world-models. We call this agent pessimistic, since it optimizes assuming the worst case. A scalar parameter tunes the agent's pessimism by changing the size of the set of world-models taken into account. Our first main contribution is: given an assumption about the agent's model class, a sufficiently pessimistic agent does not cause "unprecedented events" with probability $1-\delta$, whether or not designers know how to precisely specify those precedents they are concerned with. Since pessimism discourages exploration, at each timestep, the agent may defer to a mentor, who may be a human or some known-safe policy we would like to improve. Our other main contribution is that the agent's policy's value approaches at least that of the mentor, while the probability of deferring to the mentor goes to 0. In high-stakes environments, we might like advanced artificial agents to pursue goals cautiously, which is a non-trivial problem even if the agent were allowed arbitrary computing power; we present a formal solution.

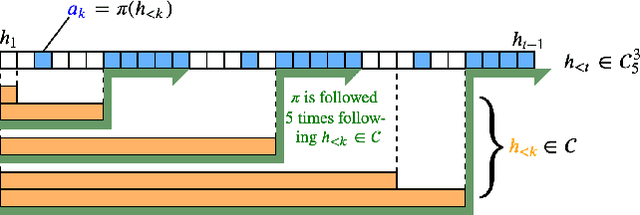
Curiosity Killed the Cat and the Asymptotically Optimal Agent

Reinforcement learners are agents that learn to pick actions that lead to high reward. Ideally, the value of a reinforcement learner's policy approaches optimality--where the optimal informed policy is the one which maximizes reward. Unfortunately, we show that if an agent is guaranteed to be "asymptotically optimal" in any (stochastically computable) environment, then subject to an assumption about the true environment, this agent will be either destroyed or incapacitated with probability 1; both of these are forms of traps as understood in the Markov Decision Process literature. Environments with traps pose a well-known problem for agents, but we are unaware of other work which shows that traps are not only a risk, but a certainty, for agents of a certain caliber. Much work in reinforcement learning uses an ergodicity assumption to avoid this problem. Often, doing theoretical research under simplifying assumptions prepares us to provide practical solutions even in the absence of those assumptions, but the ergodicity assumption in reinforcement learning may have led us entirely astray in preparing safe and effective exploration strategies for agents in dangerous environments. Rather than assuming away the problem, we present an agent with the modest guarantee of approaching the performance of a mentor, doing safe exploration instead of reckless exploration.

Strong Asymptotic Optimality in General Environments

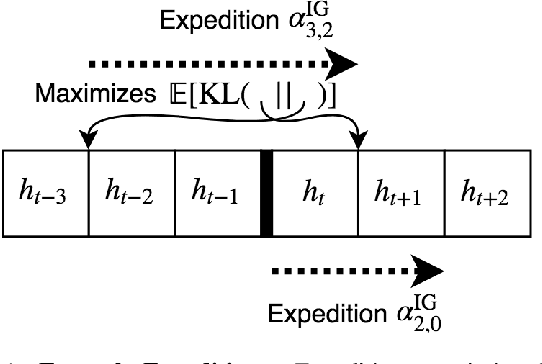
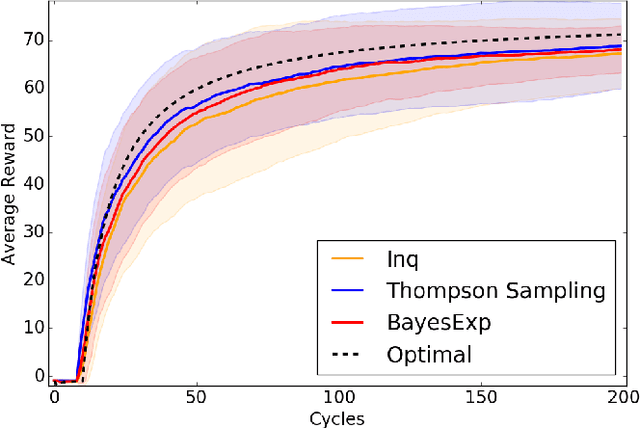
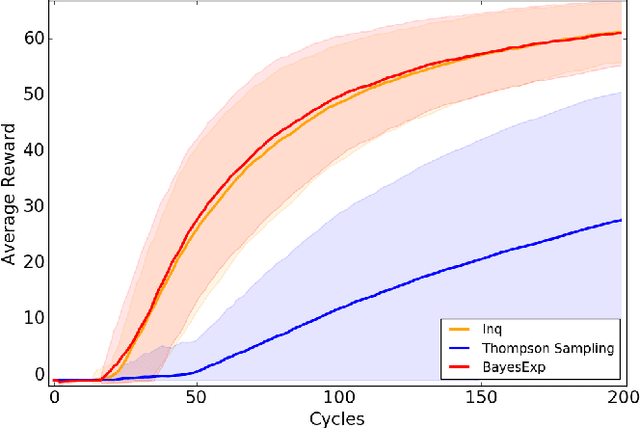
Reinforcement Learning agents are expected to eventually perform well. Typically, this takes the form of a guarantee about the asymptotic behavior of an algorithm given some assumptions about the environment. We present an algorithm for a policy whose value approaches the optimal value with probability 1 in all computable probabilistic environments, provided the agent has a bounded horizon. This is known as strong asymptotic optimality, and it was previously unknown whether it was possible for a policy to be strongly asymptotically optimal in the class of all computable probabilistic environments. Our agent, Inquisitive Reinforcement Learner (Inq), is more likely to explore the more it expects an exploratory action to reduce its uncertainty about which environment it is in, hence the term inquisitive. Exploring inquisitively is a strategy that can be applied generally; for more manageable environment classes, inquisitiveness is tractable. We conducted experiments in "grid-worlds" to compare the Inquisitive Reinforcement Learner to other weakly asymptotically optimal agents.