ABodyBuilder3: Improved and scalable antibody structure predictions

Accurate prediction of antibody structure is a central task in the design and development of monoclonal antibodies, notably to understand both their developability and their binding properties. In this article, we introduce ABodyBuilder3, an improved and scalable antibody structure prediction model based on ImmuneBuilder. We achieve a new state-of-the-art accuracy in the modelling of CDR loops by leveraging language model embeddings, and show how predicted structures can be further improved through careful relaxation strategies. Finally, we incorporate a predicted Local Distance Difference Test into the model output to allow for a more accurate estimation of uncertainties.

Large scale paired antibody language models

Antibodies are proteins produced by the immune system that can identify and neutralise a wide variety of antigens with high specificity and affinity, and constitute the most successful class of biotherapeutics. With the advent of next-generation sequencing, billions of antibody sequences have been collected in recent years, though their application in the design of better therapeutics has been constrained by the sheer volume and complexity of the data. To address this challenge, we present IgBert and IgT5, the best performing antibody-specific language models developed to date which can consistently handle both paired and unpaired variable region sequences as input. These models are trained comprehensively using the more than two billion unpaired sequences and two million paired sequences of light and heavy chains present in the Observed Antibody Space dataset. We show that our models outperform existing antibody and protein language models on a diverse range of design and regression tasks relevant to antibody engineering. This advancement marks a significant leap forward in leveraging machine learning, large scale data sets and high-performance computing for enhancing antibody design for therapeutic development.

Inverse folding for antibody sequence design using deep learning

We consider the problem of antibody sequence design given 3D structural information. Building on previous work, we propose a fine-tuned inverse folding model that is specifically optimised for antibody structures and outperforms generic protein models on sequence recovery and structure robustness when applied on antibodies, with notable improvement on the hypervariable CDR-H3 loop. We study the canonical conformations of complementarity-determining regions and find improved encoding of these loops into known clusters. Finally, we consider the applications of our model to drug discovery and binder design and evaluate the quality of proposed sequences using physics-based methods.

Structure-Aware Robustness Certificates for Graph Classification

Certifying the robustness of a graph-based machine learning model poses a critical challenge for safety. Current robustness certificates for graph classifiers guarantee output invariance with respect to the total number of node pair flips (edge addition or edge deletion), which amounts to an $l_{0}$ ball centred on the adjacency matrix. Although theoretically attractive, this type of isotropic structural noise can be too restrictive in practical scenarios where some node pairs are more critical than others in determining the classifier's output. The certificate, in this case, gives a pessimistic depiction of the robustness of the graph model. To tackle this issue, we develop a randomised smoothing method based on adding an anisotropic noise distribution to the input graph structure. We show that our process generates structural-aware certificates for our classifiers, whereby the magnitude of robustness certificates can vary across different pre-defined structures of the graph. We demonstrate the benefits of these certificates in both synthetic and real-world experiments.

Bayesian Optimisation of Functions on Graphs

The increasing availability of graph-structured data motivates the task of optimising over functions defined on the node set of graphs. Traditional graph search algorithms can be applied in this case, but they may be sample-inefficient and do not make use of information about the function values; on the other hand, Bayesian optimisation is a class of promising black-box solvers with superior sample efficiency, but it has been scarcely been applied to such novel setups. To fill this gap, we propose a novel Bayesian optimisation framework that optimises over functions defined on generic, large-scale and potentially unknown graphs. Through the learning of suitable kernels on graphs, our framework has the advantage of adapting to the behaviour of the target function. The local modelling approach further guarantees the efficiency of our method. Extensive experiments on both synthetic and real-world graphs demonstrate the effectiveness of the proposed optimisation framework.

Graph similarity learning for change-point detection in dynamic networks

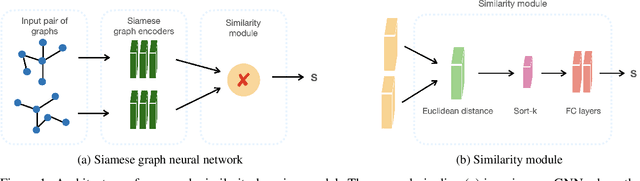
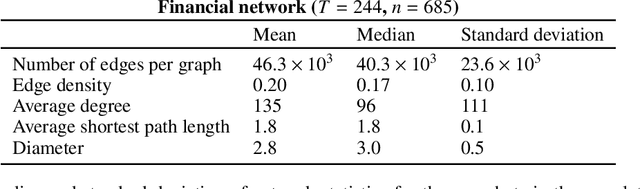
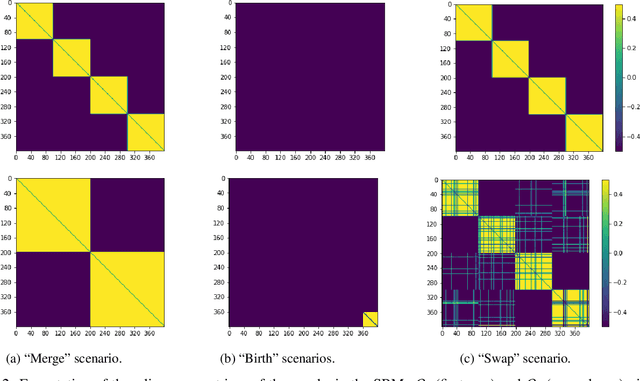
Dynamic networks are ubiquitous for modelling sequential graph-structured data, e.g., brain connectome, population flows and messages exchanges. In this work, we consider dynamic networks that are temporal sequences of graph snapshots, and aim at detecting abrupt changes in their structure. This task is often termed network change-point detection and has numerous applications, such as fraud detection or physical motion monitoring. Leveraging a graph neural network model, we design a method to perform online network change-point detection that can adapt to the specific network domain and localise changes with no delay. The main novelty of our method is to use a siamese graph neural network architecture for learning a data-driven graph similarity function, which allows to effectively compare the current graph and its recent history. Importantly, our method does not require prior knowledge on the network generative distribution and is agnostic to the type of change-points; moreover, it can be applied to a large variety of networks, that include for instance edge weights and node attributes. We show on synthetic and real data that our method enjoys a number of benefits: it is able to learn an adequate graph similarity function for performing online network change-point detection in diverse types of change-point settings, and requires a shorter data history to detect changes than most existing state-of-the-art baselines.

On the Unreasonable Effectiveness of Feature propagation in Learning on Graphs with Missing Node Features

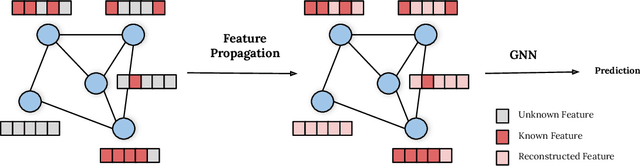
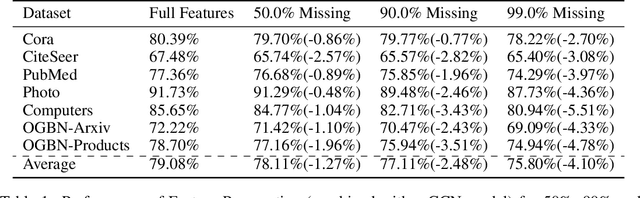
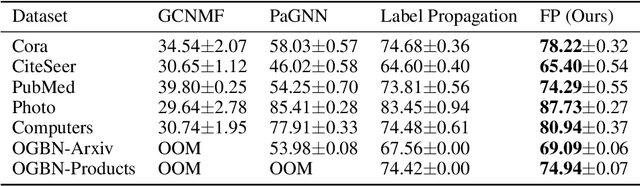
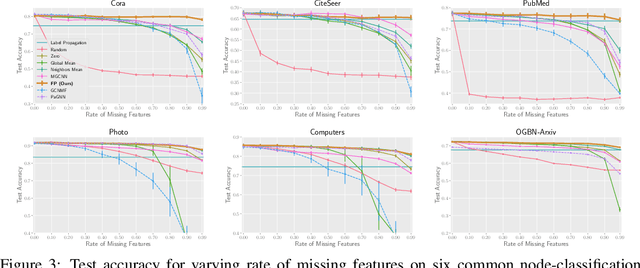
While Graph Neural Networks (GNNs) have recently become the de facto standard for modeling relational data, they impose a strong assumption on the availability of the node or edge features of the graph. In many real-world applications, however, features are only partially available; for example, in social networks, age and gender are available only for a small subset of users. We present a general approach for handling missing features in graph machine learning applications that is based on minimization of the Dirichlet energy and leads to a diffusion-type differential equation on the graph. The discretization of this equation produces a simple, fast and scalable algorithm which we call Feature Propagation. We experimentally show that the proposed approach outperforms previous methods on seven common node-classification benchmarks and can withstand surprisingly high rates of missing features: on average we observe only around 4% relative accuracy drop when 99% of the features are missing. Moreover, it takes only 10 seconds to run on a graph with $\sim$2.5M nodes and $\sim$123M edges on a single GPU.

Adversarial Attacks on Graph Classification via Bayesian Optimisation

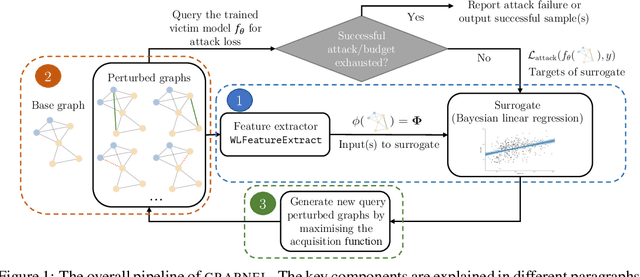
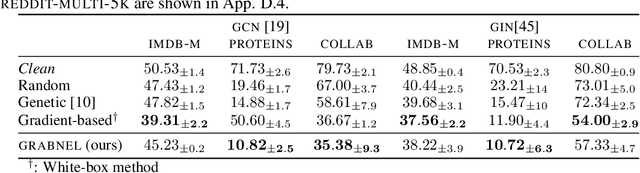
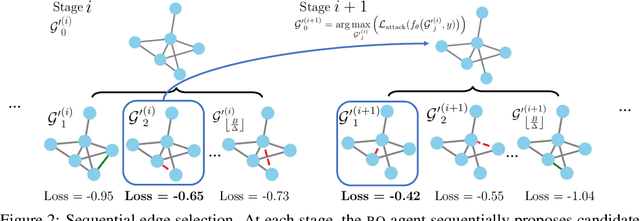
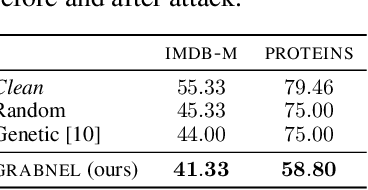
Graph neural networks, a popular class of models effective in a wide range of graph-based learning tasks, have been shown to be vulnerable to adversarial attacks. While the majority of the literature focuses on such vulnerability in node-level classification tasks, little effort has been dedicated to analysing adversarial attacks on graph-level classification, an important problem with numerous real-life applications such as biochemistry and social network analysis. The few existing methods often require unrealistic setups, such as access to internal information of the victim models, or an impractically-large number of queries. We present a novel Bayesian optimisation-based attack method for graph classification models. Our method is black-box, query-efficient and parsimonious with respect to the perturbation applied. We empirically validate the effectiveness and flexibility of the proposed method on a wide range of graph classification tasks involving varying graph properties, constraints and modes of attack. Finally, we analyse common interpretable patterns behind the adversarial samples produced, which may shed further light on the adversarial robustness of graph classification models.

Interpretable Stability Bounds for Spectral Graph Filters

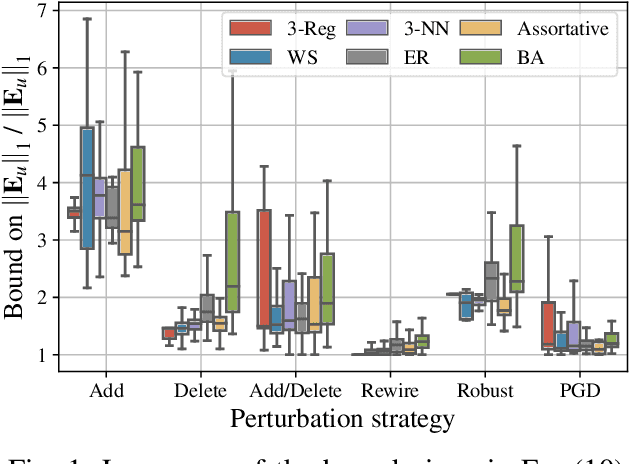
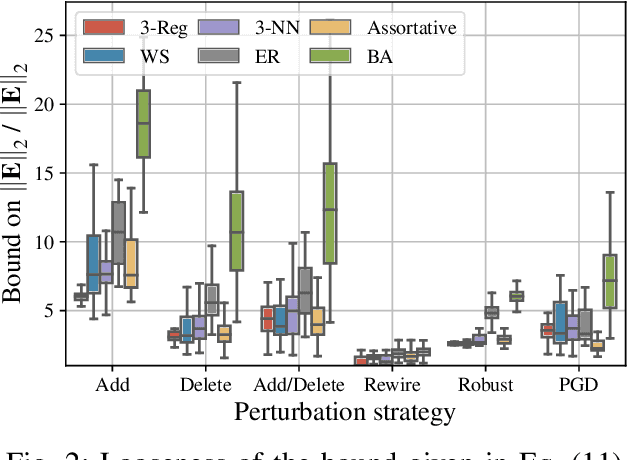
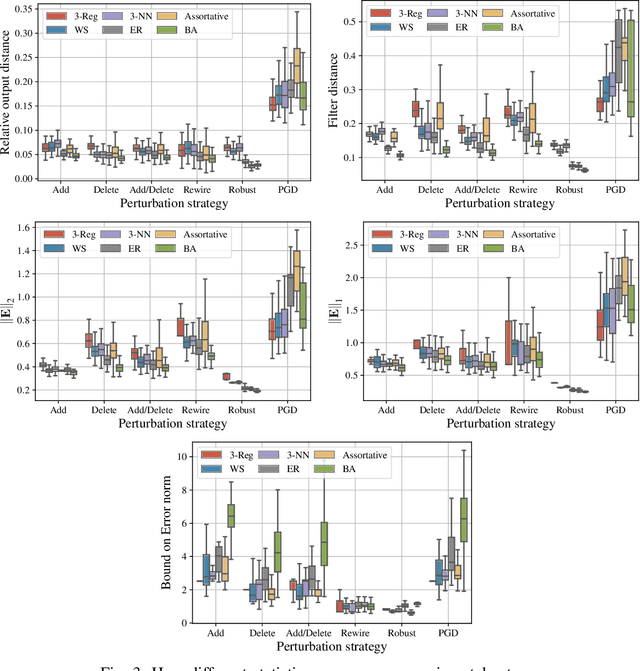
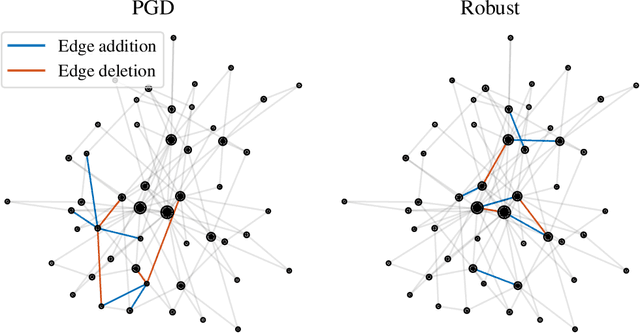
Graph-structured data arise in a variety of real-world context ranging from sensor and transportation to biological and social networks. As a ubiquitous tool to process graph-structured data, spectral graph filters have been used to solve common tasks such as denoising and anomaly detection, as well as design deep learning architectures such as graph neural networks. Despite being an important tool, there is a lack of theoretical understanding of the stability properties of spectral graph filters, which are important for designing robust machine learning models. In this paper, we study filter stability and provide a novel and interpretable upper bound on the change of filter output, where the bound is expressed in terms of the endpoint degrees of the deleted and newly added edges, as well as the spatial proximity of those edges. This upper bound allows us to reason, in terms of structural properties of the graph, when a spectral graph filter will be stable. We further perform extensive experiments to verify intuition that can be gained from the bound.

On the Stability of Graph Convolutional Neural Networks under Edge Rewiring

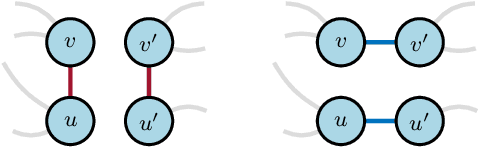
Graph neural networks are experiencing a surge of popularity within the machine learning community due to their ability to adapt to non-Euclidean domains and instil inductive biases. Despite this, their stability, i.e., their robustness to small perturbations in the input, is not yet well understood. Although there exists some results showing the stability of graph neural networks, most take the form of an upper bound on the magnitude of change due to a perturbation in the graph topology. However, these existing bounds tend to be expressed in terms of uninterpretable variables, limiting our understanding of the model robustness properties. In this work, we develop an interpretable upper bound elucidating that graph neural networks are stable to rewiring between high degree nodes. This bound and further research in bounds of similar type provide further understanding of the stability properties of graph neural networks.