Max Welling
UC Irvine
Amortized Causal Discovery: Learning to Infer Causal Graphs from Time-Series Data
Jun 18, 2020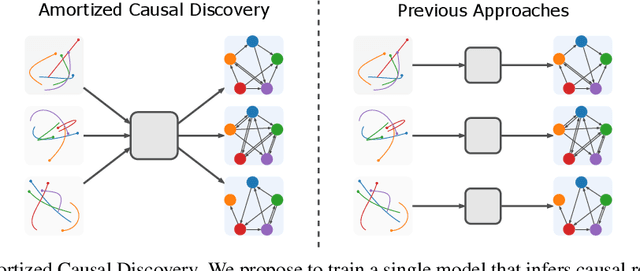
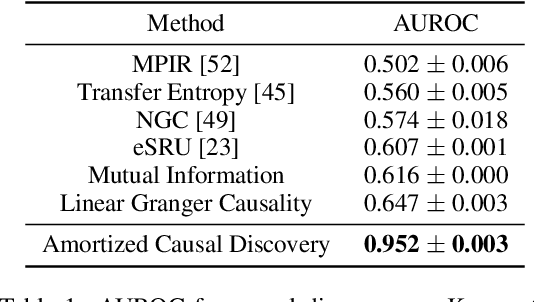
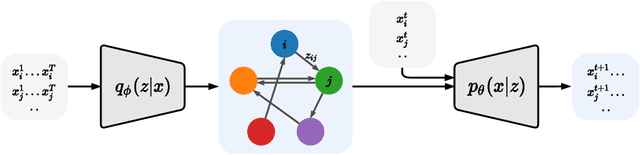
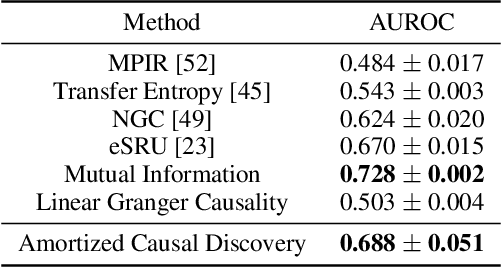
Abstract:Standard causal discovery methods must fit a new model whenever they encounter samples from a new underlying causal graph. However, these samples often share relevant information - for instance, the dynamics describing the effects of causal relations - which is lost when following this approach. We propose Amortized Causal Discovery, a novel framework that leverages such shared dynamics to learn to infer causal relations from time-series data. This enables us to train a single, amortized model that infers causal relations across samples with different underlying causal graphs, and thus makes use of the information that is shared. We demonstrate experimentally that this approach, implemented as a variational model, leads to significant improvements in causal discovery performance, and show how it can be extended to perform well under hidden confounding.
The Convolution Exponential and Generalized Sylvester Flows
Jun 02, 2020
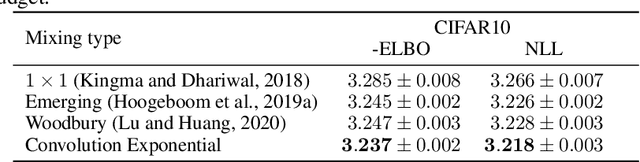

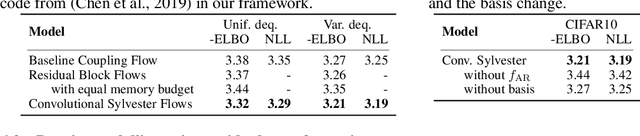
Abstract:This paper introduces a new method to build linear flows, by taking the exponential of a linear transformation. This linear transformation does not need to be invertible itself, and the exponential has the following desirable properties: it is guaranteed to be invertible, its inverse is straightforward to compute and the log Jacobian determinant is equal to the trace of the linear transformation. An important insight is that the exponential can be computed implicitly, which allows the use of convolutional layers. Using this insight, we develop new invertible transformations named convolution exponentials and graph convolution exponentials, which retain the equivariance of their underlying transformations. In addition, we generalize Sylvester Flows and propose Convolutional Sylvester Flows which are based on the generalization and the convolution exponential as basis change. Empirically, we show that the convolution exponential outperforms other linear transformations in generative flows on CIFAR10 and the graph convolution exponential improves the performance of graph normalizing flows. In addition, we show that Convolutional Sylvester Flows improve performance over residual flows as a generative flow model measured in log-likelihood.
Bayesian Bits: Unifying Quantization and Pruning
May 15, 2020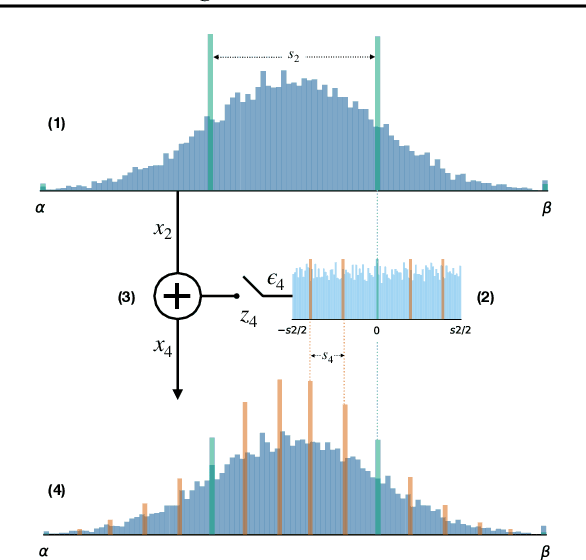
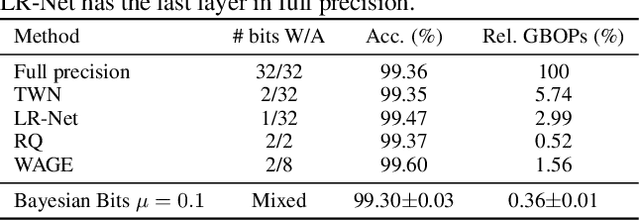
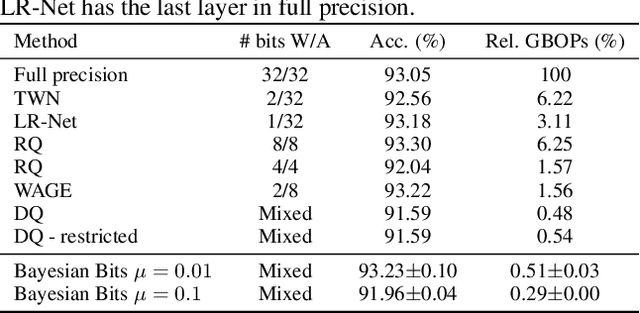
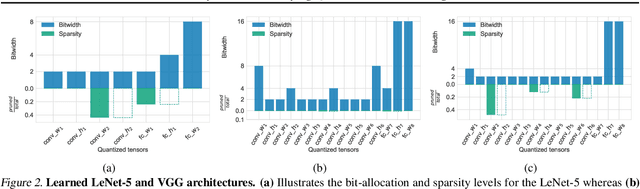
Abstract:We introduce Bayesian Bits, a practical method for joint mixed precision quantization and pruning through gradient based optimization. Bayesian Bits employs a novel decomposition of the quantization operation, which sequentially considers doubling the bit width. At each new bit width, the residual error between the full precision value and the previously rounded value is quantized. We then decide whether or not to add this quantized residual error for a higher effective bit width and lower quantization noise. By starting with a power-of-two bit width, this decomposition will always produce hardware-friendly configurations, and through an additional 0-bit option, serves as a unified view of pruning and quantization. Bayesian Bits then introduces learnable stochastic gates, which collectively control the bit width of the given tensor. As a result, we can obtain low bit solutions by performing approximate inference over the gates, with prior distributions that encourage most of them to be switched off. We further show that, under some assumptions, L0 regularization of the network parameters corresponds to a specific instance of the aforementioned framework. We experimentally validate our proposed method on several benchmark datasets and show that we can learn pruned, mixed precision networks that provide a better trade-off between accuracy and efficiency than their static bit width equivalents.
A Data and Compute Efficient Design for Limited-Resources Deep Learning
Apr 21, 2020


Abstract:Thanks to their improved data efficiency, equivariant neural networks have gained increased interest in the deep learning community. They have been successfully applied in the medical domain where symmetries in the data can be effectively exploited to build more accurate and robust models. To be able to reach a much larger body of patients, mobile, on-device implementations of deep learning solutions have been developed for medical applications. However, equivariant models are commonly implemented using large and computationally expensive architectures, not suitable to run on mobile devices. In this work, we design and test an equivariant version of MobileNetV2 and further optimize it with model quantization to enable more efficient inference. We achieve close-to state of the art performance on the Patch Camelyon (PCam) medical dataset while being more computationally efficient.
Guided Variational Autoencoder for Disentanglement Learning
Apr 02, 2020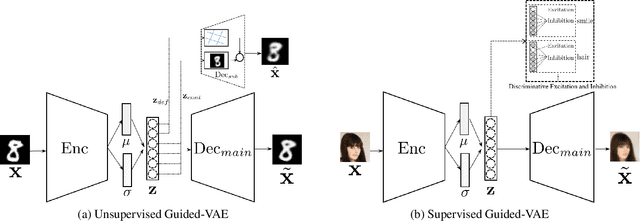
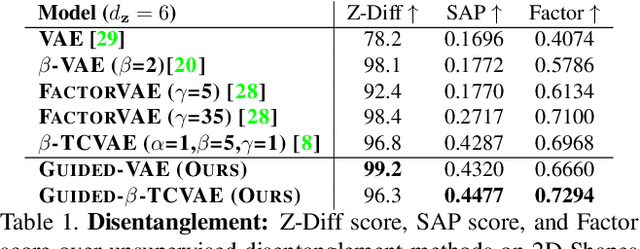

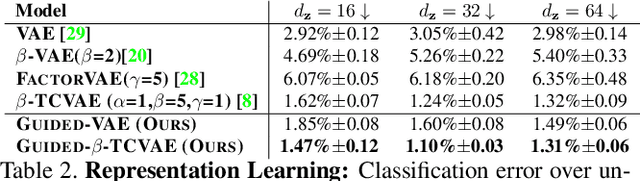
Abstract:We propose an algorithm, guided variational autoencoder (Guided-VAE), that is able to learn a controllable generative model by performing latent representation disentanglement learning. The learning objective is achieved by providing signals to the latent encoding/embedding in VAE without changing its main backbone architecture, hence retaining the desirable properties of the VAE. We design an unsupervised strategy and a supervised strategy in Guided-VAE and observe enhanced modeling and controlling capability over the vanilla VAE. In the unsupervised strategy, we guide the VAE learning by introducing a lightweight decoder that learns latent geometric transformation and principal components; in the supervised strategy, we use an adversarial excitation and inhibition mechanism to encourage the disentanglement of the latent variables. Guided-VAE enjoys its transparency and simplicity for the general representation learning task, as well as disentanglement learning. On a number of experiments for representation learning, improved synthesis/sampling, better disentanglement for classification, and reduced classification errors in meta-learning have been observed.
Gauge Equivariant Mesh CNNs: Anisotropic convolutions on geometric graphs
Mar 11, 2020

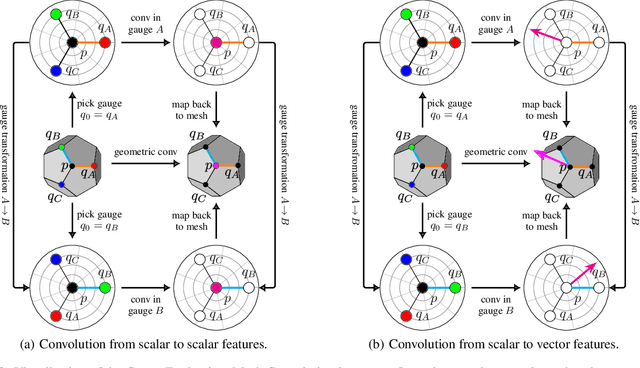
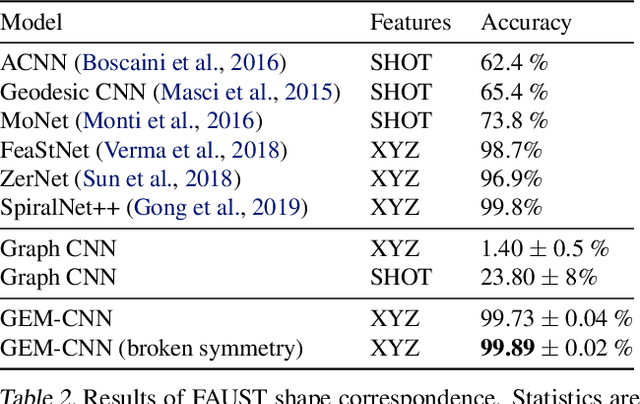
Abstract:A common approach to define convolutions on meshes is to interpret them as a graph and apply graph convolutional networks (GCNs). Such GCNs utilize isotropic kernels and are therefore insensitive to the relative orientation of vertices and thus to the geometry of the mesh as a whole. We propose Gauge Equivariant Mesh CNNs which generalize GCNs to apply anisotropic gauge equivariant kernels. Since the resulting features carry orientation information, we introduce a geometric message passing scheme defined by parallel transporting features over mesh edges. Our experiments validate the significantly improved expressivity of the proposed model over conventional GCNs and other methods.
Neural Enhanced Belief Propagation on Factor Graphs
Mar 04, 2020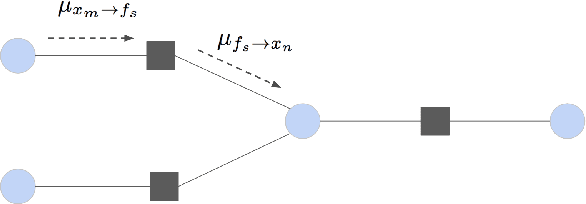
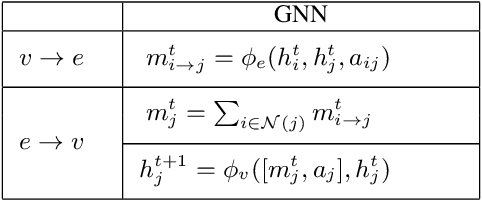
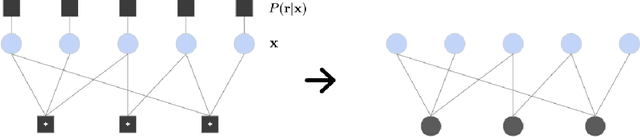
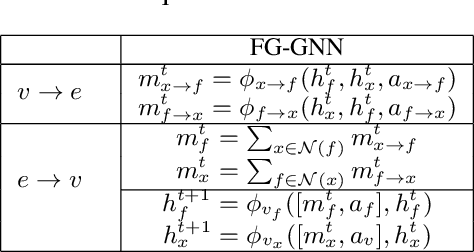
Abstract:A graphical model is a structured representation of locally dependent random variables. A traditional method to reason over these random variables is to perform inference using belief propagation. When provided with the true data generating process, belief propagation can infer the optimal posterior probability estimates in tree structured factor graphs. However, in many cases we may only have access to a poor approximation of the data generating process, or we may face loops in the factor graph, leading to suboptimal estimates. In this work we first extend graph neural networks to factor graphs (FG-GNN). We then propose a new hybrid model that runs conjointly a FG-GNN with belief propagation. The FG-GNN receives as input messages from belief propagation at every inference iteration and outputs a corrected version of them. As a result, we obtain a more accurate algorithm that combines the benefits of both belief propagation and graph neural networks. We apply our ideas to error correction decoding tasks, and we show that our algorithm can outperform belief propagation for LDPC codes on bursty channels.
Plannable Approximations to MDP Homomorphisms: Equivariance under Actions
Feb 27, 2020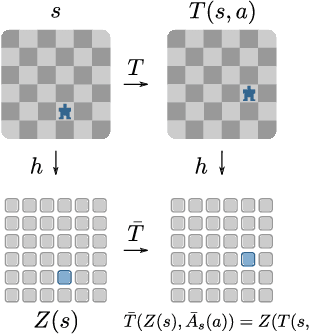
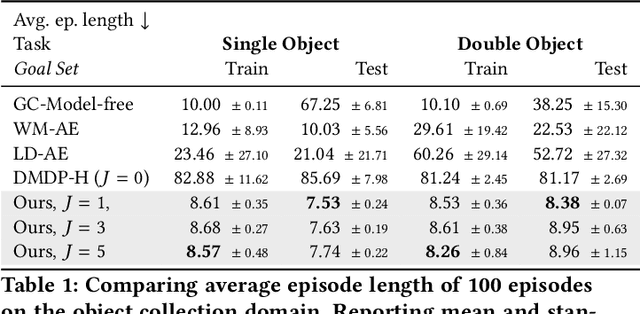
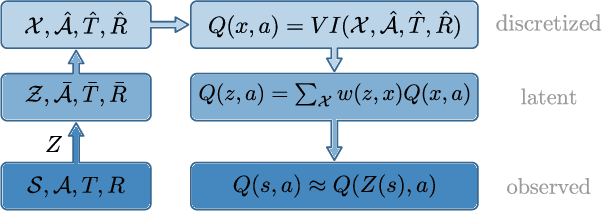
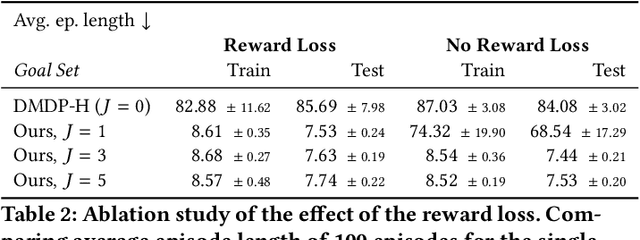
Abstract:This work exploits action equivariance for representation learning in reinforcement learning. Equivariance under actions states that transitions in the input space are mirrored by equivalent transitions in latent space, while the map and transition functions should also commute. We introduce a contrastive loss function that enforces action equivariance on the learned representations. We prove that when our loss is zero, we have a homomorphism of a deterministic Markov Decision Process (MDP). Learning equivariant maps leads to structured latent spaces, allowing us to build a model on which we plan through value iteration. We show experimentally that for deterministic MDPs, the optimal policy in the abstract MDP can be successfully lifted to the original MDP. Moreover, the approach easily adapts to changes in the goal states. Empirically, we show that in such MDPs, we obtain better representations in fewer epochs compared to representation learning approaches using reconstructions, while generalizing better to new goals than model-free approaches.
Gradient $\ell_1$ Regularization for Quantization Robustness
Feb 18, 2020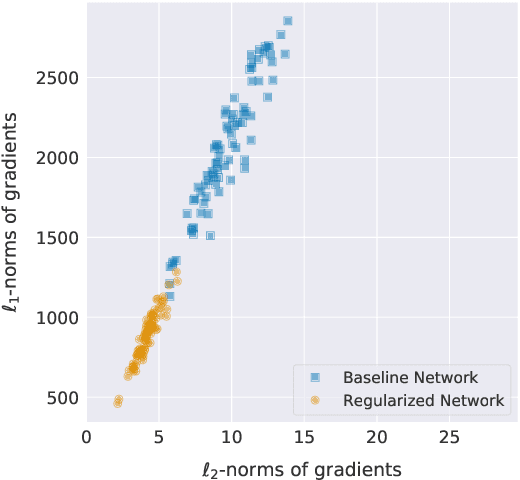
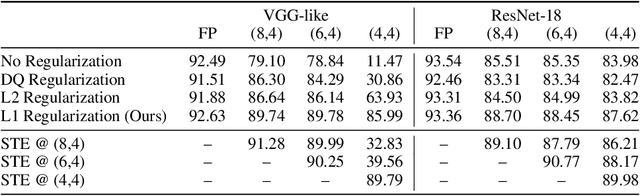
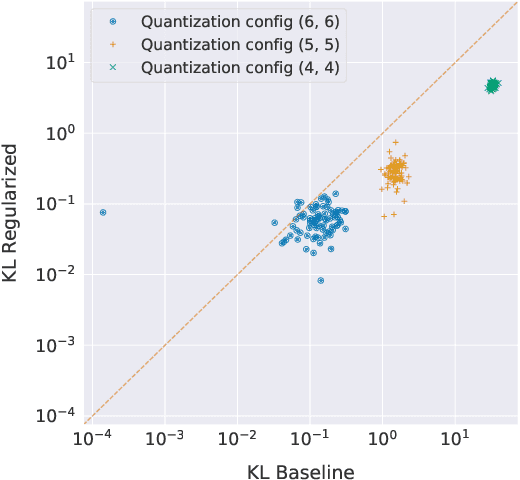
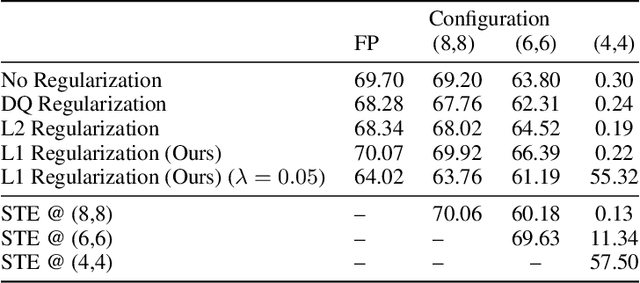
Abstract:We analyze the effect of quantizing weights and activations of neural networks on their loss and derive a simple regularization scheme that improves robustness against post-training quantization. By training quantization-ready networks, our approach enables storing a single set of weights that can be quantized on-demand to different bit-widths as energy and memory requirements of the application change. Unlike quantization-aware training using the straight-through estimator that only targets a specific bit-width and requires access to training data and pipeline, our regularization-based method paves the way for "on the fly'' post-training quantization to various bit-widths. We show that by modeling quantization as a $\ell_\infty$-bounded perturbation, the first-order term in the loss expansion can be regularized using the $\ell_1$-norm of gradients. We experimentally validate the effectiveness of our regularization scheme on different architectures on CIFAR-10 and ImageNet datasets.
Estimating Gradients for Discrete Random Variables by Sampling without Replacement
Feb 14, 2020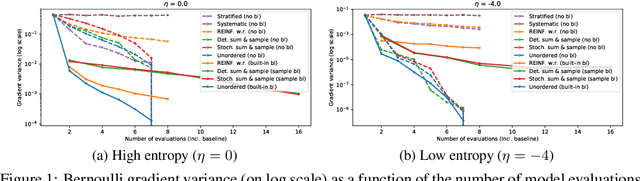
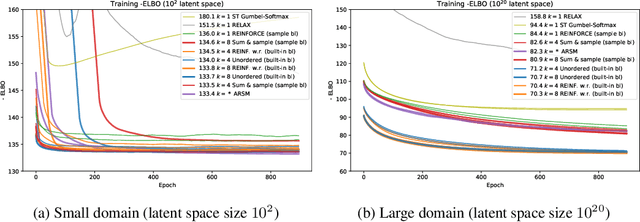
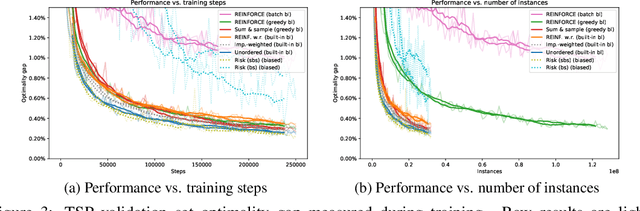
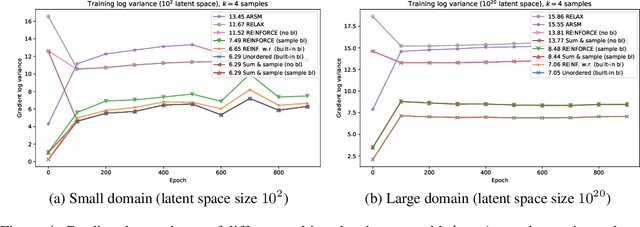
Abstract:We derive an unbiased estimator for expectations over discrete random variables based on sampling without replacement, which reduces variance as it avoids duplicate samples. We show that our estimator can be derived as the Rao-Blackwellization of three different estimators. Combining our estimator with REINFORCE, we obtain a policy gradient estimator and we reduce its variance using a built-in control variate which is obtained without additional model evaluations. The resulting estimator is closely related to other gradient estimators. Experiments with a toy problem, a categorical Variational Auto-Encoder and a structured prediction problem show that our estimator is the only estimator that is consistently among the best estimators in both high and low entropy settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge